Transformer 中self-attention以及mask操作的原理以及代码解析
笔者最近在梳理自然语言预训练模型的有关内容。在看到Bert的时候,突然发现Bert之后的预训练模型都与Transformer结构有关。该结构的一个为人所知的重点是self-attention,但是其另外一个重点mask操作却被人了解的很少,笔者借鉴了其他博主的优质内容,加上自己的理解整理了一下,希望从原理以及代码的角度来学习一下这两个知识点。
**
self-attention
**
Self-attention可以说是整个Transformer模型的核心思想。本章关于Self-attention的公式图片均来源于Vaswani 的文章attention is all you need以及博主adam-liu 的图解Transformer,或者本人手绘.该篇博客在Self-attention的讲述上非常精彩,建议初学者去看一下其原博客内容。
self-attention的出现是为了摆脱循环神经网络不能并行计算的缺点而提出的,它的设计模式可以通过当前单词去查看其输入序列中的其他单词,以此来寻找编码这个单词更好的线索。
在学习Self-Attention的过程中,首先学习的是一个attention的普遍形式(文章中称之为Scaled Dot-Product Attention),看过Attention is all your need 文章的同学肯定知道其计算其计算方式就是通过构造三个矩阵Q,K,V来计算Scaled Dot-Product Attention矩阵,具体的计算流程以及以及计算公式如下图所示:
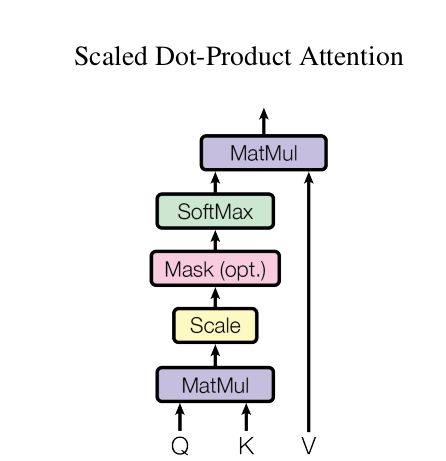
图1 Scaled Dot-Product Attention
Vaswani文章第一次对attention提出了一个归纳化的公式。在NMT领域当中,我们对比传统attention的计算方式,很容易看出以上Q是来源于Encoder端的隐藏层状态,而K,V是来源于Decoder端的隐藏曾状态。
而Transformer使用的Self-attention。顾名思义即句子中的每一个词都要和该句子当中的所有词进行一个attention计算,目的是学习句子内部的词依赖关系,获取词的内部结构。因此,从这个特点当中我们可以其实也能推测出Self-attention计算的信息来源都是来源于其句子本身。
故在上述attention的计算公式当中,可以看出self-attention即Q=K=V。下面用Transformer的部分代码(Tensorflow)来进一步的了解Q,K,V在self-attention中的构成(以Encoder端为例)。
以下是train.py的部分代码
1 with tf.variable_scope("num_blocks_{}".format(i)):
2 self.enc = multihead_attention(queries=self.enc,
3 keys=self.enc,
4 num_units=hp.hidden_units,
5 num_heads=hp.num_heads,
6 dropout_rate=hp.dropout_rate,
7 is_traing=is_traing,
8 causality=False)
以下是module.py的部分代码
1 def multihead_attention(queries,
2 keys,
3 num_units=None,
4 num_heads=8,
5 dropout_rate=0,
6 is_training=True,
7 causality=False,
8 scope='multihead_attention',
9 reuse=None):
10
11 with tf.variable_scope(scope,reuse=reuse):
12 if num_units is None:
13 num_units = queries.get_shape().as_list[-1]
14
15 Q = tf.layers.dense(queries,num_units,activation=tf.nn.relu)
16 K = tf.layers.dense(keys,num_units,activation=tf.nn.relu)
17 V = tf.layers.dense(keys,num_units,activation=tf.nn.relu)
train.py中的 self.enc代表的就是 encoder端经过word_embedding以及position_embedding之后的句子信息,之后用X来代替。
根据其传入 multihead_attention 函数中的参数来看,在机器翻译领域当中,Transformer当中的queries以及Keys都是其输入信息x。
而在module.py文件当中,我们从矩阵Q,K,V的计算公式中我们可以发现:
Q是将queries输入进一个节点数为num_units的前馈神经网络之后得到的矩阵
而K,V则是将keys输入进一个节点数为num_units的前馈神经网络之后得到的矩阵。
结合所有的信息,在机器翻译领域当中,Q,K,V的所有来源就是encoder端的输入X。即可以看成Q=K=V
具体计算过程如下图所示:

图3K,Q,V的计算过程
从图中我们可发现,当中使用了三个权重矩阵(WQ,WK,WV)来右乘输入信息矩阵X获得K,Q,V。之后我们便可以使用上述的attention公式来计算self-attention的矩阵。
在这里也顺便提一下muilti_head的概念,Multi_head self_attention的意思就是重复以上过程多次,论文当中是重复8次,即8个Head,使用多套(WQ,WK,WV)矩阵(只要在初始化的时候多稍微变一下,很容易获得多套权重矩阵)。获得多套(Q,K,V)矩阵,然后进行attention计算时便能获得多个self_attention矩阵。
self-attention之后紧接着的步骤是前馈神经网络,而前馈神经网络接受的是单个的矩阵向量,而不是多个矩阵,因此需要把计算得到的多个self-attention矩阵采用某种方式进行合并。因此文章中给出的思路是将这多个连接在一起(可能是简单就是好,No free lunch原则)再和一个矩阵W0相乘。步骤如下图:
图四multi_head_attention的合并过程
综合上述说法,multi_layer_self-attention的整体计算流程如下图所示:

图5multi_head_self_attention的整体计算流程
self-attention在神经机器翻译实际的操作设计当中,不仅仅是由上面self-attention计算公式那般设计,其中还要加入Mask操作。
其中在Encoder端和Decoder端都需要使用的Mask操作,称之为PADDING MASK。
而仅仅在Decoder段使用的Mask操作,则被称之为Sequence MASK。下面将结合代码分别对其进行介绍。
PADDING MASK
我们在训练的过程中,自然语言数据往往都是以Batch的形式输入进的模型,而一个batch中的每一句话不能保证长度都是一样的,所以需要使用PADDING的方式将所有的句子都补全到最长的长度,比如拿0进行填充,但是我们知道这种用0填充的位置的信息是完全没有意义的,因此我们希望这个位置不参与后期的反向传播过程。以此避免最后影响模型自身的效果,因此提出了在训练时将补全的位置给Mask掉的做法。而在Self-attention的计算当中,我们自然也不希望有效词的注意力集中在这些没有意义的位置上,因此使用了PADDING MASK的方式.
PADDING MASK在attention的计算过程中处于softmax之前(图1中的opt表示optional即该层可加可不加,若是不想使用PADDING MASK操作,则直接Softmax就完事了),通过PADDING MASK的操作,使得补全位置上的值成为一个非常大的负数(可以是负无穷),这样的话,经过Softmax层的时候,这些位置上的概率就是0。以此操作就相当于把补全位置的无用信息给遮蔽掉了(Mask掉了)。具体操作见如下代码(请和注释一起食用):
def multihead_attention(queries,
keys,
num_units=None,
num_heads=8,
dropout_rate=0,
is_traing=True,
causality=False,
scope='multihead_attention',
reuse=None):
with tf.variable_scope(scope,reuse=reuse):
if num_units is None:
num_units = queries.get_shape().as_list[-1]
# Q,K,V的shape均为(batch_size,max_length,hidden_size)
Q = tf.layers.dense(queries,num_units,activation=tf.nn.relu)
K = tf.layers.dense(keys,num_units,activation=tf.nn.relu)
V = tf.layers.dense(keys,num_units,activation=tf.nn.relu)
#通过tf.split将Q,K,按照最后一维切分成num_heads份,然后按第一维度进行拼接,
#以此达到“多头的效果”,此时的Q_就相当于num_heads个Q的拼接,其余同理。
Q_ = tf.concat(tf.split(Q,num_heads,axis=2),axis=0)
K_ = tf.concat(tf.split(K,num_heads,axis=2),axis=0)
V_ = tf.concat(tf.split(V,num_heads,axis=2),axis=0)
#这便是图2公式中SoftMax部分的内容
A = tf.transpose(K_,[0,2,1])
outputs = tf.matmul(Q_,tf.transpose(K_,[0,2,1]))
outputs = outputs / (K_.get_shape().as_list()[-1]**0.5)
#以下是PADDING MASK的过程 不管是在Encoder的计算中还是Decoder的计算当中都会使用。
#这个是整个PADDING MASK的核心知识点,当输入的自然语言句子转换成embedding向量的时候.
#若embedding的时候,将用0填充的位置(PADDING)进行embedding的时候全部使用0来代替:
# 举个例子:若一句自然语言用0填充之后的表示方式为[1,2,0,0],若embedding_size选择为2
# vocab_size为3.我们的lookup_table则初始化为如下的一个3*3的矩阵(第一行必须全部为0):
# [[0,0,0],
# [-0.12,0.21,0.32],
# [0.14,0.24,-0.32]]
# 那么经过tf.nn.embedding_lookup()之后 原自然语言句子就被embedding变成了如下形式
# [1,2,0,0]->[[-0.12,0.21,0.32],
# [0.14,0.24,-0.32],
# [0,0,0],
# [0,0,0]]
# 这样的话,通过如下的这几步的操作,便能将与key_masks为0的位置(即填充的位置)一样的output的位置变成一个特别小的一个负数.
# 这样,经过后期的Softmax的时候,便能将该填充位置的输出变成0,以此来防止因为填充位置的无用信息影响模型的效果
# 如果在最开始的embedding的同时没有使用0元素进行遮盖(即lookup_table矩阵第一行不为0,而是一些别的随机数)
# 那么PADDING_MASK将不起作用.
key_masks = tf.sign(tf.abs(tf.reduce_sum(keys, axis=-1)))
#接下来的两步操作只是为了能够让key_masks的维度能够和outputs匹配
key_masks = tf.tile(key_masks, [num_heads, 1])
key_masks = tf.tile(tf.expand_dims(key_masks, 1), [1, tf.shape(queries)[1], 1])
# paddings里面的值都是非常小的负数,当key_masks矩阵的某个变量和0相等的时候,将同样位置上的outputs的值变成一个特别小的数.
paddings = tf.ones_like(outputs)*(-2**32+1)
outputs = tf.where(tf.equal(key_masks, 0), paddings, outputs)
outputs = tf.nn.softmax(outputs)
query_masks = tf.sign(tf.abs(tf.reduce_sum(queries,axis=-1)))
query_masks = tf.tile(query_masks,[num_heads,1])
query_masks = tf.tile(tf.expand_dims(query_masks,-1),[1,1,tf.shape(keys)[1]])
outputs *= query_masks
在进行softmax之后,源码当中又加入了一个query_mask.其实这里我是有点没太懂的,在这儿搬运一下其他博主说的话,若是有能理解的同学可以留言:原因在于若不是self-attention的情况下,query和key的第二维可能不同(两者句子长度不同)可能会出现一个填充,一个没有填充的状况出现,因此需要分情况讨论.但是keys_mask和query_mask都是一样的目的.
以上便是PADDING_MASK的理论解释以及在实际中的运用方法.
Sequence MASK
Sequence Mask只在Decoder端进行,目的是为了使得decoder不能看见未来的信息.也就是对于一个序列中的第i个token,解码的时候只能够依靠i时刻之前(包括i)的的输出,而不能依赖于i时刻之后的输出.因此我们要采取一个遮盖的方法(Mask)使得其在计算self-attention的时候只用i个时刻之前的token进行计算,因为Decoder是用来做预测的,而在训练预测能力的时候,我们不能够"提前看答案",因此要将未来的信息给遮盖住.效果如下图所示:

图6 mask之后的self-attention矩阵图
图中灰色部分即为mask的部分.实际操作的代码如图所示,再次强调,sequence mask 操作只发生在decoder阶段,而且对于self-attenion而言,这是一个必要的操作,不像之前的PADDING_MASK可以选择跳过:
# 这遮盖的方法和之前的PADDING_MASK的操作方法基本一致,不一样的只是masks矩阵中的元素不一样,masks矩阵是一个
#下三角矩阵,即对角线以及对角线一下是1,对角线以上全为0.之后同样将outputs位置对于Masks矩阵为0的位置上的元素统统
#替换成一个很小的负数,这样之后在经过softmax的时候就能够将mask部分的self-attention的计算值变成0.以此来达到遮盖
#未来信息的目的
diag_vals = tf.ones_like(outputs[0, :, :])
tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense()
masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(outputs)[0], 1, 1])
paddings = tf.ones_like(masks)*(-2**32+1)
outputs = tf.where(tf.equal(masks, 0), paddings, outputs)
如果有能够来讨论交流的小伙伴欢迎在下面留言!!!好好学习天天向上!
