深度学习基础（2）——分类与回归，评价指标的设置

概述

分类算法和回归算法是对真实世界不同建模的方法。

• 分类方法是一种对离散型随机变量建模或预测的监督学习算法。其输出是离散的，例如大自然的生物种类划分，邮件分类等。
• 回归方法是一种对数值型连续随机变量进行预测和建模的监督学习算法。其输出是连续的，包括房价预测、股票走势等连续变化的案例。

分类的目的是找到决策边界，回归的目的是找到最优拟合。因此，在实际建模过程时，采用分类模型还是回归模型，取决于你对任务（真实世界）的分析和理解。

分类算法

分类问题的关键在于分类模型经过训练之后能否对新的输入样本进行类别预测。且分类算法的输出是有限个离散值。

常用算法

算法	优点	缺点
神经网络（Neural Network）	1）分类准确率高，效果好。 2）并行处理能力强。 3）分布式存储和学习能力强。 4）鲁棒性较强，不易受噪声影响。	1）需要大量参数（网络拓扑、阀值、阈值）。 2）训练时间过长。
贝叶斯分类法（Bayes ）	1）所需估计的参数少，对于缺失数据不敏感。 2）分类效率稳定。	1）需要假设属性之间相互独立，条件苛刻。 2）需要知道先验概率。 3）分类决策存在一定的错误率。
决策树（Decision Tree）	1）不需要任何领域知识或参数假设。 2）适合高维数据。 3）简单易于理解。 4）短时间内处理大量数据，得到可行且效果较好的结果。 5）能够同时处理数据型和常规性属性。	1）对于各类别样本数量不一致数据，信息增益偏向于那些具有更多数值的特征。 2）易于过拟合。 3）忽略属性之间的相关性。 4）不支持在线学习。
K近邻	1）理论比较成熟，既可以用来做分类也可以用来做回归； 2）可用于非线性分类； 3）训练时间复杂度为O(n)； 4）准确度高，对数据没有假设，对outlier不敏感；	1）计算量太大。 2）对于样本分类不均衡的问题，会产生误判。 3）需要大量的内存。 4）输出的可解释性不强。
逻辑回归（Logistic Regression）	1）速度快。 2）简单易于理解，直接看到各个特征的权重。 3）能容易地更新模型吸收新的数据。	特征处理复杂。需要归一化和较多的特征工程。
SVM支持向量机	1）可以解决小样本下机器学习的问题。 2）提高泛化性能。 3）可以解决高维、非线性问题。超高维文本分类仍受欢迎。 4）避免神经网络结构选择和局部极小的问题。	1）对缺失数据敏感。 2）内存消耗大，难以解释。 3）运行和调参比较繁琐。

评估方法

不同的算法有不同的评价方法，正确而全面的评价方法能够很好的反应算法的性能，评价一个分类器算法的好坏又包括许多项指标，首先介绍一些基础概念。

常用术语

在分类的过程中，通常假设我们的分类目标只有两类，计为正例（positive）和负例（negative）分别是：

1. True positives(TP): 被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数；
2. False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
3. False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
4. True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。

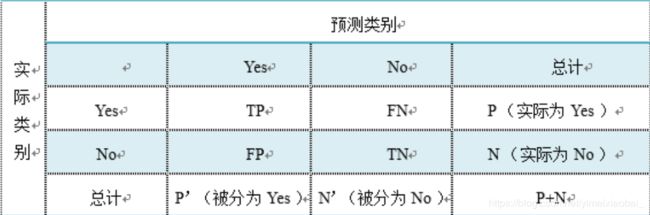
其中：
1）P=TP+FN表示实际为正例的样本个数。
2）True、False描述的是分类器是否判断正确。
3）Positive、Negative是分类器的分类结果，如果正例计为1、负例计为-1，即positive=1、negative=-1。用1表示True，-1表示False，那么实际的类标=TF*PN，TF为true或false，PN为positive或negative。
4）例如True positives(TP)的实际类标=1*1=1为正例，False positives(FP)的实际类标=(-1)*1=-1为负例，False negatives(FN)的实际类标=(-1)*(-1)=1为正例，True negatives(TN)的实际类标=1*(-1)=-1为负例。

在多实例中正例和负例也可以理解成目标类别与其他类的区别，我们在统计划分的过程中主要关注的还是目标类别。

评价指标

1. 正确率（accuracy）
   正确率是分类算法中最常见的评价指标，accuracy = (TP+TN)/(P+N)，正确率是被分对的样本数在所有样本数中的占比，通常来说，正确率越高，分类器越好。
2. 错误率（error rate)
   错误率则与正确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(P+N)，正确率 =1 - 错误率。
3. 灵敏度（sensitivity）
   sensitivity = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。
4. 特异性（specificity)
   specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。
5. 精度（precision）
   precision=TP/(TP+FP)，精度是精确性的度量，表示被分为正例的示例中实际为正例的比例。
6. 召回率（recall）
   召回率衡量正例被正确划分的比例，recall=TP/(TP+FN)=TP/P。与灵敏度是一样的。
7. 精度和召回率反映了分类器分类性能的两个方面。如果综合考虑查准率与查全率，可以得到新的评价指标F1-score，也称为综合分类率：$F1=\frac{2\times precision\times recall}{precision+recall}$。

对于分类算法还有其他的评价指标，如运行速度，鲁棒性，扩展性等。这些也是衡量算法性能的一部分。

回归算法

回归算法的目的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归算法通常输出的是实数值

常用算法

常见的回归算法按照因变量的不同可分为：多重线性回归，逻辑回归，泊松回归，负二项回归等。

评估方法

因为回归算法通常得到的结果是一个实数值，所以不是简单的对或者错，我们通常使用期望值来判断其性能的好坏。

常用术语

期望，方差，评价误差等统计学概念。

评价指标

方差（variance）：描述预测值P的变化范围、离散程度，是预测值的方差，也就是离期望值E的距离；方差越大，数据的分布也就越分散。这是最简单的评价预测值和期望值之间距离的方法。

MAE（absolute error loss） ：绝对误差损失的期望值。

MSE（mean squared Error）：均方误差，描述的真实值减去预测值，然后平方之后求和平均

RMSE（ROOT mean squarederror）：均方根误差，均方差开根号，实质上还是一样的。

交叉熵损失（cross-entropy loss）