几种凹凸贴图(Bump Mapping)的学习记录
凹凸贴图简介
凹凸贴图是纹理的一种应用,它主要用来实现类似砖块、墙体的那种凹凸不平的效果,相较于一般的纹理映射,它并不是通过纹理映射来改变材质本身的颜色,而是改变或扰动其法线的方向,而法线的方向被用在光线模型中,改变法线的方向就可以影响物体表面光照的明暗效果。因此,凹凸贴图实际上是一种欺骗式的手段,它并没有改变顶点的位置,让物体本身的模型变得凹凸不平,而是影响用户的视觉效果,让用户以为模型是凹凸不平的。凹凸贴图的实现只需要2个三角形,而不是用户误以为的复杂的模型。
凹凸贴图(Bump Mapping)的实现方法有多种,这里记录三种实现方法:法线贴图(Normal Mapping)、视差贴图(Parallax Mapping)、浮雕贴图(Relief Mapping)

切线空间
在法线贴图中,需要提供两张纹理——材质纹理和法线纹理,而在视差贴图和浮雕贴图中,还需要提供一张高度图纹理。法线纹理的作用是提供一个法线信息,纹理中对应的rgb的颜色值分别代表法线向量的分量,但是,这个向量是在什么空间下的向量?首先可以设想一下,这个向量如果是世界坐标系下的合不合理?很显然,在实际的渲染中,物体是有可能作变换的,如果一个物体进行了旋转变换,那么它的法线也要作相应的变换,法线纹理存的信息就不可以直接使用,要做相应的变换。似乎这种想法并不是最优的,但如果场景中有很多静态的物体也可以考虑使用。还有一种想法是存储在模型空间下的向量,这种想法似乎可行,并且比世界坐标系下的要好很多,但是这种方法太过于依赖模型本身的细节,如果模型发生了形变,这个向量依旧需要做变换,而且复用率不高,一个模型的法线纹理不好用在其他的模型上。
那么一种更好的方式,也是绝大多数凹凸贴图中的实现方式是让法线纹理存储在切线空间下的坐标,切线空间,肯定是跟切线有关的一个空间。对于一个顶点,它的法线方向是已知的,现在需要构造一个坐标系,让这个法线方向为Z轴,再选取两条过该点的切线,作为另外两个轴,其中一条称为Tangent,另一条称为Bit-Tangent,即切线空间的基为TBN,问题是,如何选这两条切线?与法线垂直的直线有无数条,构成了一个切平面,应该选取这个平面上哪两条互相垂直的直线?对于三角网络,可以想到利用纹理坐标(u,v)来构造,关于具体的构造方法我查阅的相关资料似乎都略有不同,具体探讨可见为什么要有切线空间(Tangent Space),它的作用是什么?。
使用切线空间的好处:
1.自由度高,独立于模型而存在,可以尝试用在不同的网格模型上
2.可以复用,例如一个正方体的六个面完全可以使用相同的切线坐标
3.纹理可压缩,切线空间下的Z坐标往往都是正值,因此可以在内存中只存储X、Y的坐标值,通过模长为1来计算Z的坐标值
事实上,无论采用哪种空间,只要最终能够让视线向量、光线向量、法线向量统一在一个线性空间下做与光照相关的运算就可以了,因此也没有必要拘泥于到底是哪个空间下好。但这并不意味着最终统一在哪个空间下不重要,注意这里所说的是法线信息存储在哪个空间下并不需要太钻牛角尖,而实际运算中,究竟是要将这三者统一在切线空间还是世界空间下,或者别的空间下是非常重要的。

法线贴图原理及实现
如前文所述,法线贴图的原理就是直接指定顶点在切线空间下的法线位置,用在材质纹理下的颜色信息和法线纹理下的法线信息来做光照的相关运算。实际编码最重要的一个环节就是将视线、法线、光线统一到一个空间下。有两种方式:一是将切线空间下的法线变换到世界空间下,然后直接利用世界空间下的光线、视线做运算,这种方法比较简明,但是性能略显不足,注意对于每一个像素的法线信息都是要靠插值求得的,也就是说,这样处理每个像素的法线都要做一次线性变换到世界空间下,它的计算是逐像素的;另一种方法是将世界空间下的视线、光线都变换到切线空间下,这种处理只需要逐顶点计算。
下面我们采用第一种方式来计算,比较好处理:
现在假设我们有了TBN的值,构造了如下矩阵 [ T x B x N x T y B y N y T z B z N z ] \begin{bmatrix} Tx & Bx & Nx \\ Ty & By & Ny \\ Tz & Bz & Nz \end{bmatrix} ⎣⎡TxTyTzBxByBzNxNyNz⎦⎤,这是从切线空间到世界空间的过渡矩阵,而由过渡矩阵和坐标变换的关系可知, [ T x B x N x T y B y N y T z B z N z ] ∗ [ X t Y t Z t ] = [ X w Y w Z w ] \begin{bmatrix} Tx & Bx & Nx \\ Ty & By & Ny \\ Tz & Bz & Nz \end{bmatrix} * \begin{bmatrix} Xt \\ Yt \\ Zt \end{bmatrix} = \begin{bmatrix} Xw \\ Yw \\ Zw \end{bmatrix} ⎣⎡TxTyTzBxByBzNxNyNz⎦⎤∗⎣⎡XtYtZt⎦⎤=⎣⎡XwYwZw⎦⎤ 如果我们把向量以行向量的形式表示,就可以得到 [ X t Y t Z t ] ∗ [ T x T y T z B x B y B z N x N y N z ] = [ X w Y w Z w ] \begin{bmatrix} Xt & Yt & Zt \end{bmatrix} * \begin{bmatrix} Tx & Ty & Tz \\ Bx & By & Bz \\ Nx & Ny & Nz \end{bmatrix} = \begin{bmatrix} Xw & Yw & Zw \end{bmatrix} [XtYtZt]∗⎣⎡TxBxNxTyByNyTzBzNz⎦⎤=[XwYwZw]
其中 [ X w Y w Z w ] \begin{bmatrix} Xw & Yw & Zw \end{bmatrix} [XwYwZw] 是世界空间下的法线方向, [ X t Y t Z t ] \begin{bmatrix} Xt & Yt & Zt \end{bmatrix} [XtYtZt]是切线空间下的法线方向。
这就是下面的UnityShader代码中的计算方式
Shader "custom/NormalMapping"
{
Properties
{
_MainTex("Main Texture",2D) = "white"{}
_NormalTex("Normal Texture", 2D) = "white"{}
_Specular("Specular", Range(1.0, 500.0)) = 250.0
_Gloss("Gloss", Range(0.0, 1.0)) = 0.2
}
SubShader
{
Tags{ "RenderType" = "Opaque" }
LOD 200
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
#include "AutoLight.cginc"
sampler2D _MainTex;
sampler2D _NormalTex;
float _Specular;
float _Gloss;
struct appdata
{
float2 uv : TEXCOORD0;
float4 vertex : POSITION;
float3 normal : NORMAL;
float4 tangent : TANGENT;
};
struct v2f
{
float4 pos : POSITION;
fixed2 uv : TEXCOORD0;
fixed3 light : TEXCOORD1;
fixed3 normal : TEXCOORD2;
fixed3 tangent : TEXCOORD3;
fixed3 bittangent : TEXCOORD4;
float4 worldPos : float;
LIGHTING_COORDS(5, 6)
};
v2f vert(appdata i)
{
v2f o;
o.uv = i.uv;
o.pos = UnityObjectToClipPos(i.vertex);
o.worldPos = mul(unity_ObjectToWorld, i.vertex); //顶点世界坐标
o.normal = normalize(UnityObjectToWorldNormal(i.normal)); //顶点的法线
o.tangent = normalize(mul(unity_ObjectToWorld,i.tangent).xyz); //顶点的切线
o.bittangent = normalize(cross(o.normal, o.tangent)); //顶点的副切线
o.light = WorldSpaceLightDir(i.vertex); //顶点的光线方向
return o;
}
fixed4 frag(v2f i) : COLOR
{
fixed4 texColor = tex2D(_MainTex,i.uv); //材质颜色
float3x3 tangentTransform = float3x3(i.tangent,i.bittangent,i.normal); //世界空间-切线空间 过渡矩阵
fixed3 norm = UnpackNormal(tex2D(_NormalTex,i.uv)); //切线空间下的法线
half3 worldNormal = normalize(mul(norm,tangentTransform)); //变换法线
//光照计算
fixed3 worldViewDir = normalize(UnityWorldSpaceViewDir(i.worldPos));
fixed3 ambi = UNITY_LIGHTMODEL_AMBIENT.xyz;
fixed3 diff = _LightColor0.rgb * saturate(dot(worldViewDir,worldNormal));
fixed3 lightRef = normalize(reflect(-i.light,worldNormal));
fixed atten = LIGHT_ATTENUATION(i);
fixed3 spec = _LightColor0.rgb * pow(saturate(dot(lightRef,worldViewDir)),_Specular)*_Gloss;
fixed4 fragColor;
fragColor.rgb = float3((ambi+(diff+spec)*atten)*texColor);
fragColor.a = 1.0f;
return fragColor;
}
ENDCG
}
}
FallBack "Diffuse"
}
个人对UnityShader的编写还不是很熟悉,所以肯定存在很多不足。法线贴图的效果见简介处图。下面的是法线贴图用到的两张纹理:


视差贴图原理及实现
法线贴图在一定程度上实现了视觉上的凹凸效果,但是还是存在着不足之处,当视线不与平面垂直,或者说与平面的法线偏离很大的角度时,凹凸效果逐渐变差。

现在考虑这样的一种情况:

红线描绘的轮廓代表设定的凹凸状态,即法线贴图中所蕴含的凹凸信息,下边的黑色直线代表我们使用的2个三角形代表的平面。现在人眼透过光线看平面上的点B,如果采用法线贴图的方式,会怎样处理?
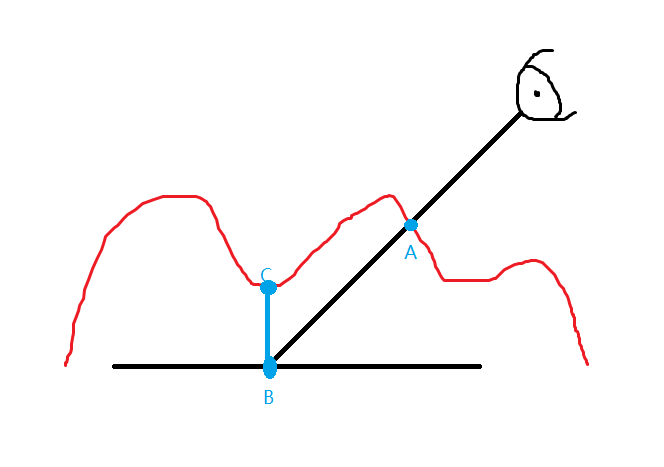
法线贴图会根据平面上B点的纹理坐标来对应相应的法线信息,也就是说最终的B点将表现为C点的效果——然而这并不是正常视觉效果下的结果。因为这个时候,人眼看到的应该是A点,而不是C点,当人眼与平面恰好垂直时,C点与A点重合,这是法线贴图最理想的情况,但是随着人眼与平面的法线成一定的角度,法线贴图近似的效果就越来越不符合真实的视觉感受,
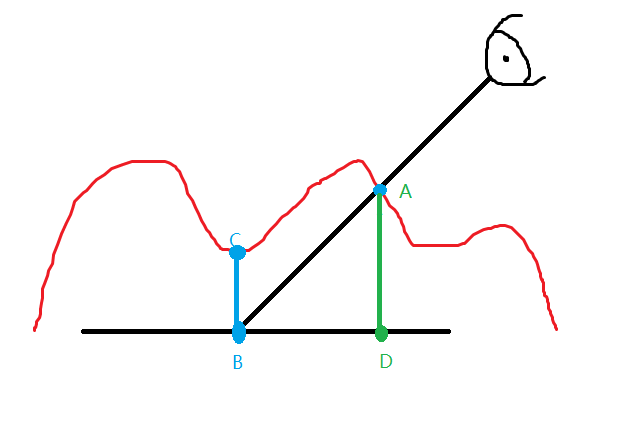
为了让B表现出A的效果,就不能用B的纹理坐标来采样法线信息了,应该使用A点对应的D点所代表的纹理坐标来获取法线信息,这就是视差贴图的核心思想。
现在的问题就是,如果将B点变换到D点?精确的计算显然很难实现,因此很有必要采用一种近似的方法。视差贴图的做法是,预备一张高度图,

注意这里的图是一张反色图,它其实是一张深度图。
前文所述切线空间下TB的选取是根据uv坐标的变换来选取的,因此很容易想到,由B到D的UV偏移应该就是朝着视线在切线空间下的方向。那么问题是应该偏移多少?这里是由经验或者说直觉来进行的一个粗略近似,即原位置越高的点需要偏移的越多,因此得出偏移的式子
p . u v = p . u v + v i e w D i r . x y ∗ h e i g h t ∗ f a c t o r p.uv = p.uv + viewDir.xy * height * factor p.uv=p.uv+viewDir.xy∗height∗factor
其中factor是一个系数,调整它来达到最好的效果。
还有一种方式是 p . u v = p . u v + v i e w D i r . x y ∗ h e i g h t ∗ f a c t o r / v i e w D i r . z p.uv = p.uv + viewDir.xy * height * factor / viewDir.z p.uv=p.uv+viewDir.xy∗height∗factor/viewDir.z
这里是为了更好地近似视线朝向顶部时的情况,当视线朝向顶部的时候所需要的偏移往往非常大。当然这一处理也可被省略。
// Upgrade NOTE: replaced '_Object2World' with 'unity_ObjectToWorld'
// Upgrade NOTE: replaced 'mul(UNITY_MATRIX_MVP,*)' with 'UnityObjectToClipPos(*)'
// Upgrade NOTE: replaced '_Object2World' with 'unity_ObjectToWorld'
Shader "custom/NormalMapping"
{
Properties
{
_MainTex("Main Texture",2D) = "white"{}
_NormalTex("Normal Texture", 2D) = "white"{}
_HeightTex("Height Texture", 2D) = "white"{}
_Specular("Specular", Range(1.0, 500.0)) = 250.0
_Gloss("Gloss", Range(0.0, 1.0)) = 0.2
_HeightFactor("Height" , Range(0.0,1.0)) = 0.2
}
SubShader
{
Tags{ "RenderType" = "Opaque" }
LOD 200
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
#include "AutoLight.cginc"
sampler2D _MainTex;
sampler2D _NormalTex;
sampler2D _HeightTex;
float _Specular;
float _Gloss;
float _HeightFactor;
struct appdata
{
float2 uv : TEXCOORD0;
float4 vertex : POSITION;
float3 normal : NORMAL;
float4 tangent : TANGENT;
};
struct v2f
{
float4 pos : POSITION;
fixed2 uv : TEXCOORD0;
fixed3 light : TEXCOORD1;
fixed3 normal : TEXCOORD2;
fixed3 tangent : TEXCOORD3;
fixed3 bittangent : TEXCOORD4;
fixed3 view : TEXCOORD5;
float4 worldPos : float;
LIGHTING_COORDS(5, 6)
};
v2f vert(appdata i)
{
v2f o;
o.uv = i.uv;
o.pos = UnityObjectToClipPos(i.vertex);
o.worldPos = mul(unity_ObjectToWorld, i.vertex); //顶点世界坐标
o.normal = normalize(UnityObjectToWorldNormal(i.normal)); //顶点的法线
o.tangent = normalize(mul(unity_ObjectToWorld,i.tangent).xyz); //顶点的切线
o.bittangent = normalize(cross(o.normal, o.tangent)); //顶点的副切线
float3x3 tangentTransform = float3x3(o.tangent, o.bittangent, o.normal); //世界空间-切线空间 过渡矩阵
o.light = mul(tangentTransform,WorldSpaceLightDir(i.vertex)); //切线空间 光线
o.view = mul(tangentTransform,UnityWorldSpaceViewDir(i.vertex));// 切线空间 视线
return o;
}
fixed4 frag(v2f i) : COLOR
{
fixed4 texColor = tex2D(_MainTex,i.uv); //材质颜色
float height = tex2D(_HeightTex, i.uv).r; //高度值
i.uv = i.uv + height * -i.view * _HeightFactor; //偏移
fixed3 norm = UnpackNormal(tex2D(_NormalTex,i.uv)); //切线空间下的法线
//光照计算
fixed3 ambi = UNITY_LIGHTMODEL_AMBIENT.xyz;
fixed3 diff = _LightColor0.rgb * saturate(dot(i.view,norm));
fixed3 lightRef = normalize(reflect(-i.light,norm));
fixed atten = LIGHT_ATTENUATION(i);
fixed3 spec = _LightColor0.rgb * pow(saturate(dot(lightRef,i.view)),_Specular)*_Gloss;
fixed4 fragColor;
fragColor.rgb = float3((ambi+(diff+spec)*atten)*texColor);
fragColor.a = 1.0f;
return fragColor;
}
ENDCG
}
}
FallBack "Diffuse"
}
这里将视线与光线都变换到了切线空间下。最终的效果为:

可以看到凹凸感有了明显的提示,但是也有很大的不足,当视线接近水平时,有了一定的扭曲,究其原因是在做UV偏移的时候偏移值不是精确的,是非常粗糙的一个值,那么针对此视差贴图有一些改进手段,其中一种就是浮雕贴图(Relief Mapping)
浮雕贴图原理及实现
浮雕贴图的原理简要的来说就是:在算偏移的时候进行一次光线追踪。当然光线追踪也没有那么复杂,本质上就是一种求交的手段。
这里以深度图代替高度图,

如图,每次都沿着视线方向步进一定的距离,当视线方向的深度低于目标位置纹理对应的深度时,继续步进,直到视线方向的深度高于目标位置纹理的深度。步进结束后,对最后两次的结果再作一次线性插值就可以得到最终的uv。
Shader "custom/NormalMapping"
{
Properties
{
_MainTex("Main Texture",2D) = "white"{}
_NormalTex("Normal Texture", 2D) = "white"{}
_HeightTex("Height Texture", 2D) = "white"{}
_Specular("Specular", Range(1.0, 500.0)) = 250.0
_Gloss("Gloss", Range(0.0, 1.0)) = 0.2
_HeightFactor("Height" , Range(0.0,1.0)) = 0.2
}
SubShader
{
Tags{ "RenderType" = "Opaque" }
LOD 200
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
#include "AutoLight.cginc"
sampler2D _MainTex;
sampler2D _NormalTex;
sampler2D _HeightTex;
float _Specular;
float _Gloss;
float _HeightFactor;
struct appdata
{
float2 uv : TEXCOORD0;
float4 vertex : POSITION;
float3 normal : NORMAL;
float4 tangent : TANGENT;
};
struct v2f
{
float4 pos : POSITION;
fixed2 uv : TEXCOORD0;
fixed3 light : TEXCOORD1;
fixed3 normal : TEXCOORD2;
fixed3 tangent : TEXCOORD3;
fixed3 bittangent : TEXCOORD4;
fixed3 view : TEXCOORD5;
float4 worldPos : float;
LIGHTING_COORDS(5, 6)
};
v2f vert(appdata i)
{
v2f o;
o.uv = i.uv;
o.pos = UnityObjectToClipPos(i.vertex);
o.worldPos = mul(unity_ObjectToWorld, i.vertex); //顶点世界坐标
o.normal = normalize(UnityObjectToWorldNormal(i.normal)); //顶点的法线
o.tangent = normalize(mul(unity_ObjectToWorld,i.tangent).xyz); //顶点的切线
o.bittangent = normalize(cross(o.normal, o.tangent)); //顶点的副切线
float3x3 tangentTransform = float3x3(o.tangent, o.bittangent, o.normal); //世界空间-切线空间 过渡矩阵
o.light = normalize(mul(tangentTransform,WorldSpaceLightDir(i.vertex))); //切线空间 光线
o.view = normalize(mul(tangentTransform,UnityWorldSpaceViewDir(i.vertex)));// 切线空间 视线
return o;
}
fixed4 frag(v2f i) : COLOR
{
int layer = 10;
float layerdepth = 1.0f / layer;
fixed4 texColor = tex2D(_MainTex,i.uv); //材质颜色
float depth = tex2D(_HeightTex, i.uv).r; //高度值
float currentDepth = 0;
int j= 0;
fixed2 deltauv = _HeightFactor * i.view / layer;
//步进
for ( ; j < layer ; j ++ )
{
i.uv -= deltauv; //偏移
depth = tex2D(_HeightTex, i.uv).r;
currentDepth += layerdepth;
if (currentDepth > depth)
{
break;
}
}
//线性插值
fixed2 prevUV = i.uv + deltauv;
float afterDepth = depth - currentDepth;
float beforeDepth = tex2D(_HeightTex,prevUV).r - currentDepth + layerdepth;
float weight = afterDepth / (afterDepth - beforeDepth);
i.uv = weight * prevUV + i.uv * (1.0 - weight);
fixed3 norm = UnpackNormal(tex2D(_NormalTex,i.uv)); //切线空间下的法线
//光照计算
fixed3 ambi = UNITY_LIGHTMODEL_AMBIENT.xyz;
fixed3 diff = _LightColor0.rgb * saturate(dot(i.view,norm));
fixed3 lightRef = normalize(reflect(-i.light,norm));
fixed atten = LIGHT_ATTENUATION(i);
fixed3 spec = _LightColor0.rgb * pow(saturate(dot(lightRef,i.view)),_Specular)*_Gloss;
fixed4 fragColor;
fragColor.rgb = float3((ambi + (diff + spec)*atten)*texColor);
fragColor.a = 1.0f;
return fragColor;
}
ENDCG
}
}
FallBack "Diffuse"
}
浮雕贴图最终的效果:

后两种方法的凹凸效果明显要比法线贴图好的多,而这三种方式也可看作是对前者的改进。
限于水平,有错误疏漏之处请指正