人工智能 一种现代方法 第6章 约束满足问题

定义约束满足问题

使用要素化来描述状态：一组变量，每个变量有自己的值。当每个变量都有自己的赋值同时满足所有关于变量的约束时，问题就得到了解决。这类问题就叫做约束满足问题（CSP），全称Constraint Satisfaction Problem。

CSP利用了状态结构的优势，使用的是通用策略而不是问题专业启发式来求解复杂问题。

主要思想：通过识别违反约束的变量/值的组合迅速消除大规模的搜索空间。

赋值：问题的状态由对部分或者全部变量的一个赋值来定义，{X_i=v_i,…}。
相容赋值、合法赋值：一个不违反约束条件的赋值。
完整赋值：每个变量都已经赋值。
部分赋值:只有部分变量赋值。
CSP的解是相容的、完整的赋值。

CSP包含三个成分X,D,C：

• X：变量集合 （variables）
• D：值域集合，每个变量有自己的值域 （domain）
• C：描述变量取值的约束集合 （constraint）

八皇后问题的CSP形式

• Variables: X={X1,X2,X3,…,X8}
• Domain: D={D1,D2,D3,…,D8},Di={1,2,3,4,5,6,7,8}
• Constraints:C={<{Xi,Xj}, Xi≠Xj & |Xi-Xj|≠|i-j|, 1 ≤ i ≤ 8,1 ≤ j ≤ 8}
  a solution {5,2,4,6,8,3,1,7}

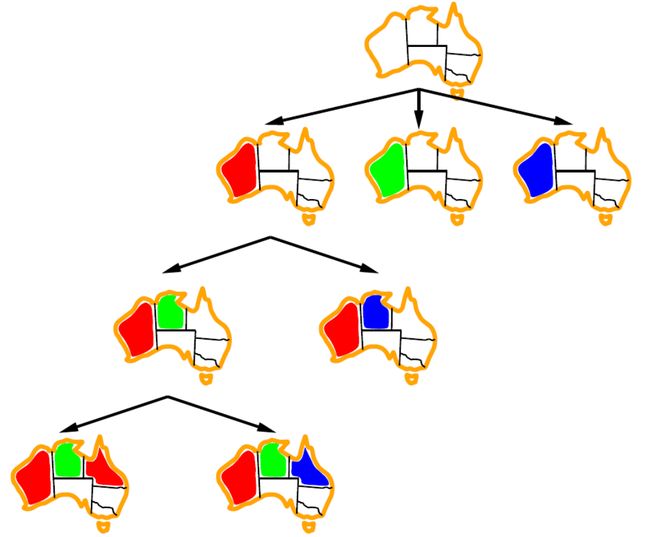
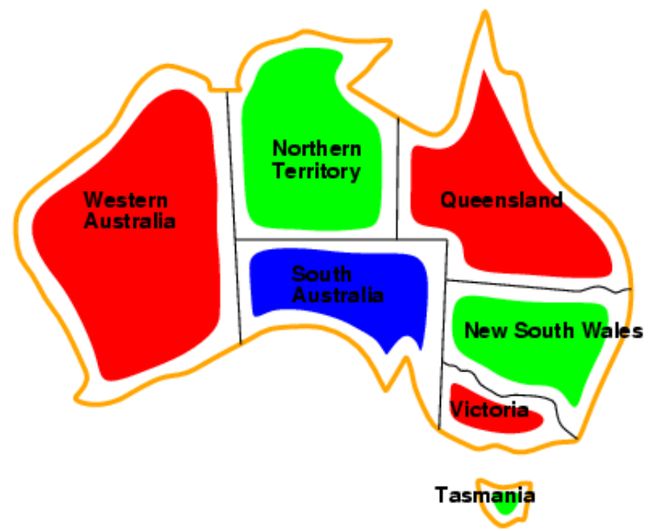
地图着色问题
任务：对澳大利亚地图的每个州进行着色，每个区域可以涂上红色、绿色或者蓝色，要求是相邻的区域颜色不能相同。
下图中的右图就是左图所示的罗马尼亚问题的约束图

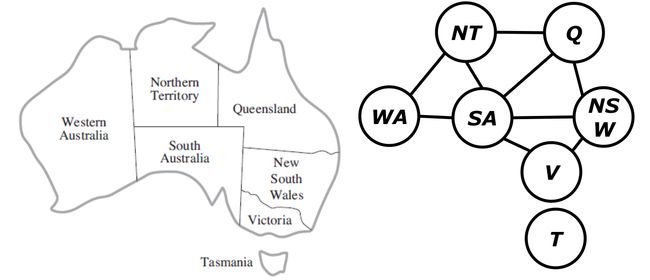
地图着色问题的CSP形式化

• Variables: X={WA, NT, Q, NSW, V, SA, T}
• Domain: D={D 1 ,…,D 7 }, D i ={red, green, blue}
• Constraints: adjacent regions must have different colors：C={WA≠NT, WA≠SA, NT≠SA, NT≠Q, SA≠Q,SA≠W, SA≠V,Q≠NSW, NSW≠V}
  SA≠WA是< (SA, WA),SA≠WA>的简洁表示

Solutions are assignments satisfying all constraints：
{WA=red, NT=green, Q=red,NSW=green, V= red, SA=blue,T= green}

约束传播：CSP中的推理

CSP中的推理:约束传播。约束传播使用约束减小一个变量的合法取值范围,从而影响到跟此变量有约束关系的另一变量的取值。
局部搜索(local search)：全部赋值full assignment
约束传播(constraint propagation)：部分赋值partial assignment

• 给一个变量赋值后,则通过约束传播可缩小与其有约束关系的其他变量的值域。

例如

• 在CSP中,算法可以进行约束传播,也可以搜索(从几种可能性中选择新的变量赋值)。约束传播与搜索可以交替进行,或者也可以将约束传播作为搜索前的预处理步骤。
• 约束传播的核心思想是局部相容性。
• 增强约束图中各部分局部相容性会导致不相容的结点取值被删除。

结点相容

如果单个变量(对应于CSP网络中的结点)值域中的所有取值满足它的一元约束,就称此变量是结点相容的。
例如,如果地图着色问题中南澳洲人不喜欢绿色,变量SA原来值域为{red, green, blue},删除green此结点即为结点相容的,此时SA的值域为{red, blue}。
如果网络中每个变量都是结点相容的,则此网络是结点相容的。

弧相容

对于变量Xi，Xj ,若对Xi的每个赋值在Xj都存在某个取值满足弧(Xi, Xj)的二元约束,则称Xi对于Xj是弧相容的。
如果每个变量对于其它变量都是弧相容的,则称该网络是弧相容的。

路径相容

对{Xi , Xj}的每一个相容赋值{Xi =a, Xj =b},Xm都有合适的取值同时使得{Xi , Xm }和{Xm , Xj }是相容的,则称集合{Xi , Xj }对于Xm 是(路径)相容的。被称为路径相容,是因为这很像是一条从Xi途经Xm，再到Xj的路径。

k-相容

如果对于任何k-1个变量的任何相容赋值,任何第k个变量总能被赋予一个和前k-个变量相容的值,那么这个CSP是k相容的。
1-相容是节点相容。2-相容即为弧相容。对二元约束网络,3-相容是路径相容。

全局约束

全局约束可涉及任意个约束变量(此处说的全局约束不一定是所有变量)。例如,Alldiff约束表示所有相关变量必须取不同的值。Alldiff约束的不相容检测的一种简单形式:如果约束涉及m个变量,可能的不同取值有n个,且m>n,那么约束不可能满足。

另一个重要的高阶约束是资源约束,有时称为atmost约束。例如在调度问题中,用P1 ,…,P4 表示执行四项任务的人数。总人数不超过10人的约束记为atmost(10, P1 , P2 , P3 , P4)。

CSP形式化为一个搜索问题(CSP的回溯搜索)

在CSP中,算法可以进行约束传播,也可以搜索(从几种可能性中选择新的变量赋值)。
很多CSP只用推理是无法求解的，还需要通过搜索来求解。
部分赋值的回溯搜索算法：可以用标准的深度优先搜索，状态可能是部分赋值，行动是将var=value加入到赋值中。
CSP的一个性质：变量赋值是可交换的，不用考虑变量赋值的顺序。

例子：澳大利亚地图着色的一个部分搜索树如下

回溯搜索，深度优先搜索的一种形式，经常用于求解CSP问题。每次为一个变量选一个赋值，没有合法的值的时候就回溯。推理和搜索可以交错进行（如前向检验、弧相容检验）。

如何提高回溯搜索的效率

变量顺序(最少剩余值、最大度)、值的顺序(最少约束值)、提前检查失败(前向检验、维护弧相容)、利用树形结构
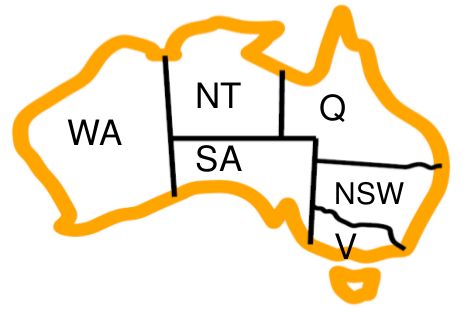
还是以澳大利亚地图着色为例：

变量顺序

1）选择“合法”取值最少或失败优先的变量——称为 最少剩余值（MRV） 启发式。（做一个强有力的引导，方便提早遇到失败，从而剪枝）

如果变量都有同样的最少剩余值，该怎么选呢？
2）度启发式：通过选择与其他未赋值变量约束最多的变量来试图降低未来的分支因子。（用来打破僵局，如选择第一个着色区域）

取值顺序

上面讲了怎么选取变量，一旦变量选好了，变量的值应该怎么选呢？
最少约束值：优先选择的赋值是给邻居变量留下更多的选择
下图中，右上角的Q应选择红色，若选择蓝色，则SA没有可选的颜色了

如何提前检查失败（搜索与推理交错进行）

前向检验(Forward Checking)：检查未分配变量的合法剩余值，当任何变量没有合法值时终止。

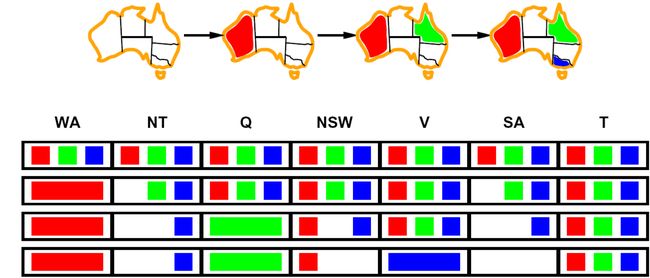
上图中，长条形颜色表示给对应地图上色，正方形颜色表示未上色，但是可以选择的颜色，按顺序对WA，Q，V赋值后，SA值域为空，故算法立刻回溯。

前向检验能检测出很多不相容，但是它无法检测所有不相容。它使当前变量弧相容，但是并不向前看使其他变量弧相容。上图中第三行，当WA，Q都赋值后，NT和SA都是能是蓝色了。前向检验向前看得不够远，不足以观察出这种不相容；NT和SA邻接所以不能取相同的值。

如何更早地比前向检验检查失败呢？

弧相容(Arc consistency)检验：当变量X赋值后，弧相容从与X相邻的弧中所有其他没有赋值的变量出发，若一旦某个变量的值域变为空，则算法立刻回溯。

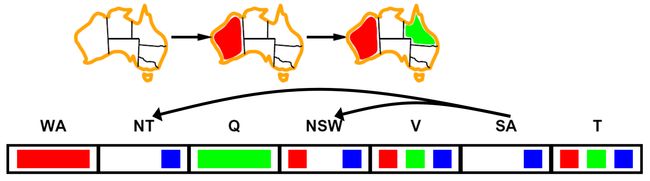
上图中，当WA，Q都赋值后，弧相容算法可以检测和SA邻接的NT的取值。若NT没有可取的值，则回溯。
弧相容检测故障早于前向检查

CSP局部搜索

局部搜索算法对求解许多CSP都是很有效的。它们使用完整状态的形式化：初始状态是给每个变量都赋一个值，搜索过程是一次改变一个变量的取值。

问题的结构

Theorem: if the constraint graph has no loops,the CSP can be solved in O(nd^2 ) time.
Compare to general CSPs, where worst-casetime is O(d^n)

求解树结构CSP时，首先任意选择一个变量为树的根，选择变量顺序，这样每个变量在树中出现在父节点之后。这样的排序称为拓扑排序。

资源分享

实验代码下载：
https://github.com/yyl424525/AI_Homework
人工智能-一种现代方法中文第三版pdf、课件、作业及解答、课后习题答案、实验代码和报告、历年考博题下载：https://download.csdn.net/download/yyl424525/11310392