误差error，偏置bias，方差variance的见解

更新日志：2020-3-10

谢谢@ProQianXiao的指正。偏差-方差的确是在测试集中进行的。

之前的误解是，偏差和方差的计算是同一个模型对不同样本的预测结果的偏差和方差；而实际上是不同模型对同一个样本的预测结果的偏差和方差。

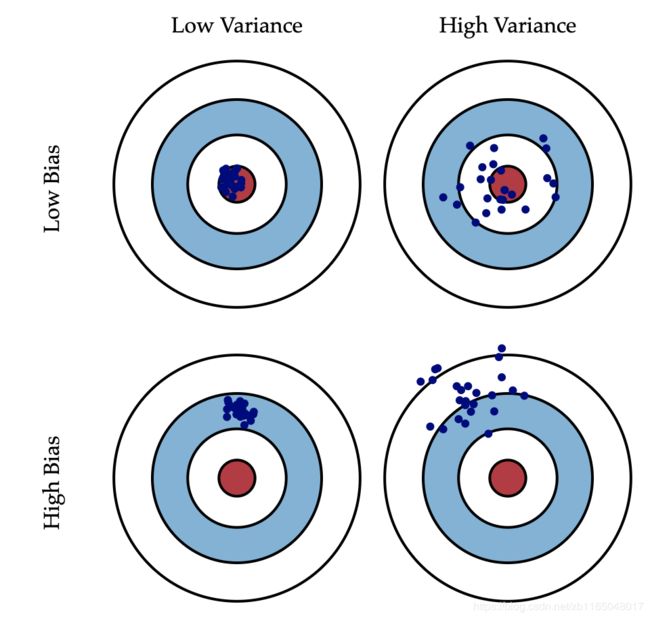
这时候就要祭出网上都有的这张图了

比如中间大红色点的是这个样本的真实标签，小小的蓝色点是不同样本的预测结果。接下来简介一下图：

1.最好的模型就是低偏差低方差，这样所有的模型觉得这个图片所属的标签相同，同时标签是真实标签

2.横排第二张图，所有的模型有不同的观点，导致预测结果方差很大，但是他们的预测结果都在真实标签附近徘徊，可能有点过拟合了

3.第二排的第一列，所有的模型都认为这个样本属于同一个标签，但是这个标签并不是真实标签，这就明显预测错误，有可能是模型刚初始化，所有权重都比较小且接近，也没训练，导致欠拟合。

4.第二排第二列，所有的模型都各抒己见，同时他们判断的结果与真实结果天差地别，这种情况我也不知道怎么称呼，不过训练久了一般不会出现这种情况吧。

综上，我们训练模型，通常会先出现方差小偏差大的情况，随后偏差慢慢减少，方差慢慢增大的情况，如果模型够好，也可能会出现偏差慢慢减少，方差慢慢减少的情况，这是最理想的结果。

——————————————————————————————————————————————

下面是之前的错误想法，是之前误解的偏差和方差是同一个模型在不同数据上的预测结果的偏差和方差。

不知怎么的，想到了这三个名词之间的关系，特地去查了一下，貌似学问还挺大。

以下纯属查阅资料，自己的理解，如有错误，谢谢下方评论纠正^_^

主要参考资料：知乎上关于这三个名词的讨论，以及周志华的《机器学习》这本书第45页，以及一篇英文文档。

偏置-方差是评估模型泛化能力的一个工具。

个人感觉这个评估是在训练的时候中进行的(训练过程用到了训练集和验证集)，因为大部分文献说 “bias是期望输出与真实标记的差，如果bias过小会产生过拟合” ；那么如果我们将这个“期望输出”理解为测试集的期望输出，得到 (测试集期望输出)-(实际标记) 的值，而我们的最终目标就是让这个值最小，怎么可能是这个值越小，过拟合会越严重呢？所以只有是 (训练集期望输出)-(实际标记) 的值非常小的时候，才会造成过拟合。也就是我们常说的 “在训练集上的误差很小，但是在测试集上的误差很大，那么得到的模型很可能是产生过拟合的模型”。

再举个栗子，在训练RBM的时候，能量函数或者计算神经元激活概率时都有一个偏置，这个偏置就只是在训练的时候不断更新，怎么可能是在测试的时候更新呢？这里有一个思路，是否可以通过偏置的大小或者平均值来判断RBM是否过拟合了呢~~~这个以后测试一下

说了这么多乱糟糟的，总结一下：

先说三个相关数据标记：①样本的真实标记 ②样本在训练集中的标记(可能含噪声)③样本在训练时每次得到的输出标记

噪声(noise)：训练集的标记与真实标记的误差平方的均值，即②-①的平方的均值。

偏置(bias)：训练模型的时候，每一次训练得到的训练集预测标签与原始真实标签的偏离程度(即③与①的差)，如果此偏离程度过小，则会导致过拟合的发生，因为可能将训练集中的噪声也学习了。所以说偏置刻画了学习算法本身的拟合能力，如果拟合能力不好，偏置较大，出现欠拟合；反之拟合能力过好，偏置较小，容易出现过拟合。在训练的时候可以发现这个bias理论上应该是逐渐变小的，表明我们的模型正在不断学习有用的东西。【当然这是针对只有一个训练集的情况下，如果有多个训练集，就计算出每一个样本在各个训练集下的预测值的均值，然后计算此均值与真实值的误差即为偏差】

方差(variance)：同样是针对训练模型时每一次得到的训练集预测标签，但是此时是最终一次训练以后得到的所有标签之间的方差且与真实标签无关(即③本身的方差)，即计算这些预测标签的均值，再计算(每一个标签-均值)的平方和。可以想象，刚开始方差肯定是很小的，因为刚开始学习，啥都不会，即使对于有或者无噪声的数据，我们都无法做出精准判断，然而随着学习的进行，有些我们会越学越好，但是会越来越多地受到噪声数据的干扰，方差也会越来越大。

误差(error)：预测标记与训练集中标记的误差(③和②的差)。

 

公式表示如下：

（以下样本均为训练集中的数据，与测试集毫无关系，且只训练了1个模型，用来测试的样本只是一类样本，比如拿一堆1来做分类；我当时有一个疑问就是我拿一个1和一个1000来分类，就算完全预测对，方差也很大。所以用来计算方差和均值的样本必须是同一类样本在模型的输出）

设样本真实标记为R，可能含噪声的训练集中的标记为T，最终训练得到的输出标记为P，符号E代表求平均。注意，R、T、P都是向量，表示有好几个样本。则

误差公式的证明详细请看周志华老师《机器学习》的P45

——————————————————————————————————————————————————————————————

整个理解过程主要碰到的疑问就是：

第一，bias的期望输出P到底来自测试集还是训练集。如果是测试集，怎么去解释bias越小过拟合。过拟合是测试集误差大。

第二，测试用的样本是原始标记是1和1000的时候，标签方差本身就很大，如何去理解这个方差小一点比较好。自己理解的是这个测试样本必须是同类样本，如果是1，那么所有拿来测试的必须全部是1，计算方差的时候，也就是计算标签为1的样本得到的实际输出的方差