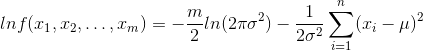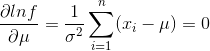多维高斯分布

 

我们常见的一维高斯分布公式为： 

 

                                                          

 

拓展到高维就变成：

 

                                                   

 

其中， 表示维度为  的向量，  则是这些向量的平均值，  表示所有向量  的协方差矩阵。 

本文简单探讨一下，上面这个 高维的公式是怎么来的。 

二维的情况

为了简单起见， 本文假设所有变量都是相互独立的。即对于概率分布函数  而言， 有  成立。 

现在，我们用一个二维的例子推出上面的公式。

假设有很多变量 , 他们的均值为 , 方差为 。

由于 ,  是相互独立的， 所以，  的高斯分布函数可以表示为: 

 

                                               

 

接下来，为了推出文章前边的高维公式我们要想办法得到协方差矩阵 

对于二维向量 而言， 其协方差矩阵为： 

                                                                                 

由于  是相互独立的， 所以  。 这样，   退化成   。

则  的行列式  ,  带入上边  的高斯分布函数  最后化简结果中（简称公式（4））就可以得到:

 

                                                

 

 这样一来，我们已经推出了公式的左半部分，下面， 开始处理右面的  函数。 

 原始的高维高斯函数的  函数为：  , 根据前面计算出来的  ， 我们可以求出它的逆：

 。

接下来根据这个二维的例子，将原始的  展开：

 

                                 

 

展开到最后，发现推出了公式（4）。说明原公式 是成立的。 你也可以将上面的过程逆着推回去，一样可以从例子中的公式（4）推出多维高斯公式。 

函数图像

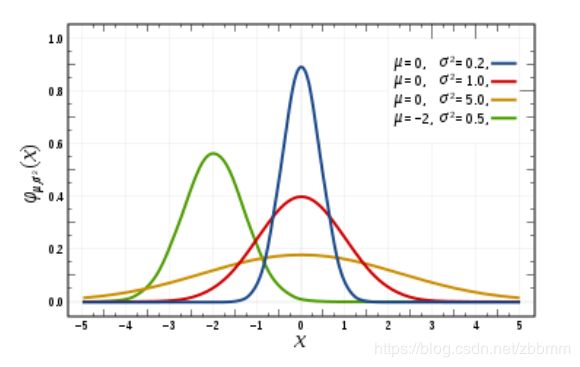
知道多维的公式后， 下面再简单比较一下一维和二维的图像区别。 

                                                  

上面展示的是4个一维高斯函数的图像。高斯函数是一个对称的山峰状，山峰的中心是均值  ，山峰的 [胖 瘦] 由标准差决定，如果 越大，证明数据分布越广，那么山峰越 [矮 胖] ， 反之， 则数据分布比较集中， 因此很大比例的数据集中在均值附近，山峰越[瘦 高] 。在偏离均值  三个  的范围外，数据出现的概率几乎接近0， 因此这一部分的函数图像几乎与  轴重合。

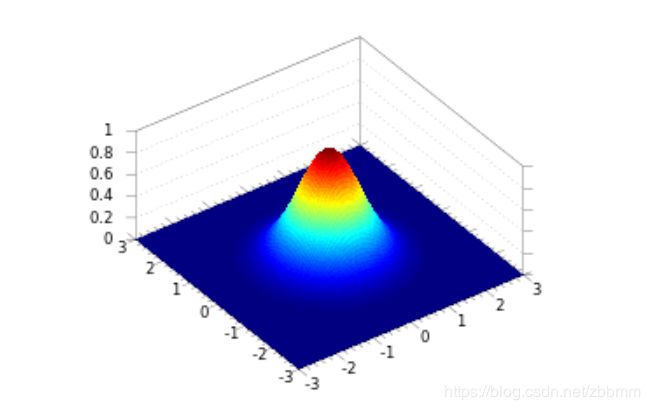
下面看二维的例子： 

 

                                             

有了一维图像的例子，二维图像就可以类比出来了。如果说，一维只是山峰的一个横截面，那么二维则是一个完整的有立体感的山峰。山峰的 [中 心] 和 [胖 瘦] 的一维的情况是一致的，而且， 对于偏离中心较远的位置，数据出现的概率几乎为0， 因此，函数图像在这些地方就逐渐退化成 [平 原] 了。 

参数估计 

另外，如果给定了很多数据点，并且知道它们服从某个高斯分布，我们要如何求出高斯分布的参数（ 和 ）呢？

当然，估计模型参数的方法有很多，最常用的就是极大似然估计。

简单起见，拿一维的高斯模型举例。假设我们有很多数据点： 。一维高斯函数是：

首先，我们先写出似然函数：

 

                                                

然后取对数：

 

                                              

 

求出导数，令导数为 0 得到似然方程：

 

                                                                              

 

                                                                          

 

我们可以求出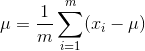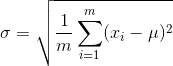： ,  ，可以看到，这其实就是高斯函数中平均值和标准差的定义。

对于高维的情况，平均值和协方差矩阵也可以用类似的方法计算出来。

总结

本文只是从一个简单的二维例子出发，来说明多维高斯公式的来源。在 PRML 的书中，推导的过程更加全面，也复杂了许多，想深入学习多维高斯模型的还是参考教材为准。

重新对比一维和多维的公式：

 

                                                               

 

                                                     

 

其实二者是等价的。一维中，我们针对的是一个数，多维时，则是针对一个个向量求分布。如果向量退化成一维，则多维公式中的  ,  ,  , 这时多维公式就退化成一维的公式。所以，在多维的公式中，我们可以把  当作是样本向量的标准差。

 

参考：

jermmyxu 关于多维高斯分布

Anomaly Detection | Multivariate Gaussian Distribution — [ Andrew Ng ]