成本函数/代价函数、损失函数、目标函数
 日萌社
日萌社
人工智能AI:Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战(不定时更新)
目标函数:既可代指损失函数,又可代指代价函数/成本函数。有的地方将损失函数和代价函数没有细分也就是两者等同的。
损失函数(Loss function):
损失函数越小,就代表模型拟合的越好。
例如有平方误差损失函数、二分对数损失函数(二元标签预测)、多分类对数损失(多分类标签预测)
代价函数/成本函数(Cost function):代价函数和成本函数意思一样。1.代价函数/损失函数
1.目的:如何把最有可能的直线与数据集中的数据相拟合
2.在线性回归的例子中有下面有一个训练集
h代表假设函数,即是用来预测的线性回归: 3.选择不同模型参数θ0和θ1,将会得到不同的(线性回归)假设函数 h(x)=θ0+θ1*x
1.图一:θ0=1.5。θ1=0。假设函数h则为 h(x)=1.5+0*x。这样是一个常数函数,恒等于1.5。
2.图二:θ0=0。θ1=0.5。假设函数h则为 h(x)=0+0.5*x。这是会穿过点(2,1),h(2)=0+0.5*2 结果值为 1。
3.图三:θ0=1。θ1=0.5。假设函数h则为 h(x)=1+0.5*x。这是会穿过点(2,2),h(2)=1+0.5*2 结果值为 2。 4.在线性回归的例子中有下面有一个训练集 1.目的:根据数据集 求出模型参数θ0和θ1的值,从而来让 (线性回归)假设函数 h(x)=θ0+θ1*x 表示出一条直线尽量地与数据点更好地拟合。
2.思考:当我们对 h(x)函数 输入 x(输入变量/输入特征值)时,要如何能使预测的值最接近样本的对应的y值,来从而求得模型参数θ0和θ1的值。
3.设计:在线性回归中,我们要解决的是一个最小化的问题,所以我们要写出模型参数θ0和θ1 的最小化的值,而且希望这个公式极其小,
想要h(x)和y之间的差异要小。
4.实现:
1.符号使用:
(x^(i),y^(i)) 代表第i个样本,即指第i行的样本。
x^(i) 指第i个样本中的 输入变量/输入特征值。y^(i)指第i个样本中的 输出变量/要预测的目标变量。
x^(1) 指第1个样本中的 房子的面积大小。y^(1) 指第1个样本中的 房子真实价格。
2.MSE(均方误差/平均误差)代价函数/成本函数: 平均误差代价函数的目的:
计算出 每个样本的预测值h(x^(i)) 减去 其实际值y^(i)的差的平方 便可求得每个样本的平均误差,
然后把每个样本的平均误差加起来的总和便是平均误差代价函数要求得的结果。
例如训练集中有样本(x^(i),y^(i))为(1,1)和(2,2),那么计算过程即为:
(1,1):h(1)得出的预测值 减去 实际值1 的差的平方
(2,2):h(2)得出的预测值 减去 实际值2 的差的平方
然后这两个样本所求得的平均误差相加的总和便是平均误差代价函数要求得的结果。
解析:1.m 指的是 训练集中的样本数量
2.(hθ(x^(i)) - y^(i))^2 可以简化写成 (h(x^(i)) - y^(i))^2
表示 预测值h(x^(i)) 减去 真实值y^(i) 之差的平方,即为预测值和真实值之间的平均误差/均方误差。
3.hθ(x^(i)) 可以简化写成 h(x^(i)),该公式实际为线性回归,原始公式的简化写法为 h(x)=θ0+θ1*x
当想要知道某个房子能卖出多少钱时,我们把这个房子大小用x^(i)来表示,然后作为h(x)函数的输入变量,
即得到 h(x^(i))=θ0+θ1*x^(i) 便可得出预测值(预测卖价),然后用该预测值h(x^(i))减去真实值y^(i)所得的差的平方
4.MSE(均方误差/平均误差)表示的是关于θ0和θ1的最小化过程,这意味着需要找到θ0和θ1的值来使平均误差表达式所求出的平均误差更小。
简单地说,找到能使训练集中“预测值和真实值的差的平方的和的”1/2m最小 的θ0值和θ1值。这是线性回归的整体目标函数。
5.上述 MSE(均方误差/平均误差)公式 可简化为 J(θ0,θ1),同样表示对函数J(θ0,θ1)求最小值。 6.之所以要求出误差的平方和,是因为误差平方代价函数对于回归问题是一个合理的选择,还有其他代价函数也能发挥很好的作用,
但平方误差代价函数可能是解决回归问题的最常用手段了。
3.(h(x^(i))-y^(i))^2:要求尽量减少假设的输出(预测值)与房子真实价格之间的差的平方。
4.要做的是对所有训练样本进行一个求和,即对 i=1 到 i=M 的所有训练样本进行一个求和,将对假设进行预测得到的结果。
5.h(x^(i)):此时输入第i号房子的面积大小,把所求出的第i号对应的预测结果 减去 第i号房子的实际价格 所得的差的平方 进行相加得到总和。
6.这个公式平均了所有预测错误,并且如果 预测值h(x^(i)) 远离 真实值(房子真实价格),那么两者之间的差的平方运算只会让差距更加明显。
因此希望尽量减少这个值,这个值指的是预测值和实际值的差的平方误差和,或者说 预测价格 和 实际卖出价格 的差的平方。
7.公式中的 m 均指的是 训练集中的样本容量数,比如 1/2m。尽量减少平均误差,因此对这个求和值的二分之一求最小值。
8.假设函数的简化写法为 h(x)=θ0+θ1*x
当x传入x^(i)得出公式:h(x^(i))=θ0+θ1*x^(i) 得出预测值。
2.MSE(均方误差/平均误差) 代价函数/成本函数 如下:
1.简化假设函数:hθ(x)=θ0+θ1*x
使假设函数仅包含参数θ1*x,可以把参数θ0视为0。
2.简化假设函数之后,平均误差代价函数中的表达式 hθ(x^(i)) 也变为 hθ(x^(i))=θ1 * x^(i)。
3.最终J(θ0,θ1) 也被简化为 J(θ1),优化目标便是尽量减少 J(θ1)的值。
4.用图表示就是:如果θ0=0时,相当于只选择了经过原点(0,0)的假设函数,使用简化的代价函数可以更好地理解3.假设函数 hθ(x)
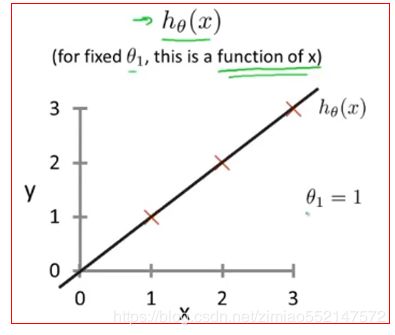
1.对于给定的θ1,这是一个关于x的函数,比如说关于房子尺寸x的函数。它控制着直线的斜率。
2.例子:当θ1=1时,假设函数 hθ(x)便可以表示为这条直线,横纵是房子大小x,纵轴便是房价y。4.代价函数 J(θ1)
此处讲解代价函数 J(θ0,θ1)时,把θ0看做0,即J(θ1)相当于只选择了经过原点(0,0)的假设函数,使用简化的代价函数可以更好地理解。
1.这是一个关于模型参数θ1的函数,横轴代表θ1,纵轴代表J(θ1)。它控制着直线的斜率。计算的是训练集中各项差值的平方的总和。
2.当代价函数简化为 hθ(x)=θ1*x 时,J(θ1)公式中的 hθ(x^(i)) 便可以简化为θ1*x^(i)。
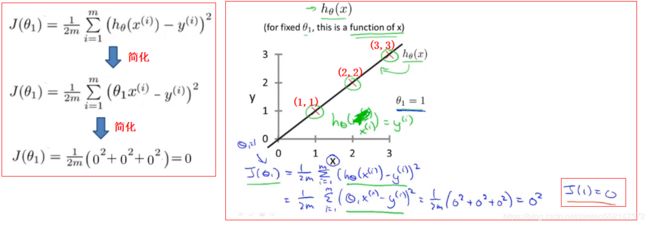
根据下图特殊的训练集得知,θ1*x^(i) 和 y^(i) 都为0,因为图中直线经过点(1,1),(2,2),(3,3),如果θ1=1,那么 h(x^(i)) 即 θ1*x^(i) 等于 y^(i),
结论为所有的 h(x)-y 都等于 0,便可以的得出 J(θ1)=1/2m(0^2+0^2+0^2)=0。
比如 J(1)=0。 3.例子1:代价函数J(1)的画图位置
结论:横轴代表θ1,纵轴代表J(θ1),当θ1=1时,那么J(1)结果值为0,则J(1)位于(1,0)的位置上。
解析:在代价函数J(θ1)中,假如θ1=1时,则J(θ1)=0。在下图中画出J(1)=0,实际在横轴上的值为1位置上画上红叉表示。 4.例子2:代价函数J(0.5)的画图位置
结论:横轴代表θ1,纵轴代表J(θ1),当θ1=0.5时,那么J(0.5)的点即位于(0.5,0.58)的位置上。
解析:
1.θ1 还可以取不同值,比如θ1 可以取 负数、整数、0。
2.在假设函数 hθ(x)中,假如θ1=0.5时,是一条斜率为0.5的直线,那么下面需要计算出代价函数J(0.5)的值。
下面计算3个样本,因此 m=3 的样本量
假设函数hθ(x)图中的 蓝色线的垂直长度 实际为 实际值y^(i) 与 预测值h(x^(i)) 的差值。
当θ1=0.5时,h(x^(i))=0.5*x^(i),即0.5乘以横轴上的x值得出预测值。
第一个样本:(0.5-1)^2。预测值为 0.5*1=0.5,实际值为 1。
第二个样本:(1-2)^2。预测值为 0.5*2=1,实际值为 2。
第三个样本:(1.5-3)^2。预测值为 0.5*3=1.5,实际值为 3。
计算流程:
J(0.5) = 1/2m * [(0.5-1)^2+(1-2)^2+(1.5-3)^2]
= 1/(2*3) * (0.25+1+2.25)
= 1/(2*3) * (3.5)
= 3.5/6 约等于 0.58
最终J(0.5)在代价函数图中的红叉位置
5.例子3:代价函数J(0)的画图位置
结论:横轴代表θ1,纵轴代表J(θ1),θ1=0即完全不在横轴上,那么J(0)的点完全位于纵轴上(0,2.3)的位置。
解析:
1.在代价函数J(θ1)中,假如θ1=0时,那么假设函数h(x)便为一条位于横轴上的水平线(红色线),那么每个样本的预测值h(x^(i))都为0.
2.下面计算3个样本,因此 m=3 的样本量
假设函数hθ(x)图中的 蓝色线的垂直长度 实际为 实际值y^(i) 与 预测值h(x^(i)) 的差值。
J(0) = 1/2m * [(0-1)^2+(0-2)^2+(0-3)^2]
= 1/(2*3) * (1^2+2^2+3^2)
= 1/6 * 14 约等于 2.3
最终 J(0)在代价函数图中的红叉位置
6.例子3:代价函数J(负数)的画图位置
结论:横轴代表θ1,纵轴代表J(θ1),当θ1=-0.5时,那么J(-0.5)的点完全位于纵轴上(-0.5,5.25)的位置。
解析:在代价函数J(θ1)中,假如θ1=-0.5时,那么假设函数h(x)=-0.5*x,即为斜率为-0.5的直线,此时产生的误差会非常大,
此时的代价函数求得的结果值约等于5.25。 7.结论:
此处讲解代价函数 J(θ0,θ1)时,把θ0看做0,即J(θ1)相当于只选择了经过原点(0,0)的假设函数,使用简化的代价函数可以更好地理解。
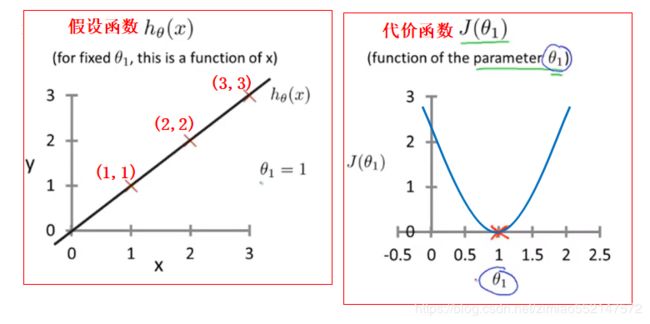
1.在代价函数J(θ1)中,随着θ1的变化,便可以把代价函数的结果值对应到图上画成点,那么代价函数J(θ1)如下图可以画出这个形状。 2.每个θ1值都对应一个不同的假设函数h(x),并且都可以得到一个不同的J(θ1)值。
3.学习算法的优化目标:
通过选择θ1的值获得最小的代价函数J(θ1)的值,这就是线性回归的目标函数。
比如当θ1=1时,那么J(1)结果值为0,在代价函数的曲线中位于最低位的(1,0),意味着这是最小的代价函数J(θ1)的值。
同时在假设函数中也产生一条最符合该样本数据的直线,这就是为什么要最小化J(θ1)来找到一条最符合该样本数据的直线。 4.横轴代表θ1,纵轴代表J(θ1)
1.当θ1=1时,那么J(1)结果值为0,则J(1)位于(1,0)。
假设函数hθ(x):红色线。代价函数J(θ1):红色叉。
2.当θ1=0.5时,那么J(0.5)结果值为0.58,则J(0.5)位于(0.5,0.58)。
假设函数hθ(x):蓝色线。代价函数J(θ1):蓝色叉。
3.当θ1=0时,则J(0)的点完全位于纵轴上(0,2.3)的位置。
假设函数hθ(x):绿色线。代价函数J(θ1):绿色叉。5.代价函数 J(θ0,θ1)
此处讲解代价函数 J(θ0,θ1)时,保留θ0和θ1,不再是前面讲解的省略θ0的 J(θ1)。
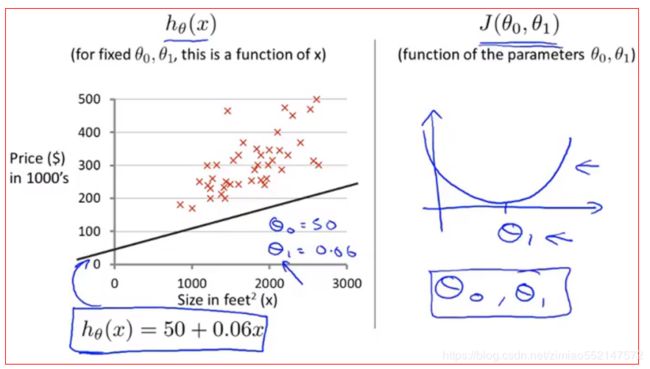
1.下面是关于住房的数据集,假设θ0=50,θ1=0.06,便得到假设函数h(x)=50+0.06以及得到左图(假设函数)中对应的直线,然后绘制右图(代价函数)中的碗形状的函数曲线。
不论是只保留保留的J(θ1) 还是 J(θ0,θ1),图形都是碗形状的函数曲线。 2.但是J(θ0,θ1)实际是如下图般的一个3D曲面图,该碗形状的3D曲面图实际就是J(θ0,θ1)代价函数的形状。
总是这样一个弓状的函数图,术语叫做凸函数,不太正规地解释凸函数就是一个弓形函数。
这个弓形函数不存在局部最优解/局部最低处,只存在一个全局最优解/全局最低处。
当计算这种弓形的代价函数的梯度下降时,只要你是使用线性回归,那么它总是会收敛到全局最优,因为没有其他的局部最优解/局部最低处。
J(θ0,θ1)的3D曲面图中:
横轴(水平坐标轴)轴标:为θ0和θ1。当改变θ0和θ1这两个模型参数时,将会得到不同的代价函数 J(θ0,θ1)的值 (θ0,θ1)点。
竖轴(垂直坐标轴)轴标:为J(θ0,θ1)的值。上下箭头红色线表示曲面的高度。
2.下面的讲解J(θ0,θ1)时,不使用3D曲面图展示曲面,而是换为使用等高线图(等高图像)来展示曲面。
右侧图中的等高线图(等高图像)表示J(θ0,θ1)代价函数。
1.轴为θ0和θ1,每一个椭圆形同为一个系列的J(θ0,θ1)值相同的点,比如说第二外层上的三个红色叉所在的点实际都均具有相同的J(θ0,θ1)值。
2.J(θ0,θ1)它的最小值实际位于3D曲面图的最底部的这一点,或者说是等高线图的同心椭圆的中心点。
3.在等高线图中,只要是在同一个椭圆形上,无论这个点是在同一个椭圆形上哪个位置,均都具有相同的曲面高度。 3.例子1:
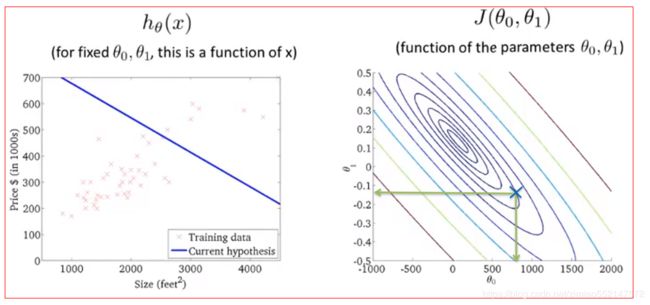
1.(右图)等高线图中的蓝色叉位置上的点:
这个(θ0,θ1)的值:θ0大概等于800,θ1大概等于-0.15。θ1为斜率。
这个(θ0,θ1)的值对应左图假设函数中的蓝色的函数直线,但是该蓝色的函数直线并没有很好地拟合数据。
因此得出结论:这个(θ0,θ1)的值(蓝色叉位置上的点)离最小值相当远。
2.(左图)假设函数:蓝色的函数直线并没有很好地拟合数据。 4.例子2:
1.(右图)等高线图中的红色叉位置上的点:
这个(θ0,θ1)的值:θ0大约等于360,θ1等于0。这个J(θ0,θ1)对应(左图)假设函数中的蓝色的水平线h(x)=360+0*x。
这个(θ0,θ1)的值所对应到(左图)假设函数中的蓝色的函数直线,也并没有很好地拟合数据,但至少比例子一的函数直线略好一点。
2.(左图)假设函数:
蓝色的函数水平线为 h(x)=360+0*x。
但是同样的这条函数水平线也并没有很好地拟合数据,但至少比例子一的函数直线略好一点。 5.例子3:
1.(右图)等高线图中的红色叉位置上的点:
这个(θ0,θ1)的值所对应到(左图)假设函数中的蓝色的函数直线,也并没有很好地拟合数据。
2.(左图)假设函数:
同样的这条函数水平线也并没有很好地拟合数据。 6.例子4:
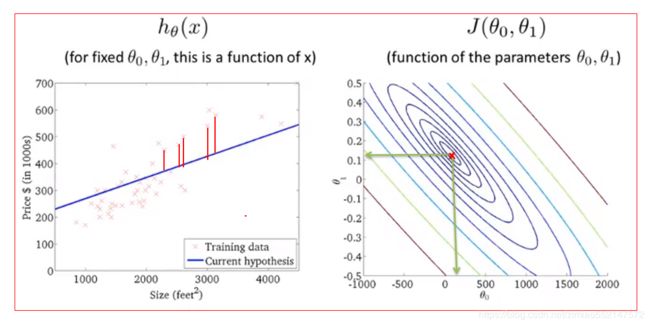
1.(右图)等高线图中的红色叉位置上的点:
这个(θ0,θ1)的值还不是最小值,但已经相当接近最小值了。
这个(θ0,θ1)的值对应到(左图)假设函数中的蓝色的函数直线,假设函数直线对数据拟合得还不错。
2.(左图)假设函数:
假设函数直线对数据拟合得还不错,但还不是拟合得最好的位置。
3.注意:
(左图)假设函数中,每个训练样本(粉红色叉所在点)到假设函数(蓝色)直线的距离(红色直线),
即 每个训练样本与预测值之间的距离的平方和,实质为 误差值。虽然依旧不是最小值,但是相当接近最小值。 7.结论
1.代价函数J(θ0,θ1)越接近最小值的点 意味着 对应更好的代价函数直线。
2.学习算法的意义:自动寻找代价函数的最小值对应的θ0和θ1。