关于单应性矩阵的理解：Homography matrix for dummies

尽量写的通俗一点，因为从某种程度上讲，本人也是dummy.....
1. 先说homogeneous coordinate，齐次坐标
一幅2D图像上的非齐次坐标为(x,y)，而齐次坐标为(x,y,1)，也可以写成(x/z,y/z,1)或(x,y,z)。齐次坐标有很多好处，比如可以很清楚的确定一个点在不在直线上：
T(x)*I=0,这里T表示转置；

还可以描述无穷远点：(x,y,0)；

还可以把平移和旋转写到一个矩阵里（也有不愿意这么干的，摄影测量里用的都是非齐次坐标，平移和旋转分开写）；

具体的可去看<计算机视觉中的多视图几何>,i.e.,。

2. Homography matrix，单应性矩阵
两个不同视角的图像上的点对的homogeneous coordinate可以用一个射影变换（projective transformation）表述，即：

x1 =H*x2

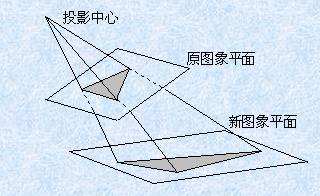
二维和三维的图示如下：

射影变换也叫“单应”--Homography，“Homo”前缀就是same的意思，表示“同”（homosexual大家都知道），homography就是用同一个源产生的graphy，中文译过来大概就是"单应"。

因此上面式子中的矩阵H就叫单应性矩阵。上式中的x1和x2都是3*1的齐次坐标，因此H是一个3*3的矩阵：{h00,h01,h02;h10,h11,h12;h20,h21,h22}。

然而，单应矩阵的自由度是多少呢？（参考https://www.zhihu.com/question/23310855）
如果给定一个单应H={h_ij}，给它的元素乘上同一个数a，得到的的单应a*H和H作用相同，因为新单应无非把齐次点x1变成了齐次点a*x1，都是一回事。因此我们可以把a换成1/h22，那么H就变成了只有8个自由元素的矩阵。
那么需要多少个点对求解这个H呢？如果需要唯一解的话，需要4个点对（对应8个方程，去解H中的8个未知数）。
关于这个话题的理解，可以继续参考：
http://blog.csdn.net/qq_19764963/article/details/52038748
http://cseweb.ucsd.edu/classes/wi07/cse252a/homography_estimation/homography_estimation.pdf
3. 举两个应用的例子。
例子1：两个图像的拼接
通过图像特征点匹配+RANSAC可以获得图像之间的单应性矩阵，然后把其中一个图像通过这个矩阵投影到另一个图像上就完成了基本的拼接。
例子2：在相机的内参数标定过程中会用到求解单应性矩阵
对一个棋盘格拍照，棋盘格的世界坐标系是用户任意设定的，标定的时候，默认世界坐标系就是以标定板左上角点为原点，z轴垂直于标定板，xoy面与标定板重合的三维直角坐标系。棋盘格的格子长度已知，因此可以知道各个角点的世界坐标系坐标XYZ（Z=0）。由于Z=0，因此可以忽略掉Z这个维度，世界坐标系中某个坐标(X,Y,Z,1)到图像坐标(x,y,1)的变换就等价于(X,Y,1)到图像坐标(x,y,1)的变换。此时的变换矩阵就由3*4变为3*3，成为了单应性矩阵。
因此用4个角点就可以计算H的8个参数。以不同的角度对棋盘格拍摄3张就可以得到3个H，如果用张正友标定法，就可以得到6个约束方程，可以求解B矩阵（对称矩阵）的6个未知参数，进而通过Cholesky分解求解出内参矩阵A的参数。