Bei_xifen
Bei_xifen

传输线方程与终端加载的无损耗传输线

目录

传输线方程

电压波和电流波

特性阻抗

无损耗传输线模型

终端加载的无损耗传输线

电压反射系数

传播常数与相速度

驻波与电压驻波比

传输线方程

将基尔霍夫电压、电流定律(KVL,KCL)应用于传输线微元的节点a

传输线方程与终端加载的无损耗传输线_第1张图片 传输线微元的电压回路和电流节点

这里需要说明一下，R、L、G和C表示的是单位长度传输线的量值，它们的单位是\Omega/m、H/m、S/m和F/m。

采用负数表示，由基尔霍夫电压定律可得

                                                              (R+j \omega L) I(z) \Delta z+V(z+\Delta z)=V(z)

将该式转化为微分方程，将微分传输线段两端的电压降组合成微商的形式

                                             \lim _{\Delta z \rightarrow 0}\left(-\frac{V(z+\Delta z)-V(z)}{\Delta z}\right)=-\frac{d V(z)}{d z}=(R+j \omega L) I(z)

即

                                                                            -\frac{d V(z)}{d z}=(R+j \omega L) I(z)                 (1)

对节点a应用基尔霍夫电流定律可得

                                                           I(z)-V(z+\Delta z)(G+j \omega C) \Delta z=I(z+\Delta z)

微分方程形式

                                                     \lim _{\Delta z \rightarrow 0} \frac{I(z+\Delta z)-I(z)}{\Delta z}=\frac{d I(z)}{d z}=-(G+j \omega C) V(z)                (2)

传输线方程

                                                                    \left\{\begin{array}{l}{\frac{\mathrm{d} \mathrm{V(z)}}{d z}=-(R+j \omega L) I(z)} \\ {\frac{\mathrm{dI(z)}}{d z}=-(G+j \omega C) V(z)}\end{array}\right.

电压波和电流波

传输线方程(1)式对空间求导得

                                                                      \frac{d^2 V(z)}{d z^2}=-(R+j \omega L) \frac{I(z)}{dz}

将传输线(2)式带入上式得

                                                                          \frac{d^2 V(z)}{d z^2}-\gamma^2 V(z)=0

同理可得

                                                                          \frac{d^2 I(z)}{d z^2}-\gamma^2 I(z)=0

两式表示用复数描述电压和电流的特性，其中系数 \gamma 是已知的复传播常数

                                                      \gamma = \alpha +j\beta=\sqrt{(R+j\omega L)(G+j\omega C)}

其中\alpha为衰减常数，\beta称为相位常数。

两式解都是指数函数，对于电压

                                                                       V(z)=V^+e^{-\gamma z}+V^- e^{+\gamma z}

对于电流

                                                                       I(z)=I^+e^{-\gamma z}+I^- e^{+\gamma z}

以上两式，第一项代表向+z方向传播的波，而第二项代表沿-z方向传播的波。这是没有实际意义的，因为\alpha\geq 0,所以\beta前的负号保证了+z方向传播的波的幅度将逐渐减小。同样，沿-z方向传播的波由于递减的指数项而逐渐衰减。

特性阻抗

将V(z)=V^+e^{-\gamma z}+V^- e^{+\gamma z}代入-\frac{d V(z)}{d z}=(R+j \omega L) I(z)   可得

                                                           I(z)=\frac{\gamma}{(R+j \omega L)}\left(V^{+} \mathrm{e}^{-\gamma z}-V^{-} \mathrm{e}^{+\gamma z}\right)

因为电压与电流通常通过阻抗联系起来，引入传输线的特性阻抗(characteristic impedance)Z_{0}，其定义为

                                                             Z_{0}=\frac{(R+j \omega L)}{\gamma}=\sqrt{\frac{(R+j \omega L)}{(G+j \omega C)}}

电流表达式可以写成

                                                               I(z)=\frac{1}{Z_{0}}\left(V^{+} \mathrm{e}^{-\gamma z}-V^{-} \mathrm{e}^{+\gamma z}\right)

Z_{0}并不是常规意义上的阻抗，它的定义是基于正向和反向行进的电压波和电流波。这与基于总电压，总电流概念定义的常规电路阻抗完全不同。

无损耗传输线模型

对于较短的线段，忽略损耗不会引起明显的误差，这意味着R=G=0,此时特征阻抗可简化为

                                                                                    Z_{0}=\sqrt{L/C}

如果选取参数为L和C的平行板传输线，那么其特性阻抗为

                                                                                    Z_{0}=\sqrt{\frac{\mu}{\epsilon}}\frac{d}{w}

其中，平方根项称为波阻抗，在自由空间(\mu=\mu_{0},\epsilon=\epsilon_{0})该值约为377\Omega。无损耗传输线的传播常数是纯虚数\gamma=j\beta，其中

\beta=\omega\sqrt{LC}。

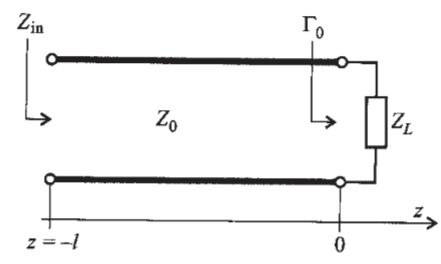
终端加载的无损耗传输线

电压反射系数

假定负载位于z=0处，电压波从z=-l处耦合入传输线。如下图

传输线方程与终端加载的无损耗传输线_第2张图片

已道，传输线上任意处的电压

                                                                        V(z)=V^+e^{-\gamma z}+V^- e^{+\gamma z}

上式第二项的物理意义是在z<0的区间，终端负载阻抗产生的反射。引入反射系数(reflection coefficient)\Gamma_{0},它是反射电压波与入射电压波在负载（z=0）处的比值：

                                                                                         \Gamma_{0}=\frac{V^-}{V^+}

根据这个定义，电压波和电流波游客用反射系数表示为

                                                                       V(z)=V^{+} (e^{-\gamma z}+\Gamma _{0} e^{+\gamma z})

和

                                                                       I(z)=\frac{V^{+}}{Z_{0}} (e^{-\gamma z}+\Gamma _{0} e^{+\gamma z})

如果用V(z)除以I(z)，可得沿着z轴-l\leq z\leq 0q区间内任意点处，作为空间函数的阻抗Z(z)的表达式。在z=-l处的总输入阻抗通常记为Z_{in}。在z=0处，阻抗等于负载阻抗：

                                                                           Z(0)=Z_{L}=Z_{0}\frac{1+\Gamma_{0}}{1-\Gamma_{0}}

可求出反射系数

                                                                                   \Gamma_{0}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}

上式更加常用，因为它只含已知电路参数，而与特定的电压波幅度之比无关。

当负载开路时Z_{L}=\infty，反射系数\Gamma_{0}=1，这意味着反射电压波与入射电压波有着相同的相位；

当负载短路时Z_{L}=0，反射系数\Gamma_{0}=-1，这意味着反射电压波与入射电压波有着相反的振幅；

当Z_{0}=Z_{L}(此时负载阻抗与传输线的特性阻抗相匹配),反射系数\Gamma_{0}=0，不发生反射，说明此时入射电压波完全被负载吸收了。

传播常数与相速度

对于无损耗的传输线R=G=0，复数传播常数的定义是具有非常简单的形式

                                                                            \gamma=\alpha+j\beta=j\omega\sqrt{LC}

其中，\alpha为衰减常数，\beta称为相位常数。且\alpha=0，\beta=\omega\sqrt{LC}。

此时

                                                                        V(z)=V^{+} (e^{-j\beta z}+\Gamma _{0} e^{+j\beta z})

                                                                         I(z)=\frac{V^{+}}{Z_{0}} (e^{-j\beta z}-\Gamma _{0} e^{+j\beta z})

相位常数与相速度的关系

                                                                                     \beta=\frac{\omega}{v_{p}}

则相速度v_{p}可由传输线参数 L 和 C 给出

                                                                                   v_{p}=\frac{1}{\sqrt{LC}}

由此可见传输线中相速度与频率无关。这表明了如果在传输线中传播的是脉冲信号，可以把脉冲分解为一些列频率谐波分量，而每个频率分量都以同一固定相速度传播。所以当原始脉冲到达不同的位置时，都能保持形状不变。这种现象叫做无色散(dispersion-free)传输。然而实际情况下常常要考虑相速度在某种程度上的频率相关性，或称色散，色散将引起信号畸变。

驻波与电压驻波比

把终端短路的传输线\Gamma_{0}=1放在新坐标系d中描述

传输线方程与终端加载的无损耗传输线_第3张图片

式V(z)=V^{+} (e^{-j\beta z}+\Gamma _{0} e^{+j\beta z})可改写成

                                                                      V(d)=V^{+}\left(e^{+j\beta d}-e^{-j\beta d}\right)

欧拉公式e^{ix}=cosx+isinx,上式括号中内容可改写为2jsin(\beta d),将上式从复数变换为时域形式得

                                                     \begin{aligned} v(d, t) &=\operatorname{Re}\left\{V e^{j \omega t}\right\}=\operatorname{Re}\left\{2 j V^{+} \sin (\beta d) e^{j \omega t}\right\} \\ &=2 V^{+} \sin (\beta d) \cos (\omega t+\pi / 2) \end{aligned}

其中，正弦项确保了在d=0处，任意时 t，电压都维持短路状态。c此时输入波与反射波的相位差是180\degree，导致波在空间位置为0，\lambda/2,\lambda,3\lambda/2等处出现了固定的爹加零点。

传输线方程与终端加载的无损耗传输线_第4张图片

将新坐标d引入V(z)=V^{+} (e^{-j\beta z}+\Gamma _{0} e^{+j\beta z}),该公式变为

                                                    V(d)=V^{+} e^{+j\beta d}(1+\Gamma_{0} e^{-2j\beta d})=A(d)[1+\Gamma(d)]

其中，设A(d)=V^{+} e^{+j\beta d}，并定义反射系数：

                                                                            \dpi{120} \Gamma(d)=\Gamma_{0} e^{-2j\beta d}

同理，在新的空间坐标系中，电流波的定义为

                                                    I(d)=\frac{V^{+}}{Z_{0}} e^{+j\beta z}(1-\Gamma_{0} e^{-2j\beta d})=\frac{A(d)}{Z_{0}}[1-\Gamma(d)]

在匹配条件下(\Gamma_{0}=0)，反射系数\Gamma(d)=0，此时只有向右传播的波。为了量化不匹配的程度，引入驻波比(standing wave ratio,SWR),又称驻波系数，即传输线上电压最大幅度(或电流)与电压最小幅度(或电流)的比值

                                                                           SWR=\frac{|V_{max}|}{|V_{min}|}=\frac{|I_{max}|}{|I_{min}|}

注意到\Gamma(d)的最大幅度是1，可将上式表示为下式

                                                                                    SWR=\frac{1+|\Gamma_{0}|}{1-|\Gamma_{0}|}

其取值范围是1\leq SWR\leq \infty。图像如下

传输线方程与终端加载的无损耗传输线_第5张图片

很多情况下，称SWR为电压驻波比(voltage standing wave ratio,VSWR)以区分功率驻波比(PSWR)。严格地说SWR只能运用于无损耗传输线，因为有损耗传输线电压与电流的幅值是距离的函数。但多数射频系统损耗很低，式SWR=\frac{1+|\Gamma_{0}|}{1-|\Gamma_{0}|}可以使用。观察\Gamma(d)=\Gamma_{0} e^{-2j\beta d}得，反射系数的实部(以及虚部)的最大最小值之间的距离为d=\lambda/4即2\beta d=\pi,最大值之间的距离是d=\lambda/2。

你可能感兴趣的:(射频电路)

  • rf 's book gtkknd rf
    微波射频工程师必读经典参考书更新于2013-08-0521:14:42文章出处:互联网微波射频工程师参考书EDA仿真设计《ADS应用详解--射频电路设计与仿真》『中』陈艳华、李朝晖、夏玮编著人民邮电出版社图书简介：本书介绍使用ADS进行射频电路设计和仿真的基础知识和方法。网友书评1：这本书50刀，不值得。作者估计不是射频专业人士，纯粹抄袭网上的那个9个经典实例，而且还有删减，加多了一个功分器，VC
  • 第一章、正交频分复用系统的基本原理-基于XILINX FPGA的OFDM通信系统基带设计 BinaryStarXin 通信射频相控阵-软硬技术提升篇fpga开发OFDM系统硬件工程驱动开发物联网嵌入式硬件stm32
    在信息时代的今天,通信技术在各种信息技术中起着支撑作用。人类社会对通信的需求越来越高,希望能够更加方便快捷地获取信息和进行沟通。因此,世界各国都在致力于现代通信技术的研究与开发和现代通信网的建设。而无线通信以其独特的便利性更是得到了人们的格外青睐。特别是在过去的十余年时间里,在数字信号处理、射频电路制造技术和半导体技术的推动下,无线通信获得了巨大的发展,便携移动设备变得更小、更便宜、更可靠。毫无疑
  • 西门子GPRS模块开发详解 GodQ C++GPRS模块使用平台outputinternet服务器网络service
    以模块MC55为例，MC55是SIEMENS(西门子)公司推出的GSM/GPRS三频模块，主要为语音传输、短消息和GPRS数据业务提供无线接口。MC55集成了完整的RF射频电路和GSM的基带处理器，十分适合开发一些基于GSM/GPRS的无线应用产品，如监控、调度、车载、遥控、远程测量、定位和导航等领域的系统和产品，应用范围十分广泛。用户只需投入少量的研发费用，就可以在较短的研发周期内集成自己的应用
  • 大功率UWB模块 XZM3000 移植手册 《从DWM1000到XZM3000移植手册》 xiongdauwb 超宽带射频模组熊大UWB系列教程大功率UWB模块超宽带测距定位超宽带模块
    DWM1000模组内部集成了DW1000芯片和相关射频电路，可以快速的用于开发测距和定位系统。但是DWM1000模组有个缺点就是通讯距离非常受限，6.8M波特率通讯距离30米，110K波特率通讯距离60米。在实际的工程中非常受限制，针对这种情况，博主公司开发了兼容DWM1000的大功率UWB模组，将测距距离提升到6.8M波特率400米/110K波特率600米的通讯距离，适合应用与实际工程场景。一、
  • 射频电路设计规范 兴风作浪的梦 电路设计及基本常识PCB设计下位机射频设计
    1、射频电路中元器件封装的注意事项成功的RF设计必须仔细注意整个设计过程中每个步骤及每个细节，这意味着必须在设计开始阶段就要进行彻底的、仔细的规划，并对每个设计步骤的进展进行全面持续的评估。而这种细致的设计技巧正是国内大多数电子企业文化所欠缺的。近几年来，由于蓝牙设备、无线局域网络(WLAN)设备，和移动电话的需求与成长，促使业者越来越关注RF电路设计的技巧。从过去到现在，RF电路板设计如同电磁干
  • 一种基于IWR6843雷达的跌倒检测系统的设计和实现(TI文档) 奔袭的算法工程师 雷达信号处理目标检测人工智能算法
    摘要随着年龄增长，人体各项生理机能退化严重，老年人很容易发生跌倒，导致身体受到严重的伤害。近年来，随着国内人口老龄化越来越严重，主要针对老年人的跌倒检测系统正受到越来越多的关注。和常用的加速度传感器和视觉技术相比，基于毫米波雷达的跌倒检测系统具有非接触式，全天候工作和隐私友好等优点，正受到越来越多的关注。TI的IWR6843是业内第一款基于RF-CMOS工艺，将中射频电路，VCO，ADC，DSP和
  • 无线电子产品前端射频设计注意事项 Aaron Mo 射频工程设计规范
    1引言1.1编写目的整理带无线的产品RF部分对外壳及PCBA设计注意事项，主要目的是为设计者提供一些参考，提高无线产品的设计质量和效率、保证可生产性。1.2背景RF布局是射频电路设计极为重要的步骤和环节，关系到射频信号能否有效的工作、产品性能是否达标、生产是否能顺利、使用是否安全等问题。本文以市面一些产品进行讲述一些设计注意事项，因这些产品都是采用模组形式，射频器件布局走线及天线设计净空本文就不讲
  • ADS微带单枝短截线匹配电路的仿真 秋风知我意i ADSADS电磁仿真
    ADS微带单枝短截线匹配电路的仿真简介环境原理图过程版图过程简介利用ADS2020软件设计匹配电路通常有5种方法，本小节首先介绍如何通过“Design-Guide”进行微带单枝短截线匹配电路的设计与仿真。环境ADS2020《ADS2011射频电路设计与仿真实例》[徐兴福著][电子工业出版社][2014.05]原理图过程新建工程，并创建一个原理图，点击菜单栏Insert=》Template=》ads
  • 射频电路设计——传输线理论(Transmission Line Analysis) 【下】 弱反型人类 射频电路设计模拟电子技术硬件电学
    射频电路设计(RFCircuitDesign)——传输线理论(TransmissionLineAnalysis)【下】上篇传输线理论(TransmissionLineAnalysis)【上】文章目录射频电路设计(RFCircuitDesign)——传输线理论(TransmissionLineAnalysis)【下】前言正文3️⃣终端加载的无损耗传输线模型(最基础的模型)4️⃣连接波源、负载的传输线
  • 整理笔记——射频基础知识 仲南音 电路基础电路基础
    一、什么是射频射频（RF），表示可以辐射到空间的电磁频率，频率范围从300kHz～300GHz之间。每秒变化小于1000次的交流电称为低频电流，大于10000次的交流电称为高频电流，射频就是高频交流变化的电磁波。处理信号的电磁波长与电路或元器件尺寸处于同一量级的电路成为射频电路。此时由于期间尺寸和导线的关系电路需用分布参数的相关理论处理。1.1阻抗的概念电阻与电抗在向量上的和称之为阻抗，在设计高频
  • 搞定蓝牙——第二篇(蓝牙架构) woniu2333 蓝牙技术蓝牙
    哪吒跑过去掰扯着她师傅手里的法宝，左看右看，嘴里嘟囔着，这叫蓝牙的法宝怎么这么厉害呢，怎么都看不明白。太乙真人笑眯眯的对她说，来吧，我带你走进蓝牙的时间，让你一窥里面的奥秘。。。蓝牙控制器与主机在上一篇中讲到了三种蓝牙方案，蓝牙技术是包含了硬件芯片、软件程序。蓝牙硬件部分就是射频电路部分，最基本的功能就是将数字信号转换成电磁波发送出去。软件部分要实现的就是将用户要发送的数据按照一定的协议格式封包发
  • 射频电路设计的常见问题及经验总结 EDA365电子论坛 RF射频RF硬件
    一什么是射频电路射频简称RF，射频就是射频电流，它是一种高频交流变化电磁波的简称。每秒变化小于1000次的交流电称为低频电流，大于1000次的称为高频电流，而射频就是这样一种高频电流。射频电路指处理信号的电磁波长与电路或器件尺寸处于同一数量级的电路。此时由于器件尺寸和导线尺寸的关系，电路需要用分布参数的相关理论来处理，这类电路都可以认为是射频电路，对其频率没有严格要求，如长距离传输的交流输电线（5
  • AT2402E替代RFX2402E射频前端芯片_PA芯片 dnsj5343 RFID
    AT2402E是一款应用于无线通信的集成收发功能的射频前端单芯片，芯片内部集成了所需要的射频电路模块，集成度非常高，主要包括功率放大器(PA)，低噪声放大器(LNA)，收发模式切换的开关控制电路等电路子模块。AT2402E集成了简单的低压控制逻辑电路，可以使用工作系统内较低的基带电压来控制芯片的工作模式。芯片内部集成了天线端口，发射端口以及接收端口的射频阻抗匹配电路，可以不需要重新设计芯片的外围阻
  • AT2402E射频前端单芯片替代RFX2402E dnsj5343 物联网IOT芯片
    AT2402E是一款应用于无线通信的集成收发功能的射频前端单芯片，芯片内部集成了所需要的射频电路模块，集成度非常高，主要包括功率放大器(PA)，低噪声放大器(LNA)，收发模式切换的开关控制电路等电路子模块。芯片集成了简单的低压控制逻辑电路，可以使用工作系统内较低的基带电压来控制芯片的工作模式。芯片内部集成了天线端口，发射端口以及接收端口的射频阻抗匹配电路，可以不需要重新设计芯片的外围阻抗电路。芯
  • AT2402E 完美替代RFX2402E无线通信集成收发功能射频前端功放单芯片 weng13924672287 PA功放单片机mcustm32射频工程智能电视
    AT2402E是一款应用于无线通信的集成收发功能的射频前端单芯片，芯片内部集成了所需要的射频电路模块，集成度非常高，主要包括功率放大器(PA)，低噪声放大器(LNA)，收发模式切换的开关控制电路等电路子模块。芯片集成了简单的低压控制逻辑电路，可以使用工作系统内较低的基带电压来控制芯片的工作模式。芯片内部集成了天线端口，发射端口以及接收端口的射频阻抗匹配电路，可以不需要重新设计芯片的外围阻抗电路。芯
  • AT2402E 完美替代 RFX2402E 无线通信集成收发功能射频前端功放单芯片 weng13924672287 PA功放单片机物联网stm32mcu智能电视
    AT2402E是一款应用于无线通信的集成收发功能的射频前端单芯片，芯片内部集成了所需要的射频电路模块，集成度非常高，主要包括功率放大器(PA)，低噪声放大器(LNA)，收发模式切换的开关控制电路等电路子模块。芯片集成了简单的低压控制逻辑电路，可以使用工作系统内较低的基带电压来控制芯片的工作模式。芯片内部集成了天线端口，发射端口以及接收端口的射频阻抗匹配电路，可以不需要重新设计芯片的外围阻抗电路。芯
  • 手机芯片基带芯片及服务器芯片有什么区别,手机射频电路知识干货，射频芯片和基带芯片又是什么关系？... 稻草人旅行
    原标题：手机射频电路知识干货，射频芯片和基带芯片又是什么关系？1.手机射频工作原理与电路分析2.图解手机射频电路的设计原理及应用3.手机里的射频芯片和基带芯片是什么关系？图解手机射频电路的设计原理及应用一、射频电路组成和特点：普通手机射频电路由接收通路、发射通路、本振电路三大电路组成。其主要负责接收信号解调;发射信息调制。早期手机通过超外差变频(手机有一级、二级混频和一本、二本振电路)，后才解调出
  • 【射频电路基础】第二章-谐振功率放大器 xxxflower. 射频电路基础射频工程信息与通信
    本书所用版本为:《射频电路基础》第二版（赵建勋邓军著）网课详情见b站:《射频电路基础（高频电子线路）》本书的笔记以书本和手写笔记结合为主。文章目录第二章谐振功率放大器1.谐振功率放大器的工作原理2.谐振功率放大器的工作状态第三章正弦波振荡器1.反馈式振荡器的基本原理2.LC正弦波振荡器电路第二章谐振功率放大器1.谐振功率放大器的工作原理2.谐振功率放大器的工作状态第三章正弦波振荡器1.反馈式振荡器
  • 《ADS2011射频电路设计与仿真实例》功率放大器设计的输入输出匹配 程序源_hytz ads学习ads射频徐兴福smith圆图匹配低Q值匹配
    徐兴福这本书的6.6Smith圆图匹配这一节中具体匹配时，直接给出了电容与串联微带的值，没有给出推导过程，我一开始以为是省略了详细推导过程，后来发现好像基本上是可以随便自己设的。以输入匹配（书本6.6.4输入匹配电路的建立）为例：因为它这里要求要在Q=1.5的等Q圆里面进行匹配，可以按照书本的操作显示出1.5的等Q圆，如图1所示：图1：红线为Q=1.5的等Q圆我们知道，模块的带宽和Q值是成反比的，
  • WiFi产品的一般射频电路设计 恋风恋歌的干货铺 嵌入式
    写在前面的话：这篇文章是我结合多年的工作经验和实践编写而成的，具有一定的实用性，希望能够对大家的设计工作起到一定的帮助作用。I.前言这是一篇针对性很强的技术文章。在这篇文章中，我只是分析研究了Wi-Fi产品的一般射频电路设计，而且主要分析的是Atheros和Ralink的解决方案，对于其他厂商的解决方案并没有进行研究。这是一篇针对性很不强的技术文章。在这篇文章中，我研究，讨论了Wi-Fi产品中的射
  • 12、ADS使用记录之功分器设计 怡步晓心l 电磁领域电磁学
    12、ADS使用记录之功分器设计基于ADS2022参考的书籍是卢益锋老师的ADS射频电路设计与仿真学习笔记前置教程：01、ADS使用记录之新建工程02、ADS使用记录之导入各类仿真模型导入03、ADS使用记录之DC仿真控制器的使用04、ADS使用记录之S仿真控制器的使用&椭圆低通滤波器设计05、ADS使用记录之集总参数匹配06、ADS使用记录之分布式参数匹配07、ADS使用记录之匹配Q值-宽带与窄
  • 《ADS2011射频电路设计与仿真实例》第一章—第六章用ads2017跟做的不同操作 程序源_hytz ads学习ads信息与通信射频射频工程
    我用的是ads2017，可能是因为版本原因，有些操作和书上的不一样1.P69Smithchartutility中，若要调节各曲线圆系的线条颜色，书上写的“执行菜单命令【circles】→【colors】”应该是【view】→【colors】2.P83要用微带线，书上写的在原理图设计窗口的面板列表中选择“DG-MicrostripCircuits”，但是前面还有个“PassiveCircuit...
  • 26、ADS瞬时波形仿真-TRANSIENT仿真（以共射放大器为例） 怡步晓心l 射频功率放大器设计电磁领域硬件工程5G网络
    26、ADS瞬时波形仿真-TRANSIENT仿真（以共射放大器为例）在本科期间，学习模电的时候总是要对各种三极管电路进行MULTISIM仿真，其实ADS具备相同的功能，而且对于射频电路，使用ADS进行仿真可以结合版图进行，在此介绍其级别仿真方法。工程如下：https://download.csdn.net/download/weixin_44584198/883072761.设计指标电压放大倍数：
  • 系统级封装（SiP）技术如何助力智能化应用发展呢？ aibotest 人工智能服务器
    智能化时代，各种智能设备、智能互连的高速发展与跨界融合，需要高密度、高性能的微系统集成技术作为重要支撑。例如，在系统级封装（SiP）技术的加持下，5G手机的射频电路面积更小，但支持的频段更多。射频前端（RFFE）、低功耗蓝牙、WiFi、雷达（Radar）、传感器（Sensor）、电源管理芯片（PMIC）、存储（Memory）等半导体器件，在智能手机、5G通讯、工业、智能交通等领域已得到广泛应用，S
  • 射频入门知识-1 SofterICer 射频算法机器学习人工智能
    信号源示波器综合测试仪功率计噪声测试仪频谱分析仪频谱分析仪:放大器的噪声系数测试放大器增益测试噪声和增益是放大器的最关键指标，学学怎么用频谱仪做放大器的噪声测试那个hbf740输入和输出阻抗匹配具体怎么搞《ADS2011射频电路设计与仿真实例》【徐兴福著】【电子工业出版社】，里边有55143输入输出阻抗匹配的讲解，于740几乎相同，过程十分详细
  • 前沿分享-中距离射频取电 大饼酱人 非技术篇单片机
    目前来看，微能源有四种技术路线，一是环境光采集、温差转换采集、无线射频采集和振动能量采集。无线射频微能源是在通信设备通信过程中自然产生的，可以通过射频能量芯片实现无线射频取电，能瞬间大功率储电和安全驱动负载。通过射频电路将电能转化成通信所需的其他能量。可实现在中远距离通信环境中，让不带电池或不接电源线的接收端设备，获得和收集一定距离范围内的无线射频信号，并将其转化成可持续电流。找资料的时候发现这家
  • 简单射频常识 wy-2021
    1.射频电路的基本特点:处理的信号都为高频信号，随着工作频率的升高，电磁波的波长变短，当相应波长与电路元件相比拟时，电容电阻电感的电学特性偏离理想频率响应。2.高频选频放大器，滤波器，混频器选频放大器具有选择特定频率并放大的功能；利用谐振电路进行选频，只有在谐振频率时，电路阻抗最低，电流最大。滤波器：运行相应带宽频率通过，其他频率段信号受到抑制。利用电容与电感的性质（高频电容通过电感断，低频电感通
  • 01、滤波器设计——LC滤波器设计 冬冬甜甜枪 #滤波器射频工程
    1、原理LC滤波器：由集总LC组成的滤波器。适用于3Ghz以下的应用。体积小，便于安装，无寄生通带，设计灵活。而由于电感元件Q值较低，不宜在高矩形度、低插入损耗（S21）、窄带情况下使用。1.1、主要参数指标（1）RF插入损耗：在理想情况下，插入到射频电路中的理想滤波器，不应在其通带内引入任何功率损耗。然而，在现实中，我们无法消除滤波器固有的、某种程度的功率损耗。插入损耗定量地描述了功率响应幅度与
  • 射频通信接收机设计的主要结构 32RayZer 网络
    【导读】在一个射频通信系统中，噪声，尤其是信噪比（SNR），是无线接收机中的一个基本问题。高噪声电平会限制系统的容量、覆盖范围，以及许多对系统运营商和终端用户都有重大影响的相关特性。射频通信接收机是射频电路中比较重要的一部分，射它能在频信号经天线接收后，经过相关滤波器和放大器，将射频信号进行一系列的频率变化，最终将信号调节成所需要的调制信号。在一个射频通信系统中，噪声，尤其是信噪比（SNR），是无
  • 11、ADS使用记录之LNA设计 怡步晓心l 电磁领域电磁学
    11、ADS使用记录之LNA设计基于ADS2022参考的书籍是卢益锋老师的ADS射频电路设计与仿真学习笔记前置教程：01、ADS使用记录之新建工程02、ADS使用记录之导入各类仿真模型导入03、ADS使用记录之DC仿真控制器的使用04、ADS使用记录之S仿真控制器的使用&椭圆低通滤波器设计05、ADS使用记录之集总参数匹配06、ADS使用记录之分布式参数匹配07、ADS使用记录之匹配Q值-宽带与窄
  • eclipse maven IXHONG eclipse
    eclipse中使用maven插件的时候，运行run as maven build的时候报错 -Dmaven.multiModuleProjectDirectory system propery is not set. Check $M2_HOME environment variable and mvn script match.   可以设一个环境变量M2_HOME指
  • timer cancel方法的一个小实例 alleni123 多线程timer
    package com.lj.timer; import java.util.Date; import java.util.Timer; import java.util.TimerTask; public class MyTimer extends TimerTask { private int a; private Timer timer; pub
  • MySQL数据库在Linux下的安装 ducklsl mysql
    1.建好一个专门放置MySQL的目录 /mysql/db数据库目录 /mysql/data数据库数据文件目录 2.配置用户，添加专门的MySQL管理用户 >groupadd mysql ----添加用户组 >useradd -g mysql mysql ----在mysql用户组中添加一个mysql用户 3.配置，生成并安装MySQL >cmake -D
  • spring------>>cvc-elt.1: Cannot find the declaration of element Array_06 springbean
    将-------- <?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans"     xmlns:xsi="http://www.w3
  • maven发布第三方jar的一些问题 cugfy maven
    maven中发布 第三方jar到nexus仓库使用的是 deploy:deploy-file命令 有许多参数，具体可查看 http://maven.apache.org/plugins/maven-deploy-plugin/deploy-file-mojo.html 以下是一个例子： mvn  deploy:deploy-file -DgroupId=xpp3
  • MYSQL下载及安装 357029540 mysql
        好久没有去安装过MYSQL，今天自己在安装完MYSQL过后用navicat for mysql去厕测试链接的时候出现了10061的问题，因为的的MYSQL是最新版本为5.6.24，所以下载的文件夹里没有my.ini文件，所以在网上找了很多方法还是没有找到怎么解决问题，最后看到了一篇百度经验里有这个的介绍，按照其步骤也完成了安装，在这里给大家分享下这个链接的地址
  • ios TableView cell的布局 张亚雄 tableview
      cell.imageView.image = [UIImage imageNamed:[imageArray objectAtIndex:[indexPath row]]];           CGSize itemSize = CGSizeMake(60, 50);   &nbs
  • Java编码转义 adminjun java编码转义
    import java.io.UnsupportedEncodingException; /** * 转换字符串的编码 */ public class ChangeCharset { /** 7位ASCII字符，也叫作ISO646-US、Unicode字符集的基本拉丁块 */ public static final Strin
  • Tomcat 配置和spring aijuans spring
    简介 Tomcat启动时，先找系统变量CATALINA_BASE，如果没有，则找CATALINA_HOME。然后找这个变量所指的目录下的conf文件夹，从中读取配置文件。最重要的配置文件：server.xml 。要配置tomcat，基本上了解server.xml，context.xml和web.xml。 Server.xml --  tomcat主
  • Java打印当前目录下的所有子目录和文件 ayaoxinchao 递归File
    其实这个没啥技术含量，大湿们不要操笑哦，只是做一个简单的记录，简单用了一下递归算法。   import java.io.File; /** * @author Perlin * @date 2014-6-30 */ public class PrintDirectory { public static void printDirectory(File f
  • linux安装mysql出现libs报冲突解决 BigBird2012 linux
    linux安装mysql出现libs报冲突解决 安装mysql出现 file /usr/share/mysql/ukrainian/errmsg.sys from install of MySQL-server-5.5.33-1.linux2.6.i386 conflicts with file from package mysql-libs-5.1.61-4.el6.i686  
  • jedis连接池使用实例 bijian1013 redisjedis连接池jedis
    实例代码： package com.bijian.study; import java.util.ArrayList; import java.util.List; import redis.clients.jedis.Jedis; import redis.clients.jedis.JedisPool; import redis.clients.jedis.JedisPoo
  • 关于朋友 bingyingao 朋友兴趣爱好维持
      成为朋友的必要条件：    志相同，道不合，可以成为朋友。譬如马云、周星驰一个是商人，一个是影星，可谓道不同，但都很有梦想，都要在各自领域里做到最好，当他们遇到一起，互相欣赏，可以畅谈两个小时。     志不同，道相合，也可以成为朋友。譬如有时候看到两个一个成绩很好每次考试争做第一，一个成绩很差的同学是好朋友。他们志向不相同，但他
  • 【Spark七十九】Spark RDD API一 bit1129 spark
    aggregate package spark.examples.rddapi import org.apache.spark.{SparkConf, SparkContext} //测试RDD的aggregate方法 object AggregateTest { def main(args: Array[String]) { val conf = new Spar
  • ktap 0.1 released bookjovi kerneltracing
    Dear, I'm pleased to announce that ktap release v0.1, this is the first official release of ktap project, it is expected that this release is not fully functional or very stable and we welcome bu
  • 能保存Properties文件注释的Properties工具类 BrokenDreams properties
            今天遇到一个小需求：由于java.util.Properties读取属性文件时会忽略注释，当写回去的时候，注释都没了。恰好一个项目中的配置文件会在部署后被某个Java程序修改一下，但修改了之后注释全没了，可能会给以后的参数调整带来困难。所以要解决这个问题。     &nb
  • 读《研磨设计模式》-代码笔记-外观模式-Facade bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /* * 百度百科的定义： * Facade（外观）模式为子系统中的各类（或结构与方法）提供一个简明一致的界面， * 隐藏子系统的复杂性，使子系统更加容易使用。他是为子系统中的一组接口所提供的一个一致的界面 * * 可简单地
  • After Effects教程收集 cherishLC After Effects
    1、中文入门 http://study.163.com/course/courseMain.htm?courseId=730009 2、videocopilot英文入门教程（中文字幕） http://www.youku.com/playlist_show/id_17893193.html 英文原址： http://www.videocopilot.net/basic/ 素
  • Linux Apache 安装过程 crabdave apache
    Linux Apache 安装过程   下载新版本： apr-1.4.2.tar.gz（下载网站：http://apr.apache.org/download.cgi） apr-util-1.3.9.tar.gz（下载网站：http://apr.apache.org/download.cgi） httpd-2.2.15.tar.gz（下载网站：http://httpd.apac
  • Shell学习 之 变量赋值和引用 daizj shell变量引用赋值
    本文转自：http://www.cnblogs.com/papam/articles/1548679.html Shell编程中，使用变量无需事先声明，同时变量名的命名须遵循如下规则： 首个字符必须为字母（a-z，A-Z） 中间不能有空格，可以使用下划线（_） 不能使用标点符号 不能使用bash里的关键字（可用help命令查看保留关键字） 需要给变量赋值时，可以这么写：
  • Java SE 第一讲（Java SE入门、JDK的下载与安装、第一个Java程序、Java程序的编译与执行） dcj3sjt126com javajdk
    Java SE 第一讲： Java SE：Java Standard Edition Java ME: Java Mobile Edition Java EE：Java Enterprise Edition Java是由Sun公司推出的（今年初被Oracle公司收购）。 收购价格：74亿美金 J2SE、J2ME、J2EE JDK：Java Development
  • YII给用户登录加上验证码 dcj3sjt126com yii
    1、在SiteController中添加如下代码： /** * Declares class-based actions. */ public function actions() { return array( // captcha action renders the CAPTCHA image displ
  • Lucene使用说明 dyy_gusi Lucenesearch分词器
    Lucene使用说明 1、lucene简介 1.1、什么是lucene     Lucene是一个全文搜索框架，而不是应用产品。因此它并不像baidu或者googleDesktop那种拿来就能用，它只是提供了一种工具让你能实现这些产品和功能。 1.2、lucene能做什么     要回答这个问题，先要了解lucene的本质。实际
  • 学习编程并不难,做到以下几点即可! gcq511120594 数据结构编程算法
    不论你是想自己设计游戏，还是开发iPhone或安卓手机上的应用，还是仅仅为了娱乐，学习编程语言都是一条必经之路。编程语言种类繁多，用途各 异，然而一旦掌握其中之一，其他的也就迎刃而解。作为初学者，你可能要先从Java或HTML开始学，一旦掌握了一门编程语言，你就发挥无穷的想象，开发 各种神奇的软件啦。 1、确定目标 学习编程语言既充满乐趣，又充满挑战。有些花费多年时间学习一门编程语言的大学生到
  • Java面试十问之三：Java与C++内存回收机制的差别 HNUlanwei javaC++finalize()堆栈内存回收
    大家知道， Java 除了那 8 种基本类型以外，其他都是对象类型（又称为引用类型）的数据。 JVM 会把程序创建的对象存放在堆空间中，那什么又是堆空间呢？其实，堆（ Heap）是一个运行时的数据存储区，从它可以分配大小各异的空间。一般，运行时的数据存储区有堆（ Heap）和堆栈（ Stack），所以要先看它们里面可以分配哪些类型的对象实体，然后才知道如何均衡使用这两种存储区。一般来说，栈中存放的
  • 第二章 Nginx+Lua开发入门 jinnianshilongnian nginxlua
    Nginx入门 本文目的是学习Nginx+Lua开发，对于Nginx基本知识可以参考如下文章： nginx启动、关闭、重启 http://www.cnblogs.com/derekchen/archive/2011/02/17/1957209.html agentzh 的 Nginx 教程 http://openresty.org/download/agentzh-nginx-tutor
  • MongoDB windows安装 基本命令 liyonghui160com
      windows安装    安装目录：   D:\MongoDB\   新建目录   D:\MongoDB\data\db   4.启动进城：   cd D:\MongoDB\bin   mongod -dbpath D:\MongoDB\data\db   &n
  • Linux下通过源码编译安装程序 pda158 linux
    一、程序的组成部分 　　Linux下程序大都是由以下几部分组成： 　　二进制文件：也就是可以运行的程序文件 　　库文件：就是通常我们见到的lib目录下的文件 　　配置文件：这个不必多说，都知道 　　帮助文档：通常是我们在linux下用man命令查看的命令的文档 　　 二、linux下程序的存放目录 　　linux程序的存放目录大致有三个地方： 　　/etc, /b
  • WEB开发编程的职业生涯４个阶段 shw3588 编程Web工作生活
    觉得自己什么都会 2007年从学校毕业，凭借自己原创的ASP毕业设计，以为自己很厉害似的，信心满满去东莞找工作，找面试成功率确实很高，只是工资不高，但依旧无法磨灭那过分的自信，那时候什么考勤系统、什么OA系统、什么ERP，什么都觉得有信心，这样的生涯大概持续了约一年。 根本不是自己想的那样 2008年开始接触很多工作相关的东西，发现太多东西自己根本不会，都需要去学，不管是asp还是js，
  • 遭遇jsonp同域下变作post请求的坑 vb2005xu jsonp同域post
    今天迁移一个站点时遇到一个坑爹问题,同一个jsonp接口在跨域时都能调用成功,但是在同域下调用虽然成功,但是数据却有问题. 此处贴出我的后端代码片段 $mi_id = htmlspecialchars(trim($_GET['mi_id '])); $mi_cv = htmlspecialchars(trim($_GET['mi_cv ']));  贴出我前端代码片段: $.aj
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他