一天一大 leet(不同路径 II)难度:中等-Day20200706

题目:

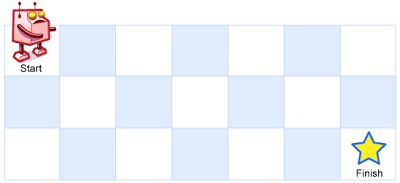
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

说明

m 和 n 的值均不超过 100。

示例

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

抛砖引玉

先计算没有障碍物时从一个位置到另外一个位置的方式
思路

• obstacleGrid 长 m，每个子集长 n
• 借助 m 和 n，生产一个 m*n 的数组(矩阵)
• 来迭代这个矩阵，从[0][0]到[m][n]
• 设 i 是 m 中的指针，j 是 n 中的指针，迭代过程中每一个[i][j]的变化都会生成一个新的路线
• 那迭代时把前面出现的可能都累加到[i][j]，那么[m - 1][n - 1]就是想要查找的可能数

实现

• 因为迭代过程中每一个[i][j]的变化都会生成一个新的路线那么默认矩阵中每个节点的值都为 1，代表一种可能

var uniquePaths = function (obstacleGrid) {
  let m = obstacleGrid.length,
    n = obstacleGrid[0] ? obstacleGrid[0].length : 0,
    cur = Array(m).fill(Array(n).fill(1))
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      cur[i][j] += cur[i][j - 1]
    }
  }
  return cur[m - 1][n - 1]
}

观察上面的逻辑会发下，迭代时涉及计算都是在单行中进行及 i 不变
那么尝试对矩阵降维，只记录结束值到这一列看下，优化：

var uniquePaths = function (obstacleGrid) {
  let m = obstacleGrid.length,
    n = obstacleGrid[0] ? obstacleGrid[0].length : 0,
    cur = Array(n).fill(1)
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      cur[j] += cur[j - 1]
    }
  }
  return cur[n - 1]
}

---

回到本题，如果遇到障碍：

• 假设障碍位置就是终点那到达这个位置的方式不存在，就是 0 即 cur[j] = 0
• 如果存在路径，起点也不能是障碍
• 当指针在某一列 j，其上一步如果是障碍，那到达这边的可能也是 0
  • 到达某一个位置理论上都要两种方式，一种方式一种方式的判断

/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function (obstacleGrid) {
  let m = obstacleGrid.length,
    n = obstacleGrid[0] ? obstacleGrid[0].length : 0,
    cur = Array(m).fill(0)
  cur[0] = obstacleGrid[0][0] == 0 ? 1 : 0
  for (let i = 0; i < m; ++i) {
    for (let j = 0; j < n; ++j) {
      // 遇到障碍
      if (obstacleGrid[i][j] === 1) {
        cur[j] = 0
      } else if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
        cur[j] += cur[j - 1]
      }
    }
  }
  return cur[n - 1]
}

如果上面只记录目的地是列的逻辑不易理解的话，再升维，来个直观的方式：
cur[i][j]记录从 cur[0][0]到其的所有方式

/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function (obstacleGrid) {
  let m = obstacleGrid.length,
    n = obstacleGrid[0] ? obstacleGrid[0].length : 0,
    cur = Array(m).fill(Array(n).fill(0))
  // 起点不能为障碍
  cur[0][0] = obstacleGrid[0][0] == 0 ? 1 : 0
  for (let i = 0; i < m; ++i) {
    for (let j = 0; j < n; ++j) {
      // 遇到障碍
      if (obstacleGrid[i][j] === 1) {
        cur[i][j] = 0
      } else if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
        // 上一步不是障碍
        cur[i][j] += cur[i][j - 1]
      }
    }
  }
  return cur[m - 1][n - 1]
}

上面方法与官方答案逻辑一致

留下官方讲解：官方答案

其他解法

基准行列

• 走到[i][j] ，要么是从左边的点过来的，要么是从上边的点过来的

• 到达[i][j]的方式数 = 到达[i−1][j]的方式数 + 到达[i][j-1]的方式数：
  cur[i][j] = cur[i−1][j] +cur[i][j-1]

• 可见，可以用自上而下的递归，也可以用自下而上的 cur：
  用 cur[i][j] 去记录子问题（对应递归就是子调用）的解

• 遇到障碍说明该点无法到达，方式归 0

注意：

• 基准中存在 i-1，j-1，如果还从 0 开始查询比较过程会越界
• 从 1 开始查询需要先初始化第一行第一列的基准

原题解

/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function (obstacleGrid) {
  if (obstacleGrid[0][0] == 1) return 0

  let m = obstacleGrid.length,
    n = obstacleGrid[0] ? obstacleGrid[0].length : 0,
    cur = Array(m)
  for (let i = 0; i < m; i++) cur[i] = Array(n)

  // 初始化起点
  cur[0][0] = 1
  for (let i = 1; i < m; i++) {
    // 初始化基准列：第一列
    cur[i][0] = obstacleGrid[i][0] == 1 || cur[i - 1][0] == 0 ? 0 : 1
  }
  for (let j = 1; j < n; j++) {
    // 初始化基准行：第一列
    cur[0][j] = obstacleGrid[0][j] == 1 || cur[0][j - 1] == 0 ? 0 : 1
  }
  // 迭代
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      cur[i][j] = obstacleGrid[i][j] == 1 ? 0 : cur[i - 1][j] + cur[i][j - 1]
    }
  }
  return cur[m - 1][n - 1]
}

总结

本题重点：

• 障碍位的方式数
• 记录指针在不同位置是存在的方式

另外上面两种解法:

1. 拿[0][0]做起始的基准点
2. 拿首行首列做基准点

的主要逻辑都是，下一次的结果从上次结果中推导出来。

也刷了不少动态规划的题，会发现：
动态规范适用的类型是，题目的逻辑可以查分成 n 个子逻辑的判断，而且子逻辑的结果之间还存在可以推导的关系

• 本题到达一个位置的方式可以通过上一个位置推导出来，刚好符合动态规划的逻辑

博客: 小书童博客

公号: 坑人的小书童