LeetCode 第 197 场周赛(468/5273,前8.88%)
文章目录
- 1. 比赛结果
- 2. 题目
- 1. LeetCode 5460. 好数对的数目 easy
- 2. LeetCode 5461. 仅含 1 的子串数 medium
- 3. LeetCode 5211. 概率最大的路径 medium(Dijkstra)
- 4. LeetCode 5463. 服务中心的最佳位置 hard(最优化退火算法)
1. 比赛结果
第三题一个地方的数组长度写错,浪费了好多时间,成绩应该可以再往前靠一下的,第四题数学最优化问题,不会。这是目前最好成绩 8.88%,继续加油!
全国排名: 468 / 5273,8.88%;全球排名: 0 / 1,00.0%

2. 题目
1. LeetCode 5460. 好数对的数目 easy
题目链接
给你一个整数数组 nums 。
如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ,就可以认为这是一组 好数对 。
返回好数对的数目。
示例 1:
输入:nums = [1,2,3,1,1,3]
输出:4
解释:有 4 组好数对,分别是 (0,3), (0,4), (3,4), (2,5) ,下标从 0 开始
示例 2:
输入:nums = [1,1,1,1]
输出:6
解释:数组中的每组数字都是好数对
示例 3:
输入:nums = [1,2,3]
输出:0
提示:
1 <= nums.length <= 100
1 <= nums[i] <= 100
解题:
- 直接暴力模拟
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
int n = nums.size(), i, j, sum = 0;
for(int i = 0; i < n; ++i)
{
for(j = i+1; j < n; ++j)
if(nums[i] == nums[j])
sum++;
}
return sum;
}
};
2. LeetCode 5461. 仅含 1 的子串数 medium
题目链接
给你一个二进制字符串 s(仅由 ‘0’ 和 ‘1’ 组成的字符串)。
返回所有字符都为 1 的子字符串的数目。
由于答案可能很大,请你将它对 10^9 + 7 取模后返回。
示例 1:
输入:s = "0110111"
输出:9
解释:共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次
示例 2:
输入:s = "101"
输出:2
解释:子字符串 "1" 在 s 中共出现 2 次
示例 3:
输入:s = "111111"
输出:21
解释:每个子字符串都仅由 '1' 组成
示例 4:
输入:s = "000"
输出:0
提示:
s[i] == '0' 或 s[i] == '1'
1 <= s.length <= 10^5
解题:
- 找到连续为1的个数,该区间内的符合要求的子串个数为 n ∗ ( n + 1 ) / 2 n*(n+1)/2 n∗(n+1)/2
class Solution {
public:
int numSub(string s) {
int i,j,n=s.size(),sum = 0, mod = int(1e9+7);
for(i = 0; i < n; ++i)
{
if(s[i]=='1')
{
j = i;
while(j < n && s[j]=='1')
{
j++;
}
long long n = j-i;
sum = (sum+((n*(n+1)/2)%mod))%mod;
i = j-1;
}
}
return sum%mod;
}
};
3. LeetCode 5211. 概率最大的路径 medium(Dijkstra)
题目链接
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,
其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。
只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
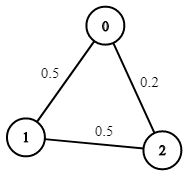
输入:n = 3, edges = [[0,1],[1,2],[0,2]],
succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,
而另一条为 0.5 * 0.5 = 0.25
输入:n = 3, edges = [[0,1],[1,2],[0,2]],
succProb = [0.5,0.5,0.3], start = 0, end = 2
输出:0.30000
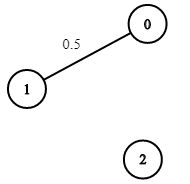
输入:n = 3, edges = [[0,1]],
succProb = [0.5], start = 0, end = 2
输出:0.00000
解释:节点 0 和 节点 2 之间不存在路径
提示:
2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边
解题:
- 迪杰斯特拉 最短路径+优先队列优化
struct cmp
{
bool operator()(const pair<int,double>& a, const pair<int,double>& b)const
{
return a.second < b.second;//概率大的优先
}
};
class Solution {
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
unordered_map<int,unordered_map<int,double>> m;
for(int i = 0; i < edges.size(); ++i)
{
m[edges[i][0]][edges[i][1]] = succProb[i];
m[edges[i][1]][edges[i][0]] = succProb[i];
}
vector<double> prob(n,0.0);
prob[start] = 1.0;
priority_queue<pair<int,double>,vector<pair<int,double>>,cmp> q;
q.push({start, 1.0});
while(!q.empty())
{
int i = q.top().first, j;
double p = q.top().second, pij;
q.pop();
for(auto it = m[i].begin(); it != m[i].end(); ++it)
{
j = it->first;
pij = it->second;
if(p*pij > prob[j])
{
prob[j] = p*pij;
q.push({j, prob[j]});
}
}
}
return prob[end];
}
};
4. LeetCode 5463. 服务中心的最佳位置 hard(最优化退火算法)
题目链接
一家快递公司希望在新城市建立新的服务中心。
公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和 。
换句话说,请你为服务中心选址,该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值:
∑ i = 0 n − 1 ( x centre − x i ) 2 + ( y centre − y i ) 2 \sum_{i=0}^{n-1} \sqrt{\left(x_{\text {centre}}-x_{i}\right)^{2}+\left(y_{\text {centre}}-y_{i}\right)^{2}} i=0∑n−1(xcentre−xi)2+(ycentre−yi)2
与真实值误差在 10^-5 之内的答案将被视作正确答案。
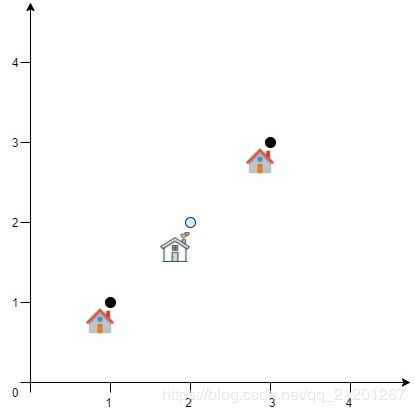
输入:positions = [[0,1],[1,0],[1,2],[2,1]]
输出:4.00000
解释:如图所示,你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置,
这样一来到每个客户的距离就都是 1,所有距离之和为 4 ,这也是可以找到的最小值。
输入:positions = [[1,1],[3,3]]
输出:2.82843
解释:欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
示例 3:
输入:positions = [[1,1]]
输出:0.00000
示例 4:
输入:positions = [[1,1],[0,0],[2,0]]
输出:2.73205
解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,
但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ,距离总和将会变为 2.73205
当心精度问题!
示例 5:
输入:positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出:32.94036
解释:你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置
提示:
1 <= positions.length <= 50
positions[i].length == 2
0 <= positions[i][0], positions[i][1] <= 100
解题:
- 参考第二名大佬的答案写的
- 大家说是退火算法,动态调整下一次迭代的步长,又有证明目标是凸函数,局部最小值就是全局最小值
class Solution {
public:
double getMinDistSum(vector<vector<int>>& positions) {
int n = positions.size(), k;
double x0, y0, xi = 0, yi = 0, nx, ny;
for(int i = 0; i < n; ++i)
{
xi += positions[i][0];
yi += positions[i][1];
}
x0 = xi/n;
y0 = yi/n;//均值作为初始值
vector<vector<int>> dir = {{1,0},{0,1},{0,-1},{-1,0}};
double eps = 1e-6, step = 100, d, dis = calSumDis(x0,y0,positions);
while(step > eps)
{
bool down = false;
for(k = 0; k < 4; ++k)
{
nx = x0 + dir[k][0]*step;
ny = y0 + dir[k][1]*step;
d = calSumDis(nx, ny, positions);
if(d < dis)
{
dis = d;
x0 = nx;
y0 = ny;
down = true;
break;
}
}
if(!down)//没有降低,说明步长太大
step /= 2.0;
}
return dis;
}
double calSumDis(double x0, double y0, vector<vector<int>>& p)
{
double d = 0.0;
for(auto& pi : p)
d += sqrt((x0-pi[0])*(x0-pi[0])+(y0-pi[1])*(y0-pi[1]));
return d;
}
};
20 ms 7.8 MB
while(step > eps)
{
for(k = 0; k < 4; ++k)
{
nx = x0 + dir[k][0]*step;
ny = y0 + dir[k][1]*step;
d = calSumDis(nx, ny, positions);
if(d < dis)
{
dis = d;
x0 = nx;
y0 = ny;
}
}
step *= 0.95;//或者直接每次都慢慢降低步长
}
60 ms 8.1 MB
我的CSDN博客地址 https://michael.blog.csdn.net/
长按或扫码关注我的公众号(Michael阿明),一起加油、一起学习进步!