LeetCode专项练习之区间合并(Merge Interval)笔记
本文是根据穷码农的LeetCode刷题建议而进行专项练习时记录的心得。
最近弄了一些爬虫,巩固了一下Selenium框架(为此写了一篇CSDN博客),也学习了Pyppeteer,总的来说还是挺有趣的,爬取了一些平常无法下载的网站/文件,并秒杀了口罩(虽然最后口罩已经供大于求了),哈哈哈哈。
言归正传,合并区间在我看来算是比较简单的。解决此类问题可以用相似的思路去套,有一个相对比较系统的方法去应对。
今天的笔记包含区间合并(Merge Interval)类型下的4个题目,它们在leetcode上的编号和题名分别是:
- 56 - Merge Intervals
- 57 - Insert Interval
- 435 - Non-overlapping Intervals
- 986 - Interval List Intersections
下面将根据以上顺序分别记录代码和对应心得,使用的编译器为Pycharm (python3)。
Merge Intervals
Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].
Example 2:
Input: [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.对于区间合并,我们优先需要做的就是排序。然后,通过双指针从左往右滑动,分情况判断是否需要合并区间。需要注意的是此题的边界条件:除非是两区间毫不相交,否则直到右指针走到尾之前都不能添加左指针指向的区间(随时可能会被合并)
class MergeSolution:
def merge(self, intervals: list) -> list:
# special considerations
if len(intervals) == 0 or len(intervals) == 1:
return intervals
# parameters
start, scan = 0, 1
ans = []
# sort the list first
intervalsSorted = sorted(intervals, key=(lambda x: x[0]))
# process it case by case
while scan < len(intervalsSorted):
# [1, 5] and [x, y]
if intervalsSorted[start][1] >= intervalsSorted[scan][0]:
# [1, 5] and [3, y]
if intervalsSorted[start][1] >= intervalsSorted[scan][1]:
if intervalsSorted[start] not in ans and scan == len(intervals)-1:
ans.append(intervalsSorted[start])
else:
# combine [start][0] and [scan][1] by replacing corresponding content
intervalsSorted[scan] = [intervalsSorted[start][0], intervalsSorted[scan][1]]
start = scan
if scan == len(intervals) - 1:
ans.append(intervalsSorted[start])
break
scan += 1
continue
else:
if intervalsSorted[start] not in ans:
ans.append(intervalsSorted[start])
if scan == len(intervals) - 1:
ans.append(intervalsSorted[scan])
break
start = scan
scan += 1
return ansInsert Interval
Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).
You may assume that the intervals were initially sorted according to their start times.
Example 1:
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]
Example 2:
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].基于上一道题的思考,我原本以为通过分情况讨论(if else if else...)就可以解决,但做了一个多小时发现BUG层出不穷,太多情况需要考虑了。在挣扎了一个多小时后我决定放弃这种思路。后来,我突然发现我完全可以利用Merge Interval的思路,把新的区间插入进去,然后合并就行了(自己太傻第一眼都没察觉到代码可以重复利用)。当然,毕竟是练题,所以这种做法也不太好。
最后,在网友提供的思路上,我发现“见缝插针”这个想法很有趣。先新建一个空列表。然后不断往里面填元素。先从原区间列表开始,把里面的区间一个一个塞入空列表,直到区间和插入区间有重合为止。此时再判断插入区间重合到什么程度。
此题特别考察细节,尤其是判断何时开始重合(插入区间左边界是否大于当前列表的右边界),何时结束重合(插入区间的右边界是否大于当前列表的左边界),以及确定边界后什何时添加到新列表里(循环结束后)。注意:判断重合时是一起判断,不要拆分到不同代码块中去判断。
class Solution:
def insert(self, intervals: list, newInterval: list) -> list:
# sepcial considerations:
if len(intervals) == 0 or len(newInterval) == 0:
intervals.append(newInterval)
return intervals
startEle = newInterval[0]
endEle = newInterval[1]
scan = 0
ans = []
# figure out where there is an intersection by comparing the startEle and the right element of current list
while scan < len(intervals) and intervals[scan][1] < startEle:
ans.append(intervals[scan])
scan += 1
# figure out the intersection area
while scan < len(intervals) and intervals[scan][0] <= endEle:
startEle = min(intervals[scan][0], startEle) # 注:将左边界的划分放在这里确定,我之前从未想到。
endEle = max(intervals[scan][1], endEle)
scan += 1
# essential (about the location of this code)
ans.append([startEle, endEle])
# append the remaining elements
while scan < len(intervals):
ans.append(intervals[scan])
scan += 1
return ansNon-overlapping Intervals
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Example 1:
Input: [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.
Example 2:
Input: [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.
Example 3:
Input: [[1,2],[2,3]]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
Note:
You may assume the interval's end point is always bigger than its start point.
Intervals like [1,2] and [2,3] have borders "touching" but they don't overlap each other.此题我一开始也琢磨着分情况讨论,但最后发现使用贪心算法最为合适。贪心算法,就是在每一步选出局部最优解,使得最终结果也为最优解。但这仅适用于一部分情况,并不能应用于所有问题。另外,每一步如何定义"最优解",也是值得考虑的事情。
在此题里,"最优解"的定义就是找到右边界最小的区间,通过循环记录所有与此区间相重叠的区间的个数。若遇到了左边界大于此右边界的区间,则将之替换为新的比较区间,继续循环。
class Solution:
def eraseOverlapIntervals(self, intervals: list) -> int:
intervalLen = len(intervals)
# special considerations:
if intervalLen == 0 or intervalLen == 1:
return 0
# parameters
scan, count = 1, 0
# sort the list to find the interval with smallest right boundary
intervals = sorted(intervals, key=(lambda x: x[1]))
# traverse to filter the overlapping intervals
sebInterval = intervals[0]
while scan < len(intervals):
# essential: if the left boundary of current interval is smaller than our right boundary, they will have
# intersections. Additionally, if not, then this interval will be our new interval with the smallest right
# boundary
if intervals[scan][0] < sebInterval[1]:
count += 1
#intervals.remove(intervals[scan])
else:
sebInterval = intervals[scan]
scan += 1
return countInterval List Intersections
Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
(Formally, a closed interval[a, b](witha <= b) denotes the set of real numbersxwitha <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)
Example 1:
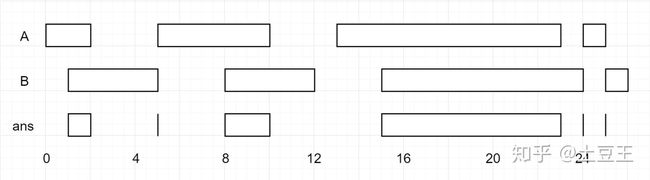
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Reminder: The inputs and the desired output are lists of Interval objects,
and not arrays or lists.
Note:
0 <= A.length < 1000
0 <= B.length < 1000
0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9此题采用双指针(针对A和B),循环遍历即可。每次将指针对应的两个区间分别比较,求出它们的相交区间(如果没有,结果肯定为左区间大于右区间)。之后,我们得理清思路,如果求出了相交区间,我们应该移动哪个指针(看彼此的右区间谁更小)。
class Solution:
def intervalIntersection(self, A: list, B: list) -> list:
# solution: 双指针。分情况判断两个指针指向的块是否有交集,并移动相应指针。
len_A, len_B = len(A), len(B)
# special considerations
if len_A == 0 or len_B == 0:
return None
# parameters (现在针对变量和函数/方法采用"全小写+下划线"式命名,类采用驼峰式命名)
pointer_A, pointer_B = 0, 0
ans = []
while pointer_A < len_A and pointer_B < len_B:
# # 无相交时移动指针 (可优化)
# if A[pointer_A][0] > B[pointer_B][1]:
# pointer_B += 1
# continue
# if A[pointer_A][1] < B[pointer_B][0]:
# pointer_A += 1
# continue
# 优化版本:直接求两区间的相交区间,若求出来左边界比右边界大,便可诠释以上代码
left_boundary = max(A[pointer_A][0], B[pointer_B][0])
right_boundary = min(A[pointer_A][1], B[pointer_B][1])
if left_boundary <= right_boundary:
# 添加相交部分
ans.append([left_boundary, right_boundary])
# 相交时移动指针
if A[pointer_A][1] < B[pointer_B][1]:
pointer_A += 1
else:
pointer_B += 1
return ans总结
至此,区间合并暂告一段落了。它的特点十分显著,在我看来比较容易去分辨,规律也相对明显。
- 题目叙述里,能看出是块与块(区间与区间)的操作。
- 优先进行排序处理。
如果笔记存在一些问题,发现后我会尽快纠正。
*注:本文的所有题目均来源于leetcode