插入、冒泡、归并、选择、快速排序算法以及二分、三分查找算法
六种排序与两种查找算法
一 排序算法 (此处的排序均为升序排列)
排序算法总的来说可以分成内部排序和外部排序 (内外是相对内存而言的,对于内部排序算法,它需要将数据全部加载入内存,才可以进行排序,而外部排序可以将数据分批加载进入内存,进行排序,比如:归并排序);
此外排序算法还可以分为稳定排序和非稳定排序 (若之前A(i) == A(j) && i < j,那么在排序之后A(i)依旧在A(j)的前面,此时我们称该排序算法是稳定的)。
稳定排序有:插入排序,冒泡排序,归并排序
非稳定排序有:选择排序,快速排序, 堆排序, 希尔排序
稳定排序
1. 插入排序

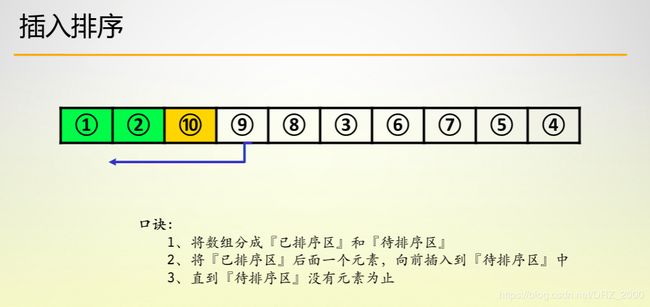
正如口诀所说的那样,我们将数组分为已排序和未排序两部分,我们要做的就是把已排序区域后面的一个元素插入到前面已排序区域的恰当位置,这样直到数组有序,算法结束
对应的实现代码为:
void insert_sort(int *arr, int n) {
for (int i = 1; i < n; i++) {
for (int j = i; j > 0 && arr[j - 1] > arr[j]; j--) {
swap(arr[j], arr[j - 1]);
}
}
}
2. 冒泡排序


冒泡排序同样是将数组分成已排序和未排序两部分,其中已排序的部分是在数组的后方 (注意区分这和插入和选择排序是不同的),我们要做的就是在前面没有排序的部分中,找到最大的一个元素 (通过不断的交换实现),并将该元素放在已排序部分的前面,如此循环,直至未排序部分的元素个数为0,此时算法结束
对应的代码为:
void bubble_sort(int *arr, int n) {
for (int i = 1; i < n; i++) {
int flag = 0;
for (int j = 0; j < n - i; j++) {
if (arr[j] <= arr[j + 1]) continue;
swap(arr[j], arr[j + 1]);
flag = 1;
}
if (!flag) break;
}
}
此时需要注意的是:存在这样的一种情况,在内部循环中并没有进行交换,也就是说,此时数组已经有序,不需要再排序,直接退出即可,为此我们引入标记位flag,当存在交换时flag = 1,若一次内部循环之后,flag没有改变,此时直接跳出循环,算法结束。
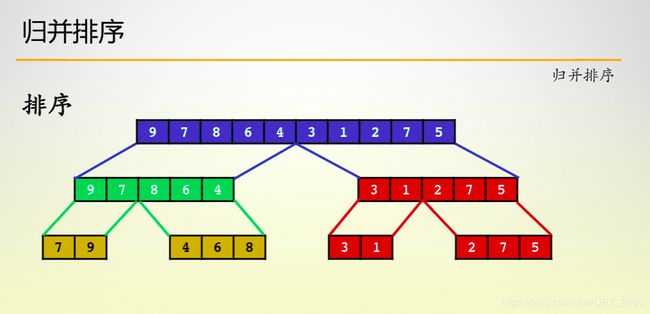
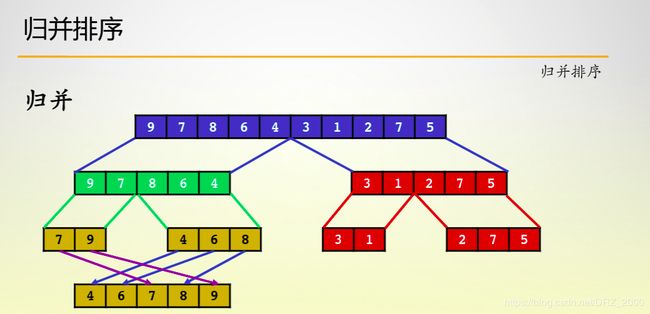
3. 归并排序
归并排序是目前自己知晓的最快的稳定排序,并且重要的是它的时间复杂度稳定在O(N * log N),归并排序充分的利用了分治的思想,将原来的数组对半划分,并分别对这两个子数组进行排序,如此不断的递归下去,当子数组的只有一个或两个元素的时候,此时我们可以处理 (这也是递归的出口),之后我们将数组之间两两之间合并 (只需要两个指针就可实现),这样我们就可以使整个数组有序了。
我们将数组划分为两个子数组,但其实这只是一种,我们称之为2路归并,除此之外,我们还有多路归并,只不过这样排序后合并数组就会比之前麻烦
归并排序还有一个重要的性质:那就是可以实现外部排序,这个算法本身实现的过程有关,比如对于一个32G的数据文件,显然我们不可以全部加载进内存,因此我们可以分8次,每次载入4G的数据进行排序,之后我们得到8个部分有序的子数组,剩下的就是不断地读取数组,将他们合并到一块(我们可以将两个排好序的4G的数据文件,各读取一部分进入内存,边合并边将数据不断的写到外存里面)
void merge_sort(int *arr, int head, int tail) {
if (tail - head <= 1) {
if (tail - head == 1 && arr[head] > arr[tail]) {
swap(arr[head], arr[tail]);
}
return ;
}
int mid = (head + tail) >> 1;
merge_sort(arr, head, mid);
merge_sort(arr, mid + 1, tail);
int *num = (int *)malloc(sizeof(int) * (tail - head + 1));
int p1 = head, p2 = mid + 1, ind = 0;
while (p1 <= mid || p2 <= tail) {
if (p2 > tail || (p1 <= mid && arr[p1] <= arr[p2])) {
num[ind++] = arr[p1++];
} else {
num[ind++] = arr[p2++];
}
}
memcpy(arr + l, num, sizeof(int) * (tail - head + 1));
free(num);
}
其中对于两个子数组的合并,感觉判断条件之间存在交叉和部分独立,但是不影响最后的结果
不稳定排序
1. 选择排序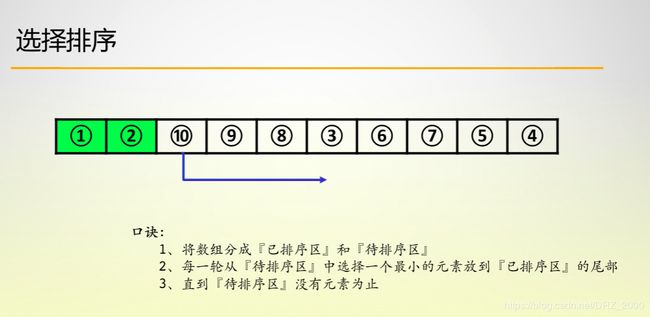
选择排序将数组分为已排序和未排序两部分,我们要做的就是在后面未排序的数组中找到最小的一个元素,将他放在已排序部分的后面,如此循环,直到未排序部分元素的个数为0,算法结束。
实现代码如下:
void select_sort(int *arr, int n) {
for (int i = 0; i < n - 1; i++) {
int ind = i;
for (int j = i; j < n; j++) {
if (arr[i] < arr[ind]) ind = i;
}
if (ind == i) continue;
swap(arr[ind], arr[i]);
}
}
2. 快速排序
快排算法的基本思路就是选取基本元素,并根据首尾两个指针将数组分成两部分,其中前面部分数据均小于基准元素,后面部分均大于基准元素,之后继续对划分后的两个子数组进行划分即可。
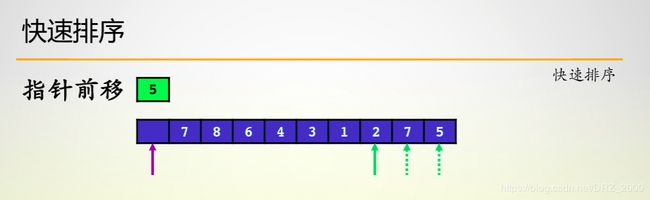
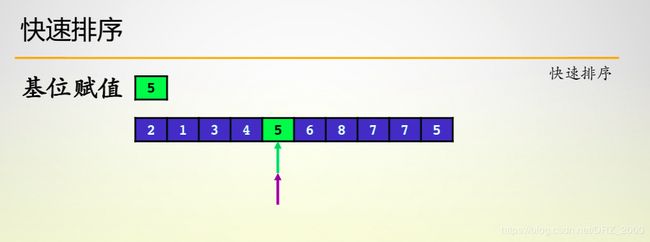
注意:首先前移的一定是尾指针,之后再首尾指针相互移动
对应代码为:
void quick_sort(int *arr, int l, int r) {
if (l > r) return ;
int head = l, tail = r, tmp = arr[head];
while (head != tail) {
while (head < tail && arr[tail] >= tmp) tail--;
while (head < tail && arr[head] <= tmp) head++;
if (tail != head) {
swap(arr[head], arr[tail]);
}
}
arr[l] = arr[head];
arr[head] = tmp;
quick_sort(arr, l, head - 1);
quick_sort(arr, head + 1, r);
}
快排算法的时间复杂性虽然为(n * log n),但是他并不稳定,当数组是逆序排列时,此时会退化成冒泡排序时间复杂度变为O(n * n),所以基准值的选取十分重要,这回直接影响算法的效率,为此,我们可以优化为随机化快排,也就是将最坏事件转换为概率事件,我们在数组中随即选择数字作为划分基准,所以,算法的一般时间复杂性依旧为O(n * log n);
二 查找算法
1. 二分查找
之前最普通的查找算法就是在一个有序的数组中,找到待查找数字的下标,若找不到则返回-1
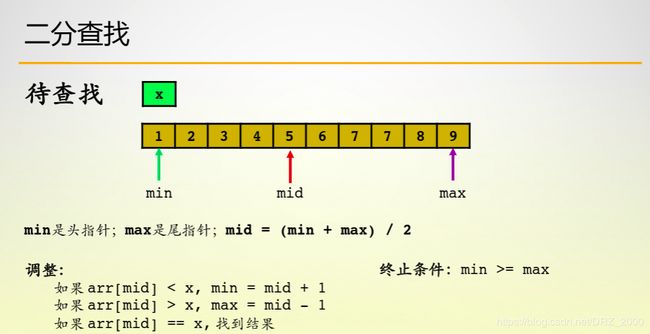
对应代码如下:
void binarySearch(int *arr, int n, int x) {
int head = 0, tail = n - 1, mid;
while (head <= tail) {
mid = (head + tail) >> 1;
if (arr[mid] == x) return mid;
else if (arr[mid] < head) head = mid + 1;
else tail = mid - 1;
}
return -1
}
此外,二分查找还有两种特殊的情况,如下:
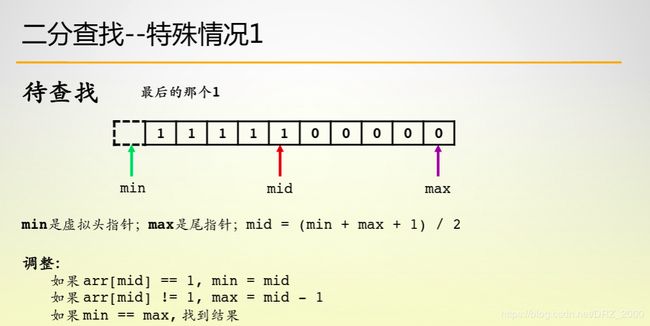
在如1111110000000的数组中,找到最后一个1,首先我们了解max和min是如何变化的,之后我们来考虑一种情况:那就是当这是一个全0的序列,程序结束后min和max均会指向下标为0的元素,所以程序最后的返回将会是0,但这显然是错误的,为了解决这个问题,我们引入了一个虚拟头指针,一开始min指向 -1,现在我们来解释为什么mid = (min + max + 1) >> 2,而不是mid = (min + max) >> 1,因为存在这样一种情况,当最后min和max指向相邻的两个元素时,此时求mid之后,会陷入死循环中,程序无法跳出循环。最后需要注意的是:函数最后返回的是head的值,也就是最后一个1所在的下标,此外有实际出发推演,while循环的条件是min < max没有等号。

第二种特殊情况,这里就不再多说,相似理解,我们直接上代码
void binarySearch_2(int *arr, int n) { //找到最后一个1所在的下标
int head = -1, tail = n - 1, mid;
while (head < tail) {
mid = (head + tail + 1) >> 1;
if (arr[mid] == 1) head = mid;
else tail = mid - 1;
}
return head;
}
void binarySearch_3(int *arr, int n) { //找到第一个1所在的下标
int head = 1, tail = n, mid;
while (head < tail) {
mid = (head + tail) >> 1;
if (arr[mid] == 1) tail = mid;
else head = mid + 1;
}
return head == n ? -1 : head;
}
扩大来说,这里的1并不仅仅是1,其实更多指的是一种性质,我们要找的是找到第一个或者是最后一个满足这种性质的元素下标,这样我们可以避免使用低效的线性搜索,可以使用更高效的二分查找。
- 三分查找
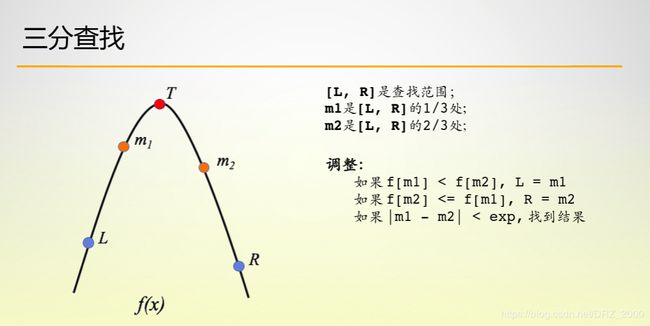
三分查找这里我们用来求的是二次函数极值点的问题,当然对于这个问题我们还可以用求导,使用牛顿迭代法进行求解
三 总代码献上
稳定排序
#include 非稳定排序
#include 二分查找
#include