从晶体管开始聊聊计算机为什么采用二进制

目录

1.理论先行

1.1.二进制思想的提出

1.2.二进制思想的初步实现

1.3.二进制思想在现代计算机上的实现

1.4.二进制运算的好处

2.从晶体管到“1+1=2”

2.1.晶体管如何表示0和1

2.2.从晶体管到门电路

2.3.从门电路到半加器

3.完成一次真正的计算

3.1.穿孔纸带

3.2.演练一番

3.3.编程语言的本质

---

1.理论先行

1.1.二进制思想的提出

二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统，数据在计算机中主要是以补码的形式存储的。

1.2.二进制思想的初步实现

（1）二进制与逻辑代数
1854年，英国数学家乔治•布尔(George Boole)发表了一篇具有里程碑意义的论文，详细描述了一种逻辑代数系统，该系统将被称为布尔代数。他的逻辑推理是在数字电子电路的设计中起了重要的作用。
（2）继电器开关实现二进制的设想
1937年，克劳德•香农(Claude Shannon)在麻省理工学院发表了他的硕士论文，在历史上第一次使用电子继电器和开关实现了布尔代数和二进制算术。香农的论文题目是对继电器和开关电路的符号分析，基本建立了实用的数字电路设计。
（3）继电器计算机
1937年11月，在贝尔实验室工作的乔治•斯提比茨(George Stibitz)完成了一种基于继电器的计算机，他将其命名为“K型”（在他组装的“厨房”中），用二进制加法计算。

1.3.二进制思想在现代计算机上的实现

（1）第一台电脑
1946年诞生了第一台现代电子计算机ENIAC，ENIAC程序和计算是分开的，也就意味着你需要手动输入程序。这种程序的输入需要借助手工插接线的方式进行的，没有存储器且它用布线接板进行控制，运算速度可想而知。而且ENIAC使用的是十进制计算，并不是二进制。
这个时候一位美籍匈牙利数学家——冯•诺伊曼，登场了。
（2）冯•诺依曼的设想
1945年，冯•诺依曼和他的研制小组在共同讨论的基础上发表了一个全新的“存储程序通用电子计算机方案”——EDVAC（Electronic Discrete Variable Automatic Computer），这是一份长达101页的总结报告。报告广泛而具体地介绍了制造电子计算机和程序设计的新思想。
EDVAC方案明确奠定了新机器由五个部分组成，包括：运算器、逻辑控制装置、存储器、输入和输出设备，并描述了这五部分的职能和相互关系．报告中，诺伊曼对EDVAC中的两大设计思想作了进一步的论证，为计算机的设计树立了一座里程碑。
设计思想之一是二进制，他根据电子元件双稳工作的特点，建议在电子计算机中采用二进制。报告提到了二进制的优点，并预言，二进制的采用将大大简化机器的逻辑线路。
（3）冯.诺伊曼的实现
1952 年由计算机之父冯.诺伊曼（Von Neumann）设计的电子计算机EDVAC问世。与它的前任ENIAC不同，EDVAC采用二进制，而且是一台冯•诺依曼结构的计算机。冯.诺伊曼的设想在这台计算机上得到了圆满的体现。
EDVAC是第一台现代意义的通用计算机。它由五个基本部分组成：运算器CA；控制器CC；存储器M；输入装置I；输出装置O。这种体系结构一直延续至今，现在使用的计算机，其基本工作原理仍然是存储程序和程序控制，所以现在一般计算机被称为冯诺依曼结构计算机。

1.4.二进制运算的好处

（1）二进制状态实现简单，可以使用元件开关特性；
（2）可靠性、稳定性高，只有两个状态；
（3）运算规则简单，简化设计；
（4）通用性强。

2.从晶体管到“1+1=2”

我们都知道一台计算机的核心就是处理器（CPU），它的职责就是运算，而CPU是一块超大规模的集成电路，所以我们要想弄清楚计算机的运算机制就要明白集成电路是如何具有运算能力的，而集成电路是由大量晶体管等电子元件封装而成的，所以探究计算机的计算能力就可以从晶体管的功能入手。

2.1.晶体管如何表示0和1

从第一台计算机到EDVAC，这些计算机使用的都是电子管和二极管等元件，利用这些元件的开关特性实现二进制的计算。然而电子管元件有许多明显的缺点。例如，在运行时产生的热量太多，可靠性较差，运算速度不快，价格昂贵，体积庞大，这些都使计算机发展受到限制。

于是，晶体管开始被用来作计算机的元件。晶体管利用电讯号来控制自身的开合，而且开关速度可以非常快，实验室中的切换速度可达100GHz以上。使用了晶体管以后，电子线路的结构大大改观，进入了晶体管为代表的第二代电子计算机时代。
1947年贝尔实验室的肖克利等人发明了晶体管，又叫做三极管。下面两图是晶体管的产品照片和电路符号。需要说明的是，晶体管有很多种类型，每种类型又分为N型和P型，下面图中的电路符号就是一个N型晶体管。

 
晶体管电路有导通和截止两种状态，这两种状态就可以作为“二进制”的基础。从模电角度来说晶体管还有放大状态，但是我们此处考虑的是晶体管应用于数字电路，只要求它作为开关电路，即能够导通和截止就可以了。
如上图所示，当b处电压e处电压时，晶体管中c极和e极截止。
这只是一个简化说明，实际上从模电角度分析，导通和截止的要求是两个PN节正向偏置和反向偏置，还要考虑c极电压，但在实际的数字电路中e极电压和c极电压一般恒定，要么由电源提供、要么接地，所以我们可以简单记为“晶体管电路的通断就是由b极电压与恒定的e极电压比较高低决定”。
换句话说，这个三极管的b极电压相对e极为低电平时三极管就会导通，相对e极为高电平时三极管就会截止。
从这里可以看出，晶体管的导通与截止这两种状态对外可以使用b极电压的相对高低来表示，进而说明了我们可以使用高电平或者低电平状态来表示二进制。
也就是说b极是一个输入量（自变量），可以作为变量存储两个数值：高电平或低电平，相应的输出值（因变量）就是电路实际的变化：导通或截止。
就上面这个N型晶体管而言，高电平截止，低电平导通。那么假如此时我们把高电平作为“1”，低电平作为“0”。那么b极输入1，就会导致电路截止，如果这个电路是控制计算机开关机的，那么就会把计算机关闭。这就是机器语言的原理。我们编程语言的本质就是在编写一大堆高低电平信号。那么如何输入1呢？要知道计算机刚诞生时是没有键盘的，这时就要引入“打孔纸带”这一老物件了，这个东西会在下面细说。
回到晶体管上，实际用于计算机和移动设备上的晶体管大多是MOSFET（金属-氧化物半导体场效应晶体管），它也分为N型和P型，NMOS就是指N型MOSFET，PMOS指的是P型MOSFET。注意，MOS中的栅极Gate可以类比为晶体管中的b极，由它的电压来控制整个MOS管的导通和截止状态。

NMOS电路符号如下图：
 
PMOS电路符号如下图：
 
NMOS在栅极高电平的情况下导通，低电平的情况下截止。所以NMOS的高电平表示“1”，低电平表示“0”；PMOS相反，即低电平为“1”，高电平为“0”。
到了这个时候，你应该明白“1”和“0”只是两个电信号，具体来说是两个电压值，这两个电压可以控制电路的通断。

2.2.从晶体管到门电路

一个MOS只有一个栅极，即只有一个输入，而且输出只是简单的电路导通、截止功能，不能输出高低电压信号，即无法表示“1”或“0”，自然无法完成计算任务，此时就要引入门电路了。小提示，电压、电平、电信号在本文中是一回事。
门电路是数字电路中最基本的逻辑单元。它可以使输出信号与输入信号之间产生一定的逻辑关系。
门电路是由若干二极管、晶体管和其它电子元件组成的，用以实现基本逻辑运算和复合逻辑运算的单元电路。这里只介绍最基础的门电路——与门、或门、非门、异或门。
（1）与门
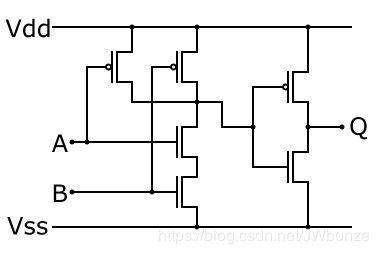
与门电路是指只有在一件事情的所有条件都具备时，事情才会发生。下面是由MOS管组成的电路图。A和B作为输入，Q作为输出。
例如A输入低电平、B输出高电平，那么Q就会输出低电平，转换为二进制就是A输入0、B输出1，那么Q就会输出0，对应的Java语言运算表达式为0&&1=0。
 
（2）或门
或门电路是指只要有一个或一个以上条件满足时，事情就会发生。下面是由MOS管组成的电路图。A和B作为输入，Q作为输出。
例如A输入低电平、B输入高电平，那么Q就会输出高电平，转化为二进制就是A输入0、B输出1，那么Q就会输出1，对应的Java语言运算表达式为0||1=1。

（3）非门
非门电路又叫“否”运算，也称求“反”运算，因此非门电路又称为反相器。下面是由MOS管组成的电路图。非门只有一个输入A，Q作为输出。
例如A输入低电平，那么Q就会输出高电平，转换为二进制就是A输入0，那么Q就会输出1；反之A输入1，Q就会得到0。对应的Java语言运算表达式为！0=1。
 
（4）异或门
异或门电路是判断两个输入是否相同，“异或”代表不同则结果为真。即两个输入电平不同时得到高电平，如果输入电平相同，则得到低电平。
下面是由MOS管组成的电路图。A和B作为输入，Q作为输出。
例如A输入低电平、B输入高电平，那么Q输出高电平，转换为二进制就是A输入0，B输出1，那么Q就会输出1，对应的Java语言运算表达式为0^1=1。

 

2.3.从门电路到半加器

通过门电路，我们可以进行Java语言中逻辑运算了，但是加减乘除等算数运算仍然无法完成，这时需要更复杂的电路单元了。
由基本门电路组成的各种逻辑单元电路登场，假如我们要实现一个最简单的加法运算，计算二进制数1+1 等于几。
我们这时候可以使用半加器实现。
半加器和全加器是算术运算电路中的基本单元，它们是完成1位二进制相加的一种组合逻辑电路，这里的1位就是我们经常说的“1byte=8bit”里的1bit，即如果我们想完成8位二进制的运算就需要8个全加器 。
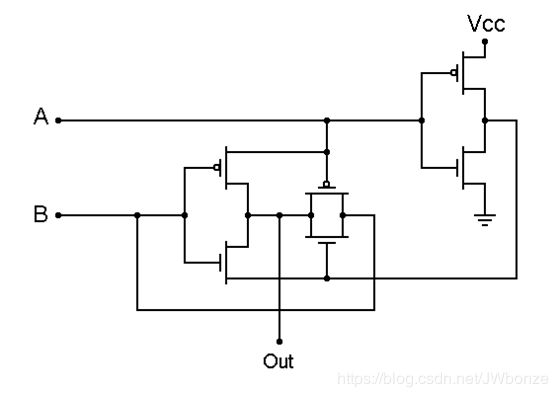
半加器这种加法没有考虑低位来的进位，所以称为半加。下图就是一个半加器电路图。

半加器由与门和异或门电路组成，“=1”所在方框是异或门电路符号，“&”所在方框是与门电路符号。这里面A和B作为输入端，因为没有考虑低位来的进位，所以输入端A和B分别代表两个加数。输出端是S和C0，S是结果，C0是进位。
比如当A=1，B=0的时候，进位C0=0，S=1，即1+0=1。
当A=1，B=1的时候，进位C0=1，S=0，即1+1=10。这个10就是二进制，换成十进制就是用2来表示了，即1+1=2。
到了这里，你应该明白了晶体管怎么计算1+1=2了吧。
然后我们利用这些，再组成全加器。下面是一个全加器电路图，同样只支持1bit计算。Ai和Bi是两个加数，Ci-1是低位进位数，Si是结果，Ci是高位进位数。
 
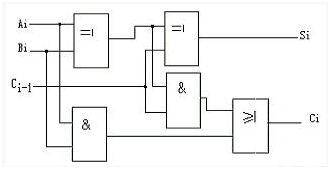
如果我们将4个加法器连接到一起就可以计算4位二进制，比如计算2+3，那么4位二进制就是0010+0011，下表就是利用加法器计算的值。和普通加法一样，从低位开始计算。加数A代表0010，B代表0011。

结果Si：0101，就是十进制5，加法器实现了十进制运算2+3=5。
到这里，本文的核心内容基本说完了。
回忆一下：单一的晶体管只能控制电路通断；多个晶体管组成基本的门电路可以做到输入电信号、输出亦为电信号的基本单元，完成基本逻辑运算；各种门电路组合成一个叫做“加法器”的单元就可以完成加法运算，此时的的这一个单元就是计算机里面说的1bit，如果想计算8位二进制加法，如00010101+01001010就要将8个这样单元电路连接在一起，当然这需要数电方面的知识。
说句题外话，今天我说的主题是计算1+1，加法器使用的是门电路实现的。实际上门电路除了可以构造出做算数的部件之外，还可以构造出具有存储功能的部件和控制电路，比如CPU的构成就是由运算器、控制器和寄存器组组成，寄存器就是由触发器和门电路构成的。有了这些功能部件、存储部件、控制部件，就可以构造出一台简单的计算机模型了。

3.完成一次真正的计算

通过上面的叙述，大家应该明白了01010101这一串数字无非就是高低电平信号，逻辑电路可以把这堆电信号转换成另一堆电信号，那么01010101是怎么来的，这些二进制数字又是如何转换为电信号呢？输出的电信号又以什么方式让人类能够读懂呢？
继续听我唠叨。

3.1.穿孔纸带

穿孔纸带是早期计算机的输入和输出设备，它将程序和数据转换二进制数码：带孔为1，无孔为0，经过光电扫描输入电脑。光电扫描利用光敏电阻感光特性的自然可以做到将数字转换为电信号，比如带孔处透光电阻小，可以得到高电压信号，反之没有孔处低电压信号。
下面这张图是穿孔纸带转化为电信号的一种古老方式，可以让我们更容易理解电脑读取输入的方式。
 
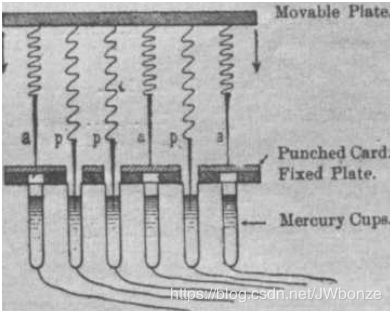
利用电流的通断来识别数据，对应着这个穿孔纸带上的每个数据孔位,上面有着金属针,下面有着容器,容器装着水银。按下压板时，卡片有孔的地方，针可以通过，与水银接触，电路接通，没孔的地方，针就被挡住。
下面是一张穿孔纸带照片，这是我国六七十年代还在使用的输入方式。
 
输入已经理解，输出就不用多说了，输出的高低电压通过机械装置打印出穿孔纸带。不过除此之外，输出的电信号也可以连接其它仪器、电路，比如示波器。

3.2.演练一番

在这里我们清理一下思路：
（1）提出需求：项目中需要计算一下1234567*7654321-987654
（2）十进制转化为二进制，制作穿孔纸带
（3）将穿孔纸带放入计算机，计算机读取数据
（4）计算机一边读取“01”数据，一边将“01”转换为低电压和高电压。
这里说明两点。第一点：低电压和高电压并不是一个具体固定的值。如果计算机输入电压范围为0到10V，以5V作为分界线，那么0~5V内任意电压值都是低电压，5V~10V内任意电压都是高电压。
第二点：进程的引入。计算机运算速度非常快，但是因为需要人为制作穿孔纸带、计算机读取纸带速度也很慢，所以刚开始的时候计算机两次计算之间会留下很长时间，为了不浪费这些计算资源，科学家就引入了“进程”的概念，这样就可以一次性输入多次计算任务，开启计算机后，计算机依次执行相应进程不会有空闲时间。
（5）数据电信号（输入电平）在指令电信号的控制下在电路中进行转换，最后得到一批高低电压（输出电平）。
（6）输出，高低电压信号可以通过打印设备打印出结果。

3.3.编程语言的本质

机器语言就是高低电平不同序列的排列，我们编写的机器语言就是高低电平（0和1）不同序列的排列、不同顺序的输入，经过电脑处理后输出的也是不同序列的高低电平的排列，只是我们通过电路转换，将这些不同序列的高低电平转换成不同旋律音高的声音或明暗色彩不同位置的图像输出，得到我们能够直观理解的信息。
同理，我们的高级编程语言也是这样，只不过人类可读的文本代码需要借助编译器才会生成相应的二进制代码，最后在本机上运行。
一句话，代码就是高低电平的抽象，点击运行后，代码所代表的高低电平组合就会在各种电路中运作了。
最后声明，因为我学的数电模电忘了很多，所以这里面一定会有细节性错误，比如晶体管导通截止条件、没有经过原码补码换算等，但是我这篇博客的目的是理清楚计算机二进制原理实现流程，所以不足之处还请见谅。
【参考资料】
https://baijiahao.baidu.com/s?id=1588291561911438949&wfr=spider&for=pc
http://blog.sina.com.cn/s/blog_6bd3f14f0100lw44.html