数据结构 第五章 树和二叉树 作业
知识点



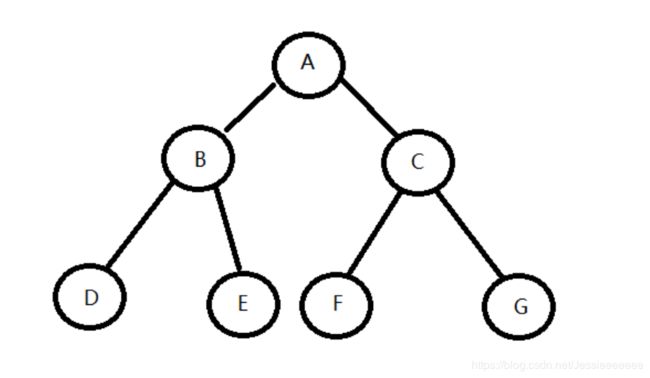
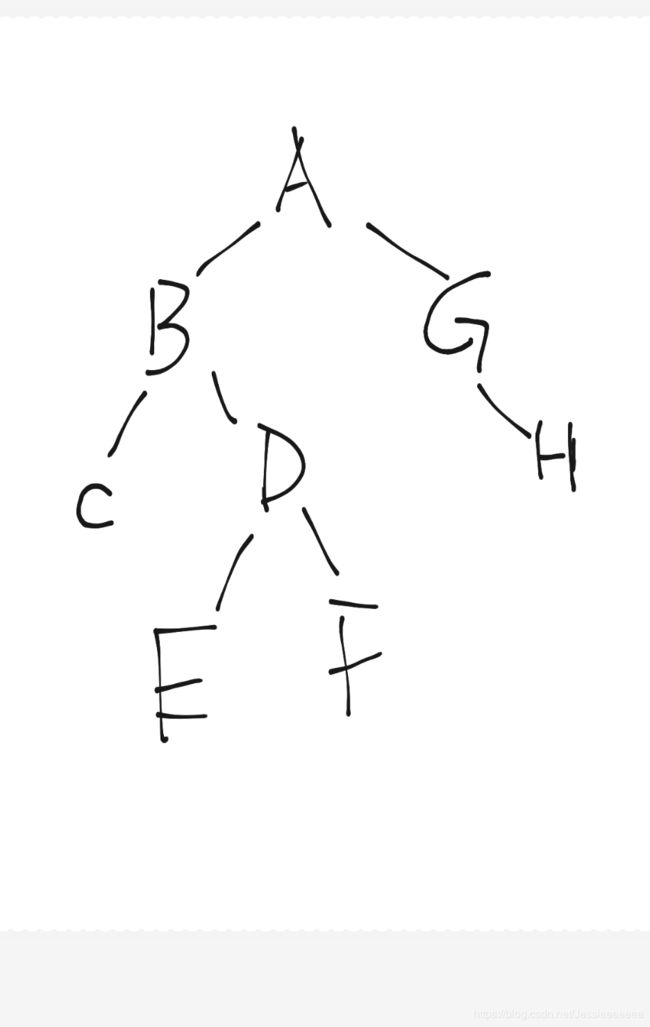
前序遍历:ABDECFG
中序遍历:DBEAFCG
后序遍历:DEBFGCA
层序遍历:ABCDEFG
判断题
1-1
There exists a binary tree with 2016 nodes in total, and with 16 nodes having only one child.
// 存在一棵总共有2016个结点的二叉树,其中有16个结点只有一个孩子
T F
分析: 假设没有孩子的结点(叶结点)个数为n₀,只有一个孩子的结点(度为1的结点)个数为n₁,有两个孩子的结点(度为2的结点)个数为n₂。
则n₀+n₁+n₂=2016 ∵n₀=n₂+1(二叉树的性质:叶结点个数等于度为2的结点个数加1) ∴n₀+n₁+n₂=2016
⇨n₂+1+16+n₂=2016 ⇨2n₂=1999 n₂除不尽,所以答案错误。
1-2
存在一棵总共有2016个结点的二叉树,其中有16个结点只有一个孩子。
T F
1-3
某二叉树的前序和中序遍历序列正好一样,则该二叉树中的任何结点一定都无右孩子。
T F
应是任一结点无左孩子
1-4
一棵有124个结点的完全二叉树,其叶结点个数是确定的。
T F
分析: 假设没有孩子的结点(叶结点)个数为n₀,只有一个孩子的结点(度为1的结点)个数为n₁,有两个孩子的结点(度为2的结点)个数为n₂。
则 n₀+n₁+n₂=124 ∵n₀=n₂+1(二叉树的性质:叶结点个数等于度为2的结点个数加1) ∴n₀+n₁+n₂=124
⇨n₂+1+n₁+n₂=124 ⇨n₁=0 或 n₁=1,所以答案错误。
1-5
若一个结点是某二叉树的中序遍历序列的最后一个结点,则它必是该树的前序遍历序列中的最后一个结点。
T F
单选题
2-1
树最适合于用来表示
A. 有序数据元素
B. 无序数据元素
C. 元素之间无联系的数据
D. 元素之间具有分支层次关系的数据
2-2
设树T的度为4,其中度为1、2、3、4的结点个数分别为4、2、1、1。则T中有多少个叶子结点?
A. 4
B. 6
C. 8
D. 10
度为1,2,3,4的结点个数分别为4,2,1,1
,意思就是有只有一个分支的结点有4个,有两个分支的结点有2个,…结点的度:结点拥有的子树数.(每个结点有多少个分支)
叶子(终端结点):度为零的结点.(没有分支的结点) 树的度:树内各结点的度的最大值.由树的性质知:结点数为所有结点的度数之和加1
,同时注意到叶子结点的度数为0 则总结点数(设叶子结点数为X)
1 * 4+2 * 2+3 * 1+4 * 1+X * 0 + 1 = 16 叶子结点数为
X=16-4-2-1-1=8
2-3
三叉树中,度为1的结点有5个,度为2的结点3个,度为3的结点2个,问该树含有几个叶结点?
A. 8
B. 10
C. 12
D. 13
总结点数:1 * 5 + 2 * 3 + 3 * 2 + X * 0 + 1 = 18
叶子结点数:X = 18 - 5 - 3 - 2 = 8
2-4
有一个四叉树,度2的结点数为2,度3的结点数为3,度4的结点数为4。问该树的叶结点个数是多少?
A. 10
B. 12
C. 20
D. 21
总结点数:1 * 0 + 2 * 2 + 3 * 3 + 4 * 4 + X * 0 + 1 = 30
叶子结点数:X = 30 - 2 - 3 - 4 = 21
2-5
一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为()个。
A. 15
B. 16
C. 17
D. 47
总结点数:1 * 30 + 2 * 15 + X * 0 + 1 = 61
叶子结点数:X = 61 - 30 - 15 = 16
2-6
在一棵度为 3 的树中,度为 2 的结点个数是 1,度为 0 的结点个数是 6,则度为 3 的结点个数是 __
A. 2
B. 3
C. 4
总结点数:1 * 0 + 2 * 1 + 3 * X + 0 * 6 + 1 = 3 + 3 * X
叶子结点数:6 = 3 + 3 * X - 1 - X = 2 + 2 * X
X = 2
2-7
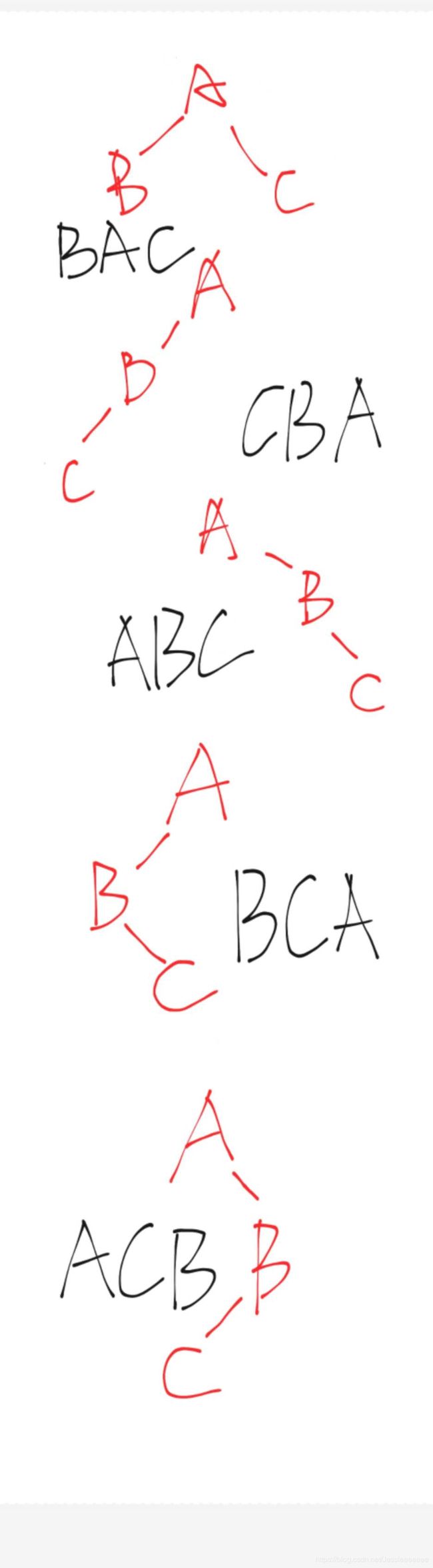
已知一棵二叉树的先序遍历结果是ABC,则以下哪个序列是不可能的中序遍历结果:
2-8
已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则该完全二叉树的结点个数最多是:
A. 39
B. 52
C. 111
D. 119
该完全二叉树第6层的非叶子结点有 2^(6-1) - 8 = 24,
那么第7层最多有 24 * 2 = 48 个结点
而前6层最多有 2^6 - 1 = 63 个结点
所以该完全二叉树的结点个数最多有 63 + 48 = 111 个
2-9
在一个用数组表示的完全二叉树中,如果根结点下标为1,那么下标为17和19这两个结点的最近公共祖先结点在哪里(数组下标)? (注:两个结点的“公共祖先结点”是指同时都是这两个结点祖先的结点)
A. 8
B. 4
C. 2
D. 1
2-10
具有65个结点的完全二叉树其深度为(根的深度为1):
A. 8
B. 7
C. 6
D. 5
因为2^6-1< 65 < 2^7-1
所以是6+1=7
2-11
具有1102个结点的完全二叉树一定有__个叶子结点。
A. 79
B. 551
C. 1063
D. 不确定
设n2为度为2的节点,设n1为度为1的节点,n0为度为0的节点;
叶结点个数等于度为2的结点个数加1,n0=n2+1
n0+n1+n2=1102=n
n = 2 * n2 + 1 + n1
完全二叉树度为知1的节点只能有0个或1个
所以n1=0或者1,用n=2*n2+n1+1;算一下,n2肯定是整数,把0舍去;
求出n2=550;
度为0的节点数等于度为2的节点数+1;
所以叶子节点数为551
2-12
已知二叉树的先序遍历序列为ABCDEFGH,中序遍历序列为CBEDFAGH,则该二叉树形态中,父节点的右子节点为()。
编程填空题
5-1 下列代码的功能是将二叉树T中的结点按照层序遍历的顺序输出。
typedef struct TreeNode *Tree;
struct TreeNode
{
int Key;
Tree Left;
Tree Right;
};
void Level_order ( Tree T )
{
Queue Q;
if ( !T ) return;
Q = CreateQueue( MaxElements );
Enqueue( T, Q ); //入队操作
while ( !IsEmpty( Q ) ){
T = Front_Dequeue ( Q ); /* return the front element and delete it from Q */
printf("%d ", T->Key);
if (T->Left)//如果左子树不为空将左节点入队
Enqueue(T->Left,Q);
if (T->Right) //如果右子树不为空将右节点入队
Enqueue(T->Right,Q);
}
}
编程题
7-1 玩转二叉树
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例:
4 6 1 7 5 3 2
#include7-2 树的遍历
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
#include7-3 列出叶结点
对于给定的二叉树,本题要求你按从上到下、从左到右的顺序输出其所有叶节点。
输入格式:
首先第一行给出一个正整数 N(≤10),为树中结点总数。树中的结点从 0 到 N−1 编号。随后 N 行,每行给出一个对应结点左右孩子的编号。如果某个孩子不存在,则在对应位置给出 “-”。编号间以 1 个空格分隔。
输出格式:
在一行中按规定顺序输出叶节点的编号。编号间以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
输出样例:
4 1 5
#include7-4 小字辈
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。
输入格式:
输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。
输出格式:
首先输出最小的辈分(老祖宗的辈分为 1,以下逐级递增)。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔,行首尾不得有多余空格。
输入样例:
9
2 6 5 5 -1 5 6 4 7
输出样例:
4
1 9
#include
using namespace std;
vector<int>v[200005];
int vv[100005];
queue<int>q;
int main(){
int n,x,lzz;//lzz 记录老祖宗
scanf("%d",&n);
if(n==1){
}
for(int i=1; i<=n; i++){
scanf("%d",&x);
if(x==-1)
lzz=i;
else
v[x].push_back(i);
}
if(n==1){
printf("%d\n%d",1,1);
return 0;
}
q.push(lzz);
int bfen=1; //统计辈分
vv[lzz]=1;
while(!q.empty()){
int temp = q.front();
q.pop();
for(int i=0;i<v[temp].size();i++){
vv[v[temp][i]] = vv[temp]+1;//更新每个人的辈分
bfen = max(bfen,vv[v[temp][i]]);//更新(获得)最小辈分的值
q.push(v[temp][i]);//把下一次要遍历的入队
}
}
printf("%d\n",bfen);
int flag = 0;
for(int i=1;i<=n;i++){
if(vv[i]==bfen){
if(!flag){
printf("%d",i);
flag = 1;
}
else
printf(" %d",i);
}
}
}