ICPC Central Europe Regional Contest 2019 D.Deep800080

题目链接

戳此处

解析

注意，此处码头指的是一条直线。。

a straight line passing throughtwo distinct points with coordinates (0, 0)(0,0) and (A, B)(A,B).

我们考虑，在一条直线上，以点$o$为圆心，$r$为半径的一个圆，如何才能将一个点$p$包含?
显然，以$p$为圆心,同样的做一个半径$r$的圆，其与直线的两个交点形成的线段，便是$o$的取值范围。
如图1：

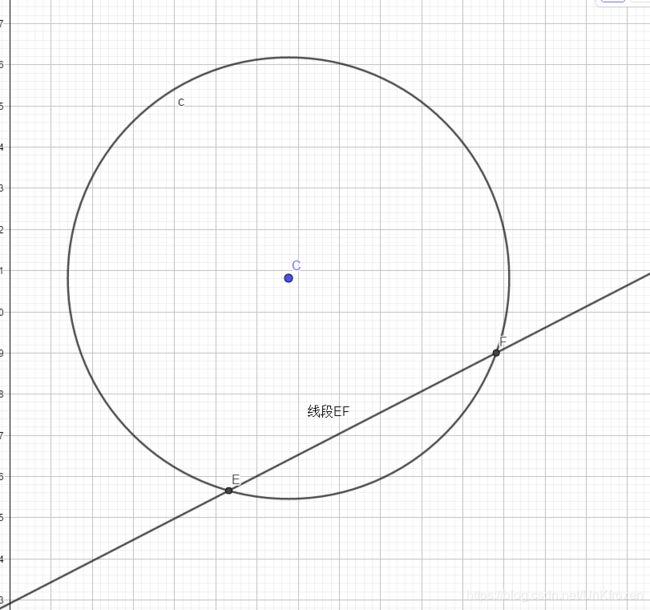
于是乎，题目就从，如何在线上找一点，使得其做的圆包含点最多，变成了线段重叠问题。
问哪个地方线段重叠最多，显然是扫描线类型的题目。
按照一个方向扫过去，碰到一个线段的起点便$ans+=1$，碰到线段的末尾$ans-=1$
如此扫一遍，每次$ans$更改时取一次$maxx$，扫完后的$maxx$便是答案。

代码

/*
#include 
#include 
#include 
#include 
#include 
#include 
*/
#pragma comment(linker, "/STACK:102400000,102400000")
#pragma GCC optimize(3, "Ofast", "inline")
#include 
#include 
using namespace __gnu_pbds;

using namespace std;
#define inf __INT_MAX__
#define enf INT_MIN
#define INF LLONG_MAX
#define ENF LLONG_MIN
const int MAXN = 1e6 + 10;
const double pi = acos(-1.0);
const double eps = 1e-6;
typedef long long ll;
#define zhengfu(x) ((x > eps) - (x < -eps))

typedef struct point vec;
struct point { //点的基本数据结构
    double x, y;
    int poe;
    point(double _x = 0, double _y = 0)
        : x(_x), y(_y) {
    }
    double len() //模长
    {
        return sqrt(x * x + y * y);
    }
    vec chuizhi() {
        return vec(-y, x);
    }
    double operator*(const point &i_T) const //点积
    {
        return x * i_T.x + y * i_T.y;
    }
    double operator^(const point &i_T) const //叉积
    {
        return x * i_T.y - y * i_T.x;
    }
    point operator*(double u) const {
        return point(x * u, y * u);
    }
    bool operator==(const point &i_T) const {
        return fabs(x - i_T.x) < eps && fabs(y - i_T.y) < eps;
    }
    point operator/(double u) const {
        return point(x / u, y / u);
    }
    point operator+(const point &i_T) {
        return point(x + i_T.x, y + i_T.y);
    }
    point operator-(const point &i_T) {
        return point(x - i_T.x, y - i_T.y);
    }
    friend bool operator<(point a, point b) {
        return fabs(a.y - b.y) < eps ? a.x < b.x : a.y < b.y;
    }
    void atn2() {
        poe = atan2(y, x);
    }
    friend ostream &operator<<(ostream &out, point &a) {
        //cout << a.x << ' ' << a.y;
        printf("%.8f %.8f", a.x, a.y);
        return out;
    }
    friend istream &operator>>(istream &in, point &a) {
        scanf("%lf%lf", &a.x, &a.y);
        return in;
    }
};
struct cirles {
    point o;
    double r;
    cirles(point _o = point(), double _r = 0.0)
        : r(_r), o(_o) {
    }
    point Point(double t) //圆上任意一点
    {
        return point(o.x + r * cos(t), o.y + r * sin(t));
    }
    friend istream &operator>>(istream &in, cirles &a) {
        in >> a.o >> a.r;
        return in;
    }
    friend ostream &operator<<(ostream &out, cirles &a) {
        out << a.o << ' ';
        printf("%.8f", a.r);
        return out;
    }
};
typedef struct Line Segment; //线段Segment
struct Line {                //直线
    point a, b;
    double poe;
    Line(point _a = point(), point _b = point())
        : a(_a), b(_b) {
    }
    double len() {
        return (a - b).len();
    }
    friend istream &operator>>(istream &in, Line &a) {
        cin >> a.a >> a.b;
        return in;
    }
    friend ostream &operator<<(ostream &out, Line &a) {
        out << a.a << ' ' << a.b;
        return out;
    }
    bool in(point pi) {
        if (b < a)
            return ((b == pi || b < pi) && (a == pi || pi < a));
        return ((a == pi || a < pi) && (b == pi || pi < b));
    }
    void atn2() {
        poe = atan2(b.y - a.y, b.x - a.x);
    }
};
point zhixian_zhixian_jiaodian(Line l1, Line l2) //两直线交点
{
    double t = ((l1.a.x - l2.a.x) * (l2.a.y - l2.b.y) - (l1.a.y - l2.a.y) * (l2.a.x - l2.b.x)) / ((l1.a.x - l1.b.x) * (l2.a.y - l2.b.y) - (l1.a.y - l1.b.y) * (l2.a.x - l2.b.x));
    return l1.a + (l1.b - l1.a) * t;
}
double zhixian_yuanxin_juli(Line l, cirles a) //直线到圆心的距离
{
    return fabs((a.o - l.a) ^ (l.b - l.a)) / (l.b - l.a).len();
}
int bijiao(double x, double y) {
    if (fabs(x - y) < eps)
        return 0;
    if (x > y)
        return 1;
    return -1;
}
int zhixian_yuan_jiaodian(cirles c, Line l, point &p1, point &p2) { //直线与圆交点以及个数
    if (zhixian_yuanxin_juli(l, c) > c.r)
        return 0;
    point pi = c.o;
    pi.x += l.a.y - l.b.y;
    pi.y += l.b.x - l.a.x;
    pi = zhixian_zhixian_jiaodian(Line(pi, c.o), l);
    double t = sqrt(c.r * c.r - (pi - c.o).len() * (pi - c.o).len()) / (l.a - l.b).len();
    p1 = pi - (l.b - l.a) * t;
    p2 = pi + (l.b - l.a) * t;
    return 1 + !(bijiao(p1.x, p2.x) == 0 && bijiao(p1.y, p2.y) == 0);
}
bool cmp(point a, point b) {
    return (bijiao(a.x, b.x) == 0 ? (bijiao(a.y, b.y) == 0 ? a.poe > b.poe : a.y < b.y) : a.x < b.x);
}
int main() {
    Line l;
    int n, r;
    cin >> n >> r >> l.b;
    vector<cirles> c(n);
    for (auto &p : c) {
        cin >> p.o;
        p.r = r + eps;
    }
    vector<point> p;
    for (auto it : c) {
        point p1, p2;
        if (zhixian_yuan_jiaodian(it, l, p1, p2)) {
            p1.poe = 1;
            p2.poe = -1;
            p.push_back(p1), p.push_back(p2);
        }
    }
    sort(p.begin(), p.end(), cmp);
    ll maxx = 0, sum = 0;
    for (auto it : p) {
        sum += it.poe;
        maxx = max(maxx, abs(sum));
    }
    cout << maxx << endl;
    return 0;
}