不倒嗡嗡
波士顿三一教堂,姜健摄影。
今天(2016年10月4日),诺贝尔评选委员会宣布,将2016年诺贝尔物理学奖授予华盛顿大学的Davdi J. Thouless, 普利斯顿大学的 F. Duncan M. Haldane与布朗大学的J. Micheal Kosterlitz, “因其拓扑相变和拓扑物态的理论发现”。Thouless及其合作者Kosterlitz还发现了固体中能带上的“陈省身示性类”,他们历史上首次把陈类和整数量子霍尔效应直接联系了起来,开创了凝聚态物理体系中的拓扑效应先河,为人类打开了一个未知的世界。
作为陈省身大师的直系后代,老顾和同门师兄师弟们无不激越振奋,再度感喟陈大师的旷世杰作,横亘古今,揭示了自然最为深刻而根本的真理。丘先生曾多次教诲众弟子,“奥妙的自然现象后面必然有优美的数学结构”,“美轮美奂的数学结构必定不是人为的,必然有自然的对应”。当初,卡拉比-丘流形的存在性被丘先生证明之后,数十年间一直被视为是纯粹智力的产物,但是现在早已成为超弦理论的基石。
令老顾觉得妙不可言的是:陈省身示性类在“神圣网格”问题中,也起到了根本的作用。因此,在得知拓扑相变获得诺贝尔奖之后,老顾迫不及待地提笔写下“圣杯问题”系列的第二篇文章 - 陈类的巧妙应用。
四边形网格的可拓展问题
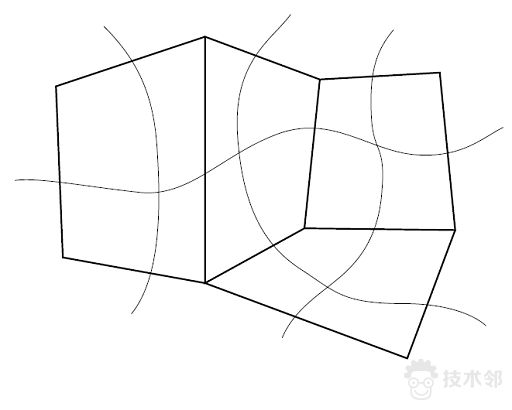
图1. 给定边界曲面
的四边形网格
。
猜测的充分性证明成为关键。Mac Casale为此给菲尔茨奖得主瑟斯顿(Bill Thurston)发去了电子邮件进行询问。瑟斯顿在1993年10月25日给出了公开解答【1】,瑟斯顿的解答简短抽象,但却意蕴深远。瑟斯顿从未正式发表他的想法,但是其思想精髓指导了非结构六面体网格生成领域的发展。在1996年,Scott Mitchell发表了类似思想,并将这一方法推广到复杂拓扑曲面【2】。目前,人们将这一理论统称为Mitchell-Thurston理论。
对偶的观点
瑟斯顿首先只考虑了拓扑六面体剖分,即每个胞腔是拓扑六面体,然后再考虑几何嵌入问题。我们依循他的思路来考察,核心的想法是对偶。
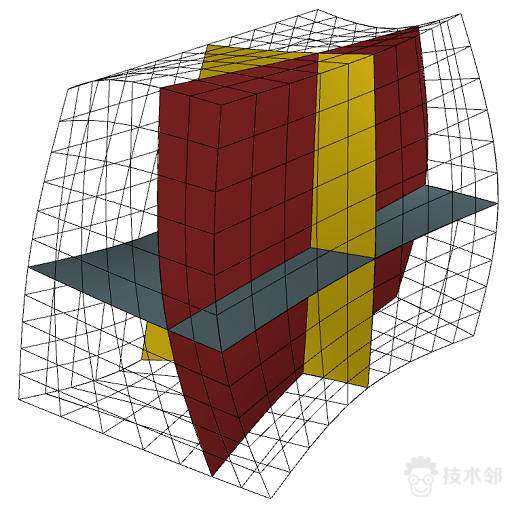
图4. 六面体网格H的对偶H*。
同理,我们介绍实体Ω的六面体网格H的对偶H*。如图4所示,我们在每个六面体中构造三张曲面片,彼此横截相交,共同交于一点。这些曲面片连接,得到全局曲面,这些曲面横截相交,构成对偶的曲面网格H*。H*将体Ω进行胞腔分解,H*的每个顶点都由三张曲面彼此横截相交得来。
六面体网格的对偶H*和边界曲面
的交集就是四边形网格的对偶Q*。瑟斯顿的核心想法是从Q*出发来构建H*。问题的关键在于,我们能否从Q*出发来构建H*,这种构建过程中可能遇到的障碍究竟是什么?
答案在于,光滑曲面的稳定相交情形的拓扑分类。
曲面横截相交理论
在微分拓扑中,惠特尼(Whitney)对三维空间中光滑曲面的稳定相交情形进行了分类【3】。
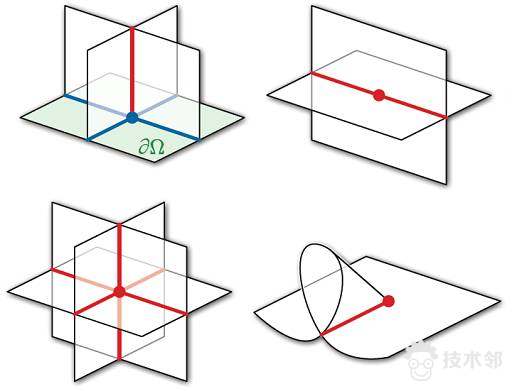
图5. 曲面稳定相交的分类, 边界双重点(boundary double point),内部双重点(interior double point),三重点(triple point),分支点(branch point)。
给定三维空间中的一族浸入曲面,曲面之间的交点被称为奇异点。经过微小扰动,曲面之间彼此不相切,所有奇异点都是稳定奇异点。图5给出了稳定奇异点的分类。我们看到,在六面体对偶网格H*中,前面三种情况都有可能发生,但是最后一种分支奇异点不会发生。因此,在从Q*出发来构建H*的过程中,关键是:确保分支奇异点不会出现!
瑟斯顿把Q*拓展成H*的思路分成两个主要步骤:
在第一步中,我们需要判定边界曲面上两个光滑封闭曲线是否能够光滑地彼此渐变过去,这就是正则同伦的概念。
正则同伦理论
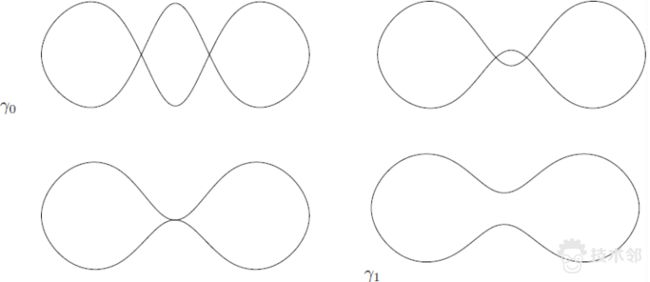
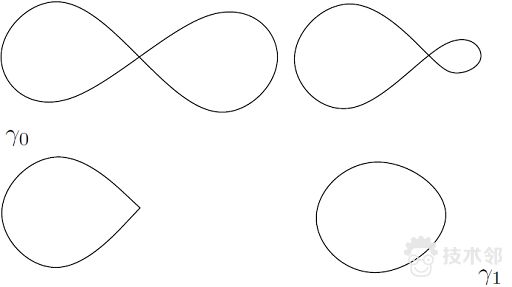
图6. 具有偶数个自相交点的圈和简单圈(无自相交点)正则同伦。
图7. 具有奇数个自相交点的圈和简单圈同伦,但是不正则同伦。
图7显示了具有奇数个自相交点的圈和简单圈同伦,但是并不正则同伦,因为在形变过程中,出现了尖点,在尖点处曲线的切向量无法定义。
陈省身示性类
我们考察球面的单位切丛。首先,根据“法球定理”(hair ball),我们无法将一个椰子上的须毛梳理光顺,总是存在几个奇异点。换言之,球面上的光滑切矢量场,必然存在零点。用我们现在的语言来解释就是:在单位切丛中,我们是否能够找到一张光滑曲面(全局截面),全局截面和所有的纤维只有一个交点。全局截面的存在性障碍就是陈省身示性类。全局截面,就是曲面上处处非零的光滑切矢量场。
图8.球面的单位切丛。
那么,我们如何消除分支奇异点呢?瑟斯顿提出了一个绝妙的主意。
瑟斯顿的手术
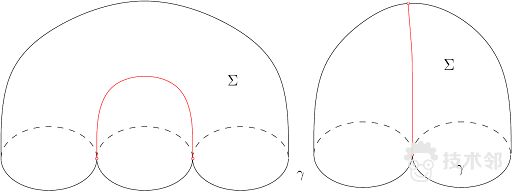
瑟斯顿说给了一对分支奇异点,我们可以如图10所示对曲面进行手术,从而消除分支奇异点。
图10. 瑟斯顿的手术,消除分支奇异点【4】。
气泡包裹法
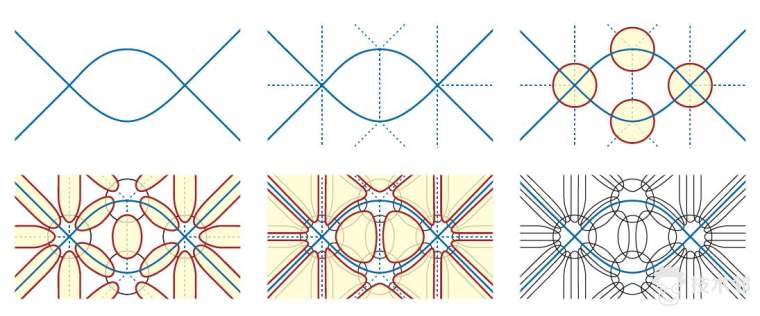
图11. 二维的气泡包裹法(bubble-wrap)【4】。
Mitchell-Thurston 理论
至此,我们已经详细分析了 Mitchell-Thurston理论的所有组成部分,因为逻辑链条过长,我们在这里进行汇总。
小结
我们看到,貌似简单的六面体网格问题涉及了许多拓扑学中的深刻定理和复杂工具,包括惠特尼的子流形稳定横截理论,陈省身的纤维丛示性类理论,斯梅尔的正则同伦理论,瑟斯顿的手术和气泡包裹技巧。
那么,复杂拓扑体的非结构六面体网格存在性理论又是如何呢?我们将会在下篇再用同调理论来详尽解释。