深度模型(十三):Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts
1 简介
近些年深度神经网络被成功地应用于了各种大规模系统中,比如推荐系统[11]。在这些推荐系统中我们经常需要同时优化多个目标。例如,在电影推荐系统中,我们不仅希望用户购买和观看系统推荐的电影,还希望用户能喜欢系统推荐的电影。我们可以建立模型,同时预测用户的购买和评分。实际上,很多大规模的推荐系统已经使用了深度神经网络(DNN)进行多任务学习[3]。
一些研究报告表明通过正则化和迁移学习,多任务学习模型能够提升多个任务的预测能力[8]。但是实际中多任务学习模型并不能总是超越相应的单任务模型[23,26]。实际上很多基于DNN的多任务学习模型对数据分布和多任务之间的关系等因素比较敏感。任务间差异的固有冲突可能会影响一些任务的预测,特别是当任务间广泛的共享参数的时候。
之前的一些研究工作[4,6,8],通过假定每个任务的数据的产生过程来研究任务间的差异,衡量任务间的区别,然后提出一些建议。但是实际应用中,数据模式往往复杂很多,很难量化衡量任务间的差异,前面这些研究提出的建议也很难应用。
最近有一些不依赖显式任务差别衡量的多任务学习方法[15,27,34]被提出。这些方法为了适应任务的差异为每个任务添加了更多的模型参数。因为大规模的推荐系统的模型一般包含百万甚至数十亿的模型参数,增加参数往往受到限制。受限制于有限的服务资源,实际生产环境中计算量的增加往往不可行。
受Mixture-of-Experts(MoE)模型和MoE网络层的启发,本文提出了一种基于Multi-gate Mixture-of-Experts(MMoE)结构的多任务学习方法。MMoE显式地建模任务间的差异,为了利用共享参数针对每个单任务学习相应的函数。通过自动分配的参数捕捉任务共享信息或特定任务信息,避免了为每个任务单独添加新的参数。
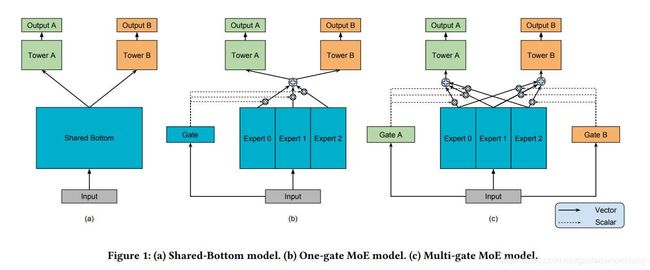
MMoE基于最常见的共享底层网络多任务深度学习结构[8],共享底层结构如图1(a)所示,最底层是输入层,然后是共享网络层,最上层每个单任务都对应一个单独的塔结构。MMoE结构如图1©,有一组底层网络,每一个网络称之为专家。本文中,每一个专家都是一个前向传播网络。然后MMoE为每一个任务引入一个门网络。门网络的输入是特征,输出为专家的权重值,使得不同的任务以不同的方式利用专家网络的输出。一般情况下专家网络输出的加权结果,会作为任务对应的塔网络的输入。通过这种方式,门网络可以学习到专家的不同混合方式,建模任务间的关系。
为了理解MMoE如何针对不同的任务关系学习专家网络和门网络,我们设计一个实验,实验中我们可以通过Pearson相关性量化和控制任务间的关系。类似于[24],我们使用两个回归任务,并且采用正弦函数作为数据产生机制来引入非线性。在这个设定下我们的方法超过了基础方法,尤其是在任务的相关性很低的时候。实验中我们还返现MMoE模型易于训练,收敛速度更快,若干轮训练之后损失值收敛到更低。这个与最近的一些研究发现相关:研究表明调制和门机制可以改善非凸深度神经网络的可训练性[10,19]。
我们进一步在UCI收入普查数据集上评测了MMoE的表现。在多任务学习的设定下,相对于其他几种最先进的多任务学习模型取得了提升。
最后我们在一个实际的大规模推荐系统中测试了MMoE,系统涉及两个分类学习任务。经过数十亿数据的训练之后,相对于普通的共享底层网络,MMoE在离线指标上取得了明显的提升,比如AUC。除此之外,MMoE模型也持续提升了在线指标。
本文的共享有三:首先,我们提出了MMoE模型,显式的建模任务间的关系。通过调制和门机制,我们的模型自动的调整参数,建模任务共享信息和任务特定信息。第二,我们设计在合成数据上的可控实验,发现了任务间的关系如何影响多任务学习训练,以及MMoE如何提升了模型的表达能力和模型的可训练性。最后,我们在测试数据和涉及数亿用户和物品的推荐系统上设计了实验。实验证明了MMoE在实际设定中的有效性。
2 相关工作
2.1 DNN中的多任务学习
多任务模型能学习到多个任务的共同点和不同点,既可以提升模型的效率有可以提升模型的效果。一种广泛被采用的多任务模型结构由Caruana[8,9]提出,拥有一个共享的底层模型结构,被所有任务所共享。这种结构显著的降低了过拟合的风险,但是任务间的差异也会导致优化冲突,因为所有的任务需要共用共享层的参数。
为了理解任务相关性是如何影响模型效果,之前的工作采用合成数据和控制任务相关性的方式来评测多任务模型的效果[4-6,8]。
最近一些其他的方法被提出来,这些方式没有采用共享隐藏层和模型参数的方式,而是给每个特定任务的参数添加不同的约束[15,27,34]。例如,对于两个任务的模型, Duong等[15]在两组参数之间添加了L-2约束。[27]为每一个任务学习了任务特定的隐藏层embedding的唯一组合。Yangd等[34]使用张量分解模型为每个任务产生隐藏层参数。相对于共享底层模型,这些方式包含更多的任务特定参数,在任务差异导致共享参数更新冲突的情况下取得了更好的效果。然后更多的任务特定参数需要更多的训练数据,并且在大规模的模型中可能会有效率问题。
2.2 集成子网络和专家
本文中我们采用了一些深度学习进来的研究成果,例如参数调制和建模多任务关系。在DNN中,模型集成和子网络集成已经被证明是一种有效提升模型效果的方法。
Eigen[16]和Shazeer[31]将混合专家模型改进为基本的网名模块(MoE层),组成其他DNN网络。MoE层基于训练和服务时的输入选择不同的子网络(专家)。因此此模型不仅建模能力更加强大,而且计算量更小。类似,PathNet[17]网络,专门为通用AI任务设计,拥有多层网络,每层网络拥有多个子模块。当训练某个特定任务时,多个路径被随机选择,同时训练。最佳路径上的参数被固定,然后给新的任务选择新的路径。受到这些工作的启发,我们集成多个子网络(专家),实现了迁移学习,并节约了计算量。
2.3 多任务学习的应用
得益于分布式机器学习系统的开发,很多实际中的大规模应用都采用了基于DNN的多任务学习算法,并取得了可观的收益。在多语言翻译任务中,通过参数共享,有限训练数据的翻译任务与大量训练数据的翻译任务共同训练,有效提升了前者的效果[22]。推荐系统中,多任务学习被证明对上下文感知的推荐有帮助[28,35]。[3]中的文本推荐任务,通过共享特征表示和底层隐藏层提升了效果。[11]中的视频推荐采用共享底层模型的方式学习视频的排序算法。与这些工作类似,我们在实际中的大规模推荐系统中评测了我们的模型。我们证明了我们的模型具有可扩展性,并且相对于其他最先进的建模方式取得了效果。
3 准备工作
3.1 共享底层的多任务模型
首先我们介绍一下图1(a)中的共享底层多任务模型,由Rich Caruana[8]提出的结构,广泛的应用于很多任务学习问题[18,29]。因此我们把它作为多任务建模的baseline方法。
给定K个任务,模型包含一个共享的底层网络,表示为函数 f f f,和K个塔网络 h k h^k hk,其中 k = 1 , 2 , . . . , K k=1,2,...,K k=1,2,...,K。对于任务 k k k模型的输出 y k y^k yk可以表示为:
y k = h k ( f ( x ) ) . ( 1 ) y^k=h^k(f(x)). \space\space\space\space (1) yk=hk(f(x)). (1)
3.2 合成数据
研究[15,27]表明多任务学习模型的效果很大程度的依赖于任务间的内在关系。在实际的应用中,我们很难研究任务间的关系是如何影响多任务模型的,因为我们很难改变实际应用中多任务间的关系然后观察结果。因此为了研究这种关系,我们首先需要通过人工合成的方式产生需要的数据,这里我们可以方便的量化和控制任务间的关系。
受Kang等[24]工作的启发,我们合成两个回归任务,使用两个任务标签间Pearson相关性作为衡量任务相关性的指标。因为我们主要关注DNN模型,我们使用正选函数[33]提点线性函数[24]。具体来说,我们采用以下方式合成数据:
(1) 给定输入特征的维度d,我们产生两个正交单位向量 u 1 , u 2 ∈ R d u_1,u_2\in R^d u1,u2∈Rd满足:
u 1 T u 2 = 0 , ∣ ∣ u 1 ∣ ∣ = 1 , ∣ ∣ u 2 ∣ ∣ = 1 u_1^Tu_2=0,||u_1||=1,||u_2||=1 u1Tu2=0,∣∣u1∣∣=1,∣∣u2∣∣=1
(2) 给定常量 c c c和相关性分数$-1 \le p \le 1 , 生 成 两 个 权 重 向 量 ,生成两个权重向量 ,生成两个权重向量w_1, w_2$满足:
w 1 = c u 1 . w 2 = c ( p u 1 + ( 1 − p 2 ) u 2 ) . ( 2 ) w_1=cu_1. w_2=c(pu_1+\sqrt{(1-p^2)}u_2).\space\space\space\space\space\space(2) w1=cu1.w2=c(pu1+(1−p2)u2). (2)
(3) 随机采样输入数据点 x ∈ R d x\in R^d x∈Rd,满足分布 N ( 0 , 1 ) N(0, 1) N(0,1).
(4) 按以下方式产生标签 y 1 , y 2 y_1, y_2 y1,y2:
y 1 = w 1 T x + ∑ i = 1 m s i n ( α i w 1 T x + β i ) + ϵ 1 ( 3 ) y_1=w_1^Tx+\sum_{i=1}^msin(\alpha_iw_1^Tx+\beta_i)+\epsilon_1\space\space\space\space(3) y1=w1Tx+i=1∑msin(αiw1Tx+βi)+ϵ1 (3)
y 2 = w 2 T x + ∑ i = 1 m s i n ( α i w 2 T x + β 2 ) + ϵ 2 ( 4 ) y_2=w_2^Tx+\sum_{i=1}^msin(\alpha_iw_2^Tx+\beta_2)+\epsilon_2\space\space\space\space(4) y2=w2Tx+i=1∑msin(αiw2Tx+β2)+ϵ2 (4)
其中 α i , β i , i = 1 , 2 , . . . , m \alpha_i,\beta_i,i=1,2,...,m αi,βi,i=1,2,...,m为给定参数,控制正选函数的形状, ϵ 1 , ϵ 2 ∼ N ( 0 , 0.001 ) \epsilon_1,\epsilon_2 \sim N(0, 0.001) ϵ1,ϵ2∼N(0,0.001).
(5) 重复(3)和(4),直到数据足够为止。
由于非线性的数据产生过程,不能为给定的标签Pearson相关性直接生成任务。我们操作公式(2)中的权重向量的余弦相似度,也就是 c o s ( w 1 , w 2 ) = p cos(w_1,w_2)=p cos(w1,w2)=p,然后衡量标签的Pearson相关度。需要注意的是,线性情况向下:
y 1 = w 1 T x + ϵ 1 y_1=w_1^Tx+\epsilon_1 y1=w1Tx+ϵ1
y 2 = w 2 T x + ϵ 2 y_2=w_2^Tx+\epsilon_2 y2=w2Tx+ϵ2
标签之家的Pearson相关度等于 p p p.
非线性情况下,公式(3)(4)中的标签 y 1 , y 2 y_1, y_2 y1,y2的相关性如图(2)所示:
3.3 任务相关性的影响
为了验证低相关度对baseline多任务模型效果的负面影响,在合成数据上我们做了以下的实验:
(1)给定若干任务相关性,分别生成多组的数据
(2) 为每一组数据训练一个共享底层的多任务模型,并且保持模型超参不变
(3)重复(1)(2)两步上百次,但保持相关性列表和超参不变
(4)计算每个任务相关性对应的模型效果的平均值
图3显示了不同的任务相关性下损失值曲线。果然如预期一样,随着相关性的降低,模型的效果呈下降趋势。在不同的超参取值下,这种趋势是一致的。图3中只展示了实验结果的一个例子,本例中每个塔网络是单层神经网络,包含8个神经元。共享的底层网络是包含16个神经元的单层网络。模型采用TensorFlow实现,使用默认设置的Adam算法优化。实验结果验证了我们的假设:传统的多任务模型对任务的相关性敏感。
4 模型
4.1 混合专家模型(MoE)
原始的混合专家模型可以表示为:
y = ∑ i = 1 n g ( x ) i f i ( x ) ( 5 ) y=\sum_{i=1}^ng(x)_if_i(x)\space\space\space\space(5) y=i=1∑ng(x)ifi(x) (5)
其中 ∑ i = 1 n g ( x ) i = 1 \sum_{i=1}^ng(x)_i=1 ∑i=1ng(x)i=1, g ( x ) i g(x)_i g(x)i表示专家 f i f_i fi的概率。 f i , i = 1 , 2 , . . . , n f_i, i=1,2,...,n fi,i=1,2,...,n表示n个专家网络, g g g表示集成专家输出的门网络。
4.2 多门混合专家模型(MMoE)
MMoE模型为每一个任务添加一个单独的门网络 g k g^k gk,MMoE模型可以为:
y k = h k ( f k ( x ) ) ( 6 ) y^k=h^k(f^k(x))\space\space\space\space(6) yk=hk(fk(x)) (6)
f k ( x ) = ∑ i = 1 n g k ( x ) i f i ( x ) ( 7 ) f^k(x)=\sum_{i=1}^ng^k(x)_if_i(x)\space\space\space\space(7) fk(x)=i=1∑ngk(x)ifi(x) (7)
g k ( x ) = s o f t m a x ( W g k x ) ( 8 ) g^k(x)=softmax(W_{gk}x)\space\space\space\space(8) gk(x)=softmax(Wgkx) (8)
其中 W g k ∈ R n × d W_{gk}\in R^{n\times d} Wgk∈Rn×d,n表示专家的数量,d表示特定的维度。
每一个门网络可以基于输入样本学习选择专家。在多任务学习中这对于灵活的参数共享来说非常有必要。举一个特例,比如只有一个最高分数的专家被选择,则每一个门网络实际上将输入划分为n个区域,每个区域由一个专家负责。MMoE模型通过相互有所重叠的区域划分方式来建模任务间的关系。如果任务不怎么相关,则共享的专家会收到惩罚,相关的任务则会学习利用不同的专家。相对于共享底层模型,MMoE只额外添加了门网络,参数数量几乎可以忽略不计。因此整个网络还是可以受益于多任务学习中的知识迁移。
为了理解独立的门网络可以帮助模型学习任务特定的知识,我们比较了单一门网络模型,我们称之为OMoE(One-gate Mixture-of-Experts):