再看运放之要点

上个月4月8日写过《关于运放的选型参数》，但只是一些比较浅的东西，没有展开和深入，后面再调电路时，还是不太会用。再深化一下。

基本原理：

如果先后分别从这两个输入端输入同样的信号，则在输出端会得到电压相同但极性相反的输出信号：输出端输出的信号与同相输人端的信号同相，而与反相输入端的信号反相。

运算放大器有一些非常有意思的特性，灵活应用这些特性可以获得很多独特的用途，总的来说，这些特性可以综合为两条：

1、运算放大器的放大倍数为无穷大。（输入端压差放大并且输出端跟随输入端压差变化）

2、运算放大器的输入端电阻为无穷大，没有压差。（得出输入输出公式）。

首先，运算放大器的放大倍数为无穷大，所以只要它的输入端的输入电压不为零，输出端就会有与正的或负的电源一样高的输出电压本来应该是无穷高的输出电压，但受到电源电压的限制。准确地说，如果同相输入端输入的电压比反相输入端输入的电压高，哪怕只高极小的一点，运算放大器的输出端就会输出一个与正电源电压相同的电压;反之，如果反相输入端输入的电压比同相输人端输入的电压高，运算放大器的输出端就会输出一个与负电源电压相同的电压(如果运算放大器用的是单电源，则输出电压为零)。

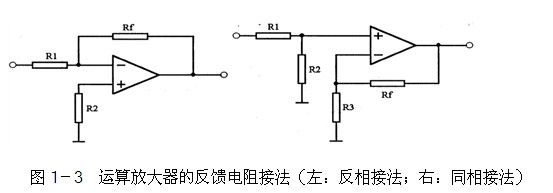
其次，由于放大倍数为无穷大，所以不能将运算放大器直接用来做放大器用，必须要将输出的信号反馈到反相输入端(称为负反馈)来降低它的放大倍数。如图1-3中左图所示，由于反相输入端与输出的电压是相反的，所以会减小电路的放大倍数，是一个负反馈电路，电阻Rf也叫做负反馈电阻。

还有，由于运算放大器的输入为无穷大，所以运算放大器的输入端是没有电流输入的——它只接受电压。同样，如果我们想象在运算放大器的同相输入端与反相输入端之间是一只无穷大的电阻（虚断），那么加在这个电阻两端的电压是不能形成电流的，没有电流，根据欧姆定律，电阻两端就不会有电压差，所以我们又可以认为在运算放大器的两个输人端电压是相同的(电压在这种情况就有点像用导线将两个输入端短路，所以我们又将这种现象叫做“虚短”)。

 

不同反馈接法时输入输出公式：

1、

 根据虚断特性，Vin端趋于0（正相端电压），又因为Vin到Vout电流相同，所以(Vin-0)/Rin=(0-Vout)/Rf,得到

Vout=(- Rf/Rin)Vin.

根据“虚断”的特性 

1）Vin趋近于2脚（反向端）的电压，记为Vp,所以Vin=Vp.
2）流过电阻R2的电流就是流过电阻R1的电流，即I1=I2，因此有

(0-Vp)/R2=(Vp-Vout)/R1   ->    Vout=(R1+R2)*Vp/R2   --->   Vout=(R1+R2)/R2  * Vin

Vout存在的意义就在于使得Vin+与Vin-压差趋近于0，或接近于无穷小。

由“虚断”特性可知 电阻Rf上的电压=Vin+,那么电流=Vin/Rf.

得出IRL=IRf=Vout/(RL+RF)=Vin/Rf

该电路是通过输入Vin控制输出Vout的变化，只要Rf和Vin固定，无论电路参数如何变化，都能获取到恒定电流。

 

还是根据“虚断”特性。Rf端在Vin端电压趋近于0(正反馈端）电压。得出等效图，可知，电流由Rf端输入，则Rf与R1端电流相同，相当于两者都并联到地，所以此时的VRf=VR1  --> 电压相等的话，根据并联电路总的电流等于各分支电流之和，所以I总=IRf+IR1所以V/R总=V/Rf+V/R1,得到R总=（Rf * R1) / (Rf+R1) ，又串联上Rl,所以IRl=IR总=VRf * (Rf+R1)/Rf *R1,消去VRf=I(in)*Rf

IR=I(in)*Rf   * (Rf+R1)/Rf *R1 = I(in)*(Rf+R1)/R1,由此，得到最终

          IRl=I(in) * (1+Rf/R1),可知，流过Rl的电流与Rl无关，只与Rf与R1相关。

何为并联与串联呢？

信号输入与反馈信号加到两个输 入端就是串联，加到同一个输入端就是并联。

何为电压反馈，同样，何为电流反馈呢？

反馈电路直接从Vout端引出就是电压反馈

若从Vout端又接电阻到地，则是电流反馈。

负反馈电路分析方法？

根据运放“虚断”的特点，将运放消掉，将电容、电感等看作是可变电阻（针对不同频率信号电阻不同）分析，最后电路只剩下符合伏安特性的电阻电路方便定性分析。