数据结构 二叉树的基本操作(求树的结点数，高度，叶子结点...)

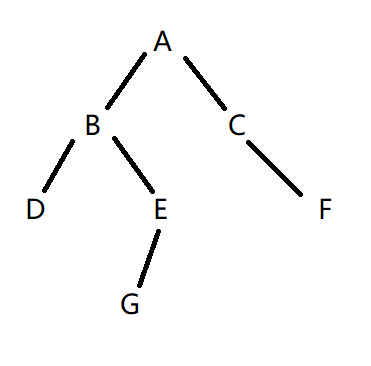
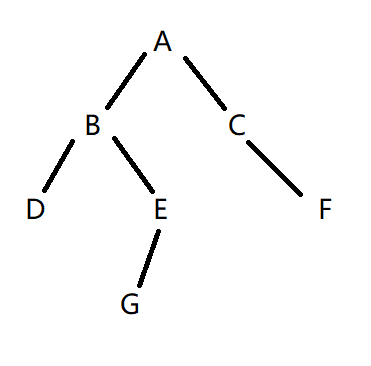
以下代码所测试的树：

根据先序遍历结果(带空结点)，构造一棵树

将树的先序遍历放入数组，空结点用*代替

char arr[] = "abd**eg***c*f**";

再然后，与递归前序遍历树的方法一样，只是将打印该结点换成创建结点即可。

代码实现：

//根据先序遍历结果(带空结点)，构造一棵树
TreeNode* _TreeCreate(TreeDataType arr[],size_t size,int* index,TreeDataType null_node)
{
	if(index == NULL)	
	{
		//非法输入
		return NULL;
	}
	if((*index) >= size)
	{
		//说明数组已遍历完,数组的每个元素都放入二叉树中
		return NULL;
	}
	//判断是否为空结点
	if(arr[*index] == null_node)
	{
		return NULL;
	}
	//创建根结点
	TreeNode* new_node = CreateTreeNode(arr[*index]);

	//递归遍历左子树
	(*index)++;
	new_node->lchild = _TreeCreate(arr,size,index,null_node);
	//递归遍历右子树
	(*index)++;
	new_node->rchild = _TreeCreate(arr,size,index,null_node);
	return new_node;
}

TreeNode* TreeCreate(TreeDataType arr[],size_t size,TreeDataType null_node)
{
	int index = 0;
	return _TreeCreate(arr,size,&index,null_node);
}

测试用例：

//构造树测试
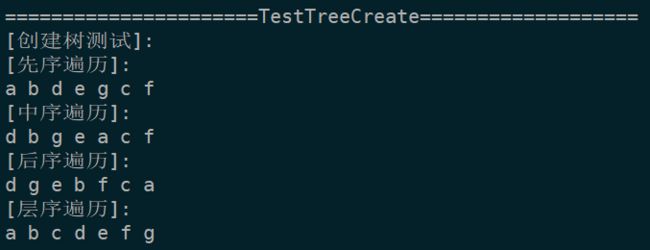
void TestTreeCreate()
{
	TITLE;
	printf("[创建树测试]:\n");
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	printf("\n");
	printf("[后序遍历]:\n");
	TreePostOrder(root);
	printf("\n");
	printf("[层序遍历]:\n");
	TreeLevelOrder(root);
}

运行结果：

销毁二叉树

销毁二叉树采用后序遍历，其原因是为了防止将根节点销毁后找不到其左右子树。

void TreeDestroy(TreeNode** root)
{
	if(root == NULL)
	{
		//非法输入
		return;
	}
	if(*root == NULL)
	{
		//空树
		return;
	}
	//后序销毁树
	TreeDestroy(&(*root)->lchild);
	TreeDestroy(&(*root)->rchild);
	DestroyNode(*root);
	*root = NULL;
	return;
}

测试用例：

//销毁树测试
void TestTreeDestroy()
{
	TITLE;
	printf("[销毁树测试]:\n");
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	TreeDestroy(&root);
	printf("expect is null,actul is %p\n",root);
}

运行结果：

克隆树

按照先序遍历克隆每一个结点即可。

      

TreeNode* TreeClone(TreeNode* root)
{
	if(root == NULL)
	{
		//非法输入
		return;
	}
	TreeNode* newNode = CreateTreeNode(root->data);	
	newNode->lchild = TreeClone(root->lchild);
	newNode->rchild = TreeClone(root->rchild);
	return newNode;
}

测试用例：

//克隆树测试
void TestTreeClone()
{
	TITLE;
	printf("[先创建一棵树]:\n");
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	printf("\n");
	printf("[后序遍历]:\n");
	TreePostOrder(root);
	printf("\n\n");

	printf("[克隆后]:\n");
	TreeNode* CloneTree = TreeClone(root);
	printf("[先序遍历]:\n");
	TreePreOrder(CloneTree);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(CloneTree);
	printf("\n");
	printf("[后序遍历]:\n");
	TreePostOrder(CloneTree);
	printf("\n");
}

运行结果：

树的基本概念

• 每个元素称为结点（node）；
• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 叶节点或终端节点：度为0的节点称为叶节点；
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 树的度：一棵树中，最大的节点的度称为树的度；
• 树的高度或深度：树中节点的最大层次；

求树的结点数

nt TreeSize(TreeNode* root)
{
	if(root == NULL)
	{
		//空树
		return 0;
	}
	if(root->lchild == NULL && root->rchild == NULL)
	{
		return 1;
	}
	return 1 + TreeSize(root->lchild) + TreeSize(root->rchild);	
}

求树的叶子结点

int TreeLeafSize(TreeNode* root)
{
	if(root == NULL)
	{
		//空树
		return 0;
	}
	if(root->lchild == NULL && root->rchild == NULL)
	{
		//此时说明该结点为叶子结点
		return 1;
	}
	return TreeLeafSize(root->lchild) + TreeLeafSize(root->rchild);
}

求第k层结点个数

//求第k层结点个数
//可将此问题转换为求根结点左右子树的k-1层结点数
int TreeKLevelSize(TreeNode* root, int k)
{
	if(root == NULL || k < 1)
	{
		//空树
		return 0;
	}
	if(k == 1)
	{
		return 1;
	}
	return TreeKLevelSize(root->lchild,k-1) + TreeKLevelSize(root->rchild,k-1);
}

求树的高度

//求树的高度
int TreeHeight(TreeNode* root)
{
	if(root == NULL)
	{
		//空树
		return 0;
	}
	if(root->lchild == NULL && root->rchild == NULL)
	{
		return 1;
	}
	int lHeight = TreeHeight(root->lchild);
	int rHeight = TreeHeight(root->rchild);
	//左右子树谁的高度高就返回谁的值
	return 1+(lHeight > rHeight ? lHeight : rHeight);
}

查找一个值

//查找一个值
//遍历二叉树即可，当发现与该值相等时返回该结点
//若没有则返回NULL
TreeNode* TreeFind(TreeNode* root, TreeDataType to_find)
{
	if(root == NULL)
	{
		//空树
		return NULL;
	}
	if(root->data == to_find)
	{
		return root;
	}
	TreeNode* lresult = TreeFind(root->lchild,to_find);
	TreeNode* rresult = TreeFind(root->rchild,to_find);
	//若左右子树均没有，返回值依然为空
	return lresult != NULL ? lresult : rresult;
}

返回一个结点的左子树

//返回一个结点的左子树
TreeNode* LChild(TreeNode* node)
{
	if(node == NULL)
	{
		return NULL;
	}
	return node->lchild;
}

返回一个结点的右子树

//返回一个结点的右子树
TreeNode* RChild(TreeNode* node)
{
	if(node == NULL)
	{
		return NULL;
	}
	return node->rchild;
}

返回一个结点的父结点

//返回一个结点的父结点
TreeNode* Parent(TreeNode* root, TreeNode* node)
{
	if(root == NULL)
	{
		return NULL;
	}
	if(root->lchild == node || root->rchild == node)
	{
		//说明此结点即为要找的结点的父结点
		return root;
	}
	TreeNode* lresult = Parent(root->lchild,node);
	TreeNode* rresult = Parent(root->rchild,node);
	return lresult != NULL ? lresult : rresult;
}

上面所有函数的测试用例：

void TestTreeSize()
{
	TITLE;
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	int ret = TreeSize(root);
	printf("\n[求树的结点数]:\n");
	printf("except is 7,actul is %d\n",ret);
}

void TestTreeLeafSize()
{
	TITLE;
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	int ret = TreeLeafSize(root);
	printf("\n[求树的叶子结点数]:\n");
	printf("except is 3,actul is %d\n",ret);
}

void TestTreeKLevelSzie()
{
	TITLE;
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	int ret = TreeKLevelSize(root,3);
	printf("\n[求树的第k层结点数]:\n");
	printf("except is 3,actul is %d\n",ret);
}

void TestTreeHeight()
{
	TITLE;
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	int ret = TreeHeight(root);
	printf("\n[求树的高度]:\n");
	printf("except is 4,actul is %d\n",ret);
}

void TestTreeFind()
{
	TITLE;
	//用数组中的元素内容创建一个二叉树(该数组满足树的前序遍历且包含空结点)
	char arr[] = "abd**eg***c*f**";
	TreeNode* root = TreeCreate(arr,sizeof(arr)/sizeof(arr[0]),'*');	
	printf("[先序遍历]:\n");
	TreePreOrder(root);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(root);
	TreeNode* to_find = TreeFind(root,'d');
	printf("\nFind d! expect is d,actul is %c\n",to_find->data);

	to_find = TreeFind(root,'A');
	printf("Not Find! expect is null,actul is %p\n",to_find);
}

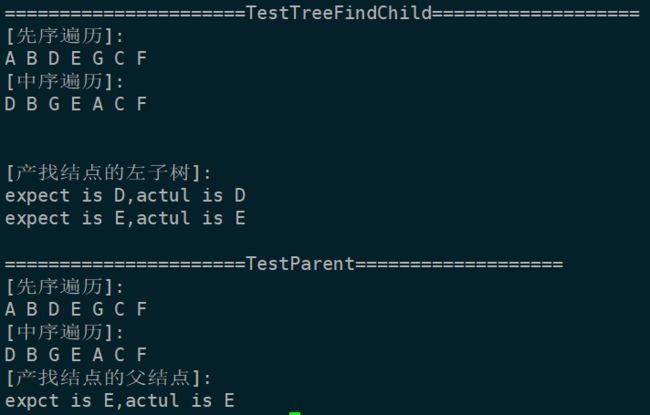
void TestTreeFindChild()
{
	TITLE;
	TreeNode* A = CreateTreeNode('A');
	TreeNode* B = CreateTreeNode('B');
	TreeNode* C = CreateTreeNode('C');
	TreeNode* D = CreateTreeNode('D');
	TreeNode* E = CreateTreeNode('E');
	TreeNode* F = CreateTreeNode('F');
	TreeNode* G = CreateTreeNode('G');
	
	A->lchild = B;
	A->rchild = C;
	B->lchild = D;
	B->rchild = E;
	C->rchild = F;
	E->lchild = G;

	printf("[先序遍历]:\n");
	TreePreOrder(A);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(A);
	printf("\n");
	printf("\n");
	printf("\n[产找结点的左子树]:\n");
	TreeNode* lchild = LChild(B);
	printf("expect is D,actul is %c\n",lchild->data);

	TreeNode* rchild = RChild(B);
	printf("expect is E,actul is %c\n",rchild->data);
}

void TestParent()
{
	TITLE;
	TreeNode* A = CreateTreeNode('A');
	TreeNode* B = CreateTreeNode('B');
	TreeNode* C = CreateTreeNode('C');
	TreeNode* D = CreateTreeNode('D');
	TreeNode* E = CreateTreeNode('E');
	TreeNode* F = CreateTreeNode('F');
	TreeNode* G = CreateTreeNode('G');
	
	A->lchild = B;
	A->rchild = C;
	B->lchild = D;
	B->rchild = E;
	C->rchild = F;
	E->lchild = G;

	printf("[先序遍历]:\n");
	TreePreOrder(A);
	printf("\n");
	printf("[中序遍历]:\n");
	TreeInOrder(A);
	
	printf("\n[产找结点的父结点]:\n");
	TreeNode* parentNode = Parent(A,G);
	printf("expct is E,actul is %c\n",parentNode->data);
}

运行结果：