每日题解:LeetCode 1457. 二叉树中的伪回文路径

题目地址
个人博客地址

题目描述

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

示例 1：

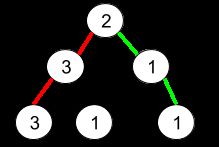
输入：root = [2,3,1,3,1,null,1]
输出：2 

解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。

示例 2：

输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1 

解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3：

输入：root = [9]
输出：1

提示：

给定二叉树的节点数目在 1 到 10^5 之间。
节点值在 1 到 9 之间。

解法

class Solution {
  private int ans = 0;

    public int pseudoPalindromicPaths(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int[] arr = new int[10];
        dfs(root, arr);
        return ans;
    }

    private void dfs(TreeNode node, int[] arr) {
        arr[node.val]++;
        if (node.left == null && node.right == null) {
        //判断是否是回文路径
            if (check(arr)) {
                ans++;
                arr[node.val]--;
                return;
            }
        }
        if (node.left != null) dfs(node.left, arr);
        if (node.right != null) dfs(node.right, arr);
        arr[node.val]--;
    }

    private boolean check(int[] arr) {
        int cnt = 0;
        for (int i = 0; i < arr.length; i++) {
            if ((arr[i]&1)==1) {
                cnt++;
            }
            if (cnt > 1) {
                return false;
            }

        }
        return true;
    }    
}

class Solution {
int ans=0;
    public int pseudoPalindromicPaths (TreeNode root) {
        if(root==null) return 0;
        helper(root,0);
        return ans;
    }
    
    void helper(TreeNode node,int temp){
        temp^=(1<<node.val);
        if(node.left==null&&node.right==null){
            if(temp==0||(temp&(temp-1))==0){
                ans++;
            }
        }
        if(node.left!=null) helper(node.left,temp);
        if(node.right!=null) helper(node.right,temp);
        return;
    }
    
}

解题思路

DFS (深度优先搜索算法)

题目要求根到叶子节点的所有路径是否存在回文路径，那就遍历二叉树，记录下全部节点值，判断是不是回文就可以了。

什么是回文路径？

根据回文序列性质, 可以知道, 最多只能有 1 个数字是奇数个(放在最中间), 其他字符都必须是偶数个，或者当然也可以所有数字都是偶数个。
那么只要记录下数字个个数，遍历数字的个数，当出现两个奇数个数就不是回文路径。由于题目规定节点值在 1 到 9 之间，那就简单了，定义一个长度为10的数组便可以了

int[] arr = new int[10];

遍历二叉树，当遍历到叶节点的时候，我们判断数组中，是否存在两个奇数的个数就可以了，
当判断结束后或者递归结束后，我们将将计数恢复成原始状态，避免对后面产生影响。

更优雅的做法？

我们知道n & (n - 1) 可以用来消除最后一个1，参考题目:位1的个数
a^b,如果a,b相等，结构为0，可以参考题目只出现一次的数字
所以回文路径只会有两种情况：

• 每个数字为个数为偶数，异或之后，结果为0。
• 每存在数字为奇数，异或之后，结果为个数为奇数的数字。
  所以我们判断条件可以改完

temp==0||(temp&(temp-1))==0

那怎么确保我们temp&(temp-1)的temp只有一个1，我们可以将数字放大，变成2的N次方。

1<<node.val