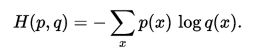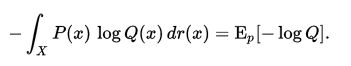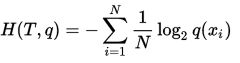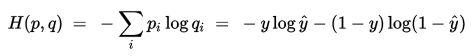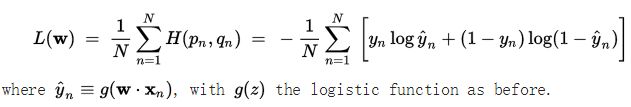深度学习之交叉熵损失函数的原理和应用

目录

 1、交叉熵的定义

 2、交叉熵的应用：

3、在逻辑回归中的应用

4.交叉熵和二次代价函数的对比

4.1. 二次代价函数的不足

4.2. 交叉熵代价函数

4.3 对数释然代价函数（log-likelihood cost）：

4.4 交叉熵代价函数是如何产生的？

5.实战

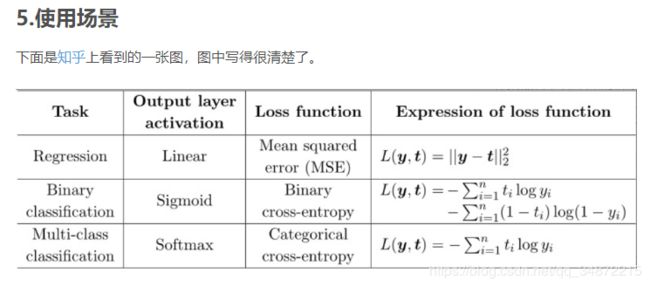
平方损失函数与交叉熵损失函数 适用的情况

---

 1、交叉熵的定义

在信息论中，交叉熵是表示两个概率分布p,q，其中p表示真实分布，q表示非真实分布，在相同的一组事件中，其中，用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中，我们很难理解交叉熵的定义。下面举个例子来描述一下：

假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。假如，按照真实分布p来衡量识别一个样本所需要的编码长度的期望为：

但是，如果采用错误的分布q来表示来自真实分布p的平均编码长度，则应该是:

此时就将H(p,q)称之为交叉熵。交叉熵的计算方式如下：

对于离散变量采用以下的方式计算：

对于连续变量采用以下的方式计算：

实际上，交叉熵是衡量两个概率分布p，q之间的相似性。这可以子啊特征工程中，用来衡量变量的重要性。

 2、交叉熵的应用：

（1）在特征工程中，可以用来衡量两个随机变量之间的相似度

（2）语言模型中（NLP），由于真实的分布p是未知的，在语言模型中，模型是通过训练集得到的，交叉熵就是衡量这个模型在测试集上的正确率。其计算方式如下：

　　　　

其中，N是表示的测试集的大小，q(x)表示的是事件x在训练集中的概率（在nlp中就是关键词在训练语料中的概率）。

3、在逻辑回归中的应用

由于交叉熵是衡量两个分布之间的相似度，在逻辑回归中，首先数据集真实的分布是p，通过逻辑回归模型预测出来的结果对应的分布是q，此时交叉熵在这里就是衡量预测结果q与真实结果p之间的差异程度，称之为交叉熵损失函数。具体如下：

假设，对应两分类的逻辑回归模型logistic regression来说，他的结果有两个0或者1，在给定预测向量x，通过logistics regression回归函数g(z)=1/(1+e-z),则真实结果y=1,对应预测结果y'=g(wx)；真实结果y=0，对应预测结果y'=1-g(wx);以上就是通过g(wx)和1-g(wx)来描述原数据集0-1分布。根据交叉熵的定义可知：

上式是针对测试集一个样本得到的交叉熵。若测试集有N个样本，对应的交叉熵损失函数表示方式如下：

 

4.交叉熵和二次代价函数的对比

4.1. 二次代价函数的不足

        ANN的设计目的之一是为了使机器可以像人一样学习知识。人在学习分析新事物时，当发现自己犯的错误越大时，改正的力度就越大。比如投篮：当运动员发现自己的投篮方向离正确方向越远，那么他调整的投篮角度就应该越大，篮球就更容易投进篮筐。同理，我们希望：ANN在训练时，如果预测值与实际值的误差越大，那么在反向传播训练的过程中，各种参数调整的幅度就要更大，从而使训练更快收敛。然而，如果使用二次代价函数训练ANN，看到的实际效果是，如果误差越大，参数调整的幅度可能更小，训练更缓慢。

        以一个神经元的二类分类训练为例，进行两次实验（ANN常用的激活函数为sigmoid函数，该实验也采用该函数）：输入一个相同的样本数据x=1.0（该样本对应的实际分类y=0）；两次实验各自随机初始化参数，从而在各自的第一次前向传播后得到不同的输出值，形成不同的代价（误差）：

实验1：第一次输出值为0.82

     

实验2：第一次输出值为0.98

 

        

        在实验1中，随机初始化参数，使得第一次输出值为0.82（该样本对应的实际值为0）；经过300次迭代训练后，输出值由0.82降到0.09，逼近实际值。而在实验2中，第一次输出值为0.98，同样经过300迭代训练，输出值只降到了0.20。

        从两次实验的代价曲线中可以看出：实验1的代价随着训练次数增加而快速降低，但实验2的代价在一开始下降得非常缓慢；直观上看，初始的误差越大，收敛得越缓慢。

        其实，误差大导致训练缓慢的原因在于使用了二次代价函数。二次代价函数的公式如下：

 

        其中，C表示代价，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。为简单起见，同样一个样本为例进行说明，此时二次代价函数为：

 

        目前训练ANN最有效的算法是反向传播算法。简而言之，训练ANN就是通过反向传播代价，以减少代价为导向，调整参数。参数主要有：神经元之间的连接权重w，以及每个神经元本身的偏置b。调参的方式是采用梯度下降算法（Gradient descent），沿着梯度方向调整参数大小。w和b的梯度推导如下：

 

        其中，z表示神经元的输入，表示激活函数。从以上公式可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。而神经网络常用的激活函数为sigmoid函数，该函数的曲线如下所示：

        假如我们目标是收敛到1。A点为0.82离目标比较远，梯度比较大，权值调整比较大。B点为0.98离目标比较近，梯度比较小，权值调整比较小。调整方案合理。 
        假如我们目标是收敛到0。A点为0.82离目标比较近，梯度比较大，权值调整比较大。B点为0.98离目标比较远，梯度比较小，权值调整比较小。调整方案不合理。

        如图所示，实验2的初始输出值（0.98）对应的梯度明显小于实验1的输出值（0.82），因此实验2的参数梯度下降得比实验1慢。这就是初始的代价（误差）越大，导致训练越慢的原因。与我们的期望不符，即：不能像人一样，错误越大，改正的幅度越大，从而学习得越快。

        可能有人会说，那就选择一个梯度不变化或变化不明显的激活函数不就解决问题了吗？图样图森破，那样虽然简单粗暴地解决了这个问题，但可能会引起其他更多更麻烦的问题。而且，类似sigmoid这样的函数（比如tanh函数）有很多优点，非常适合用来做激活函数，具体请自行google之。

4.2. 交叉熵代价函数

        换个思路，我们不换激活函数，而是换掉二次代价函数，改用交叉熵代价函数：

 

        其中，x表示样本，n表示样本的总数。那么，重新计算参数w的梯度：

 该等于在如下偏导的计算中，带入可以优化偏导，得到最终的结果

 

 

权值和偏置值的调整与无关。另外，梯度公式中表示输出值与实际值的误差。所以当误差越大时，梯度就越大，参数w和b的调整就越快，训练的速度也就越快。 
如果输出神经元是线性的，那么二次代价函数就是一种合适的选择。如果输出神经元是s型函数，那么比较适合用交叉熵代价函数。

---

4.3 对数释然代价函数（log-likelihood cost）：

对数释然函数通常用来作为softmax回归的代价函数，如果输出层神经元是sigmoid函数，可以采用交叉熵代价函数。而深度学习中更普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数释然函数。

对数释然函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数释然代价函数在二分类时可以化简为交叉熵代价函数的形式。

在TensorFlow中用： 
tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉熵。 
tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉熵。

4.4 交叉熵代价函数是如何产生的？

        以偏置b的梯度计算为例，推导出交叉熵代价函数：

 

        在第1小节中，由二次代价函数推导出来的b的梯度公式为：

 

        为了消掉该公式中的，我们想找到一个代价函数使得：

 

        即：

 

        对两侧求积分，可得：

 

        而这就是前面介绍的交叉熵代价函数。

5.实战

   对比交叉熵损失函数和二次代价函数的效果。

以MINST数据集分类 进行对比。

              结果分析：1.准确率达到0.9的时候，二次代价函数需要迭代7次。交叉熵只需要迭代2次。

                                2.同样迭代21次，二次代码函数达到的精确度为0.913，交叉熵达到的精度为0.92

             结论：在使用softmax和sigmoid一般与交叉熵搭配会有好的效果。

二次代价的准确率为：

Iter 0,Testing Accuracy 0.8286 
Iter 1,Testing Accuracy 0.8717 
Iter 2,Testing Accuracy 0.8816 
Iter 3,Testing Accuracy 0.8884 
Iter 4,Testing Accuracy 0.895 
Iter 5,Testing Accuracy 0.8966 
Iter 6,Testing Accuracy 0.8983 
Iter 7,Testing Accuracy 0.9013 
Iter 8,Testing Accuracy 0.9031 
Iter 9,Testing Accuracy 0.9048 
Iter 10,Testing Accuracy 0.9062 
Iter 11,Testing Accuracy 0.9073 
Iter 12,Testing Accuracy 0.908 
Iter 13,Testing Accuracy 0.9094 
Iter 14,Testing Accuracy 0.9098 
Iter 15,Testing Accuracy 0.9106 
Iter 16,Testing Accuracy 0.9118 
Iter 17,Testing Accuracy 0.9121 
Iter 18,Testing Accuracy 0.9132 
Iter 19,Testing Accuracy 0.9132 
Iter 20,Testing Accuracy 0.9139

 之后改用：

loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))

得到交叉熵的准确率：

Iter 0,Testing Accuracy 0.8249 
Iter 1,Testing Accuracy 0.8942 
Iter 2,Testing Accuracy 0.902 
Iter 3,Testing Accuracy 0.9058 
Iter 4,Testing Accuracy 0.9084 
Iter 5,Testing Accuracy 0.9102 
Iter 6,Testing Accuracy 0.9127 
Iter 7,Testing Accuracy 0.9135 
Iter 8,Testing Accuracy 0.9153 
Iter 9,Testing Accuracy 0.9159 
Iter 10,Testing Accuracy 0.917 
Iter 11,Testing Accuracy 0.9187 
Iter 12,Testing Accuracy 0.9193 
Iter 13,Testing Accuracy 0.92 
Iter 14,Testing Accuracy 0.9208 
Iter 15,Testing Accuracy 0.9203 
Iter 16,Testing Accuracy 0.9205 
Iter 17,Testing Accuracy 0.9205 
Iter 18,Testing Accuracy 0.922 
Iter 19,Testing Accuracy 0.9216 

Iter 20,Testing Accuracy 0.922

 

交叉熵和二次代价函数的区别：

           交叉熵调整权值和偏置值比较合理，当离目标点比较远时，调整的比较快；当离目标比较远时，调整的比较慢。

          二次代码函数，调整速度保持不变。

# coding: utf-8

# In[ ]:

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

#载入数据集
mnist = input_data.read_data_sets("MNIST_data",one_hot=True)

#每个批次的大小
batch_size = 100
#计算一共有多少个批次
n_batch = mnist.train.num_examples // batch_size

#定义两个placeholder
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])

#创建一个简单的神经网络
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x,W)+b)


#损失函数1、二次代价函数
# loss = tf.reduce_mean(tf.square(y-prediction))

#损失函数2、自定义损失函数（交叉熵）
 #tf.clip_by_value(A, min, max)：输入一个张量A，把A中的每一个元素的值都压缩在min和max之间。
 #小于min的让它等于min，大于max的元素的值等于max。
 #loss  = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))

#损失函数3、使用tensorflow自带的函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

#初始化变量
init = tf.global_variables_initializer()

#结果存放在一个布尔型列表中
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys =  mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})
        
        acc = sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
        print("Iter " + str(epoch) + ",Testing Accuracy " + str(acc))

 

平方损失函数与交叉熵损失函数 适用的情况

博客链接：https://blog.csdn.net/m_buddy/article/details/80224409

 

平方损失函数与交叉熵损失函数

交叉熵与均方差   https://blog.csdn.net/dawnranger/article/details/78031793

这里的categorical cross-entropy其实就是 log 似然损失函数。

机器学习中的损失函数  https://blog.csdn.net/rosenor1/article/details/52302217

为什么交叉熵可以作为损失函数？  https://blog.csdn.net/iloveyousunna/article/details/79205347

softmax和sigmoid以及SVM   https://blog.csdn.net/qq_35550465/article/details/82704189

对数损失函数是如何度量损失的？  https://www.zhihu.com/question/27126057

机器学习中常见的损失函数   https://www.cnblogs.com/houjun/p/8956384.html

以上图片来自： https://blog.csdn.net/hearthougan/article/details/82706834

softmax 交叉熵损失函数求导： https://www.jianshu.com/p/6e405cecd609

https://blog.csdn.net/qingyang666/article/details/70245855

https://www.cnblogs.com/klchang/p/9217551.html   对数损失函数(Logarithmic Loss Function)的原理和 Python 实现 

用于Multinoulli（多项分布）输出分布的softmax单元   https://blog.csdn.net/weixin_40516558/article/details/79962674

多项式分布及Softmax回归模型推导   https://blog.csdn.net/liuyhoo/article/details/81542100