激活函数总结sigmoid,tanh,relu,Leaky ReLU,RRelu,ELU,PRelu,SELU,swish

本文总结深度学习的损失函数及其优缺点。

激活函数是深度学习模型的重要成分，目的是将线性输入转换为非线性。常见的激活函数有sigmoid，tanh，ReLU等

1.sigmoid

Sigmoid 非线性函数将输入映射到 【0,1】之间。它的数学公式为：

历史上， sigmoid 函数曾非常常用，然而现在它已经不太受欢迎，实际很少使用了，因为它主要有两个缺点：

函数饱和使梯度消失

sigmoid 神经元在值为 0 或 1 的时候接近饱和，这些区域，梯度几乎为 0。因此在反向传播时，这个局部梯度会与整个代价函数关于该单元输出的梯度相乘，结果也会接近为 0 。

这样，几乎就没有信号通过神经元传到权重再到数据了，因此这时梯度就对模型的更新没有任何贡献。

除此之外，为了防止饱和，必须对于权重矩阵的初始化特别留意。比如，如果初始化权重过大，那么大多数神经元将会饱和，导致网络就几乎不学习。

sigmoid 函数不是关于原点中心对称的

这个特性会导致后面网络层的输入也不是零中心的，进而影响梯度下降的运作。

因为如果输入都是正数的话（如 x>0 中 ），那么关于 w的梯度在反向传播过程中，要么全是正数，要么全是负数（具体依据整个表达式f（x）而定），这将会导致梯度下降权重更新时出现 z 字型的下降。

当然，如果是按 batch 去训练，那么每个 batch 可能得到不同的信号，整个批量的梯度加起来后可以缓解这个问题。因此，该问题相对于上面的神经元饱和问题来说只是个小麻烦，没有那么严重。

2.tanh

tanh 函数同样存在饱和问题，但它的输出是零中心的，因此实际中 tanh 比 sigmoid 更受欢迎。

tanh 函数实际上是一个放大的 sigmoid 函数，数学关系为：

在具体应用中，tanh函数相比于Sigmoid函数往往更具有优越性，这主要是因为Sigmoid函数在输入处于[-1,1]之间时，函数值变化敏感，一旦接近或者超出区间就失去敏感性，处于饱和状态， 

3.Relu

近些年来非常流行。它的数学公式为：

ReLU 的效果如上图：

ReLU 的优点：

相较于 sigmoid 和 tanh 函数， ReLU 对于 SGD 的收敛有巨大的加速作用（Alex Krizhevsky 指出有 6 倍之多）。有人认为这是由它的线性、非饱和的公式导致的。

 

相比于 sigmoid/tanh ， ReLU 只需要一个阈值就可以得到激活值，而不用去算一大堆复杂的（指数）运算、

ReLU 的缺点是，它在训练时比较脆弱并且**可能“死掉”**。

举例来说：一个非常大的梯度经过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。如果这种情况发生，那么从此所有流过这个神经元的梯度将都变成 0 。

也就是说，这个 ReLU 单元在训练中将不可逆转的死亡，导致了数据多样化的丢失。实际中，如果学习率设置得太高，可能会发现网络中 40% 的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。

合理设置学习率，会降低这种情况的发生概率。

ReLU相比sigmoid和tanh的一个缺点是没有对上界设限.在实际使用中,可以设置一个上限,如ReLU6经验函数: f(x)=min(6,max(0,x))f(x)=min(6,max(0,x)).

4.Leaky ReLU

Leaky ReLU 是为解决“ ReLU 死亡”问题的尝试。

ReLU 中当 x<0 时，函数值为 0 。而 Leaky ReLU 则是给出一个很小的负数梯度值，比如 0.01 。

有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。

5.随机纠正线性单元（RReLU）

    “随机纠正线性单元”RReLU也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值。形式上来说，我们能得到以下结果：

    

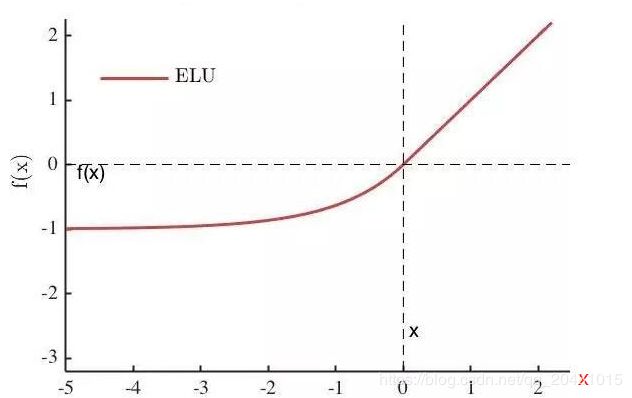
6.ELU

 

7.PRelu

PReLU(Parametric Rectified Linear Unit), 顾名思义：带参数的ReLU。二者的定义和区别如下图： 

如果ai=0，那么PReLU退化为ReLU；如果ai是一个很小的固定值(如ai=0.01)，则PReLU退化为Leaky ReLU(LReLU)。 有实验证明，与ReLU相比，LReLU对最终的结果几乎没什么影响。

PReLU的几点说明

（1） PReLU只增加了极少量的参数，也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的，当不同channels使用相同的ai时，参数就更少了。

（2） BP更新ai时，采用的是带动量的更新方式，如下：

8.SELU

经过该激活函数后使得样本分布自动归一化到0均值和单位方差(自归一化，保证训练过程中梯度不会爆炸或消失，效果比Batch Normalization 要好) 
其实就是ELU乘了个lambda，关键在于这个lambda是大于1的。以前relu，prelu，elu这些激活函数，都是在负半轴坡度平缓，这样在activation的方差过大的时候可以让它减小，防止了梯度爆炸，但是正半轴坡度简单的设成了1。而selu的正半轴大于1，在方差过小的的时候可以让它增大，同时防止了梯度消失。这样激活函数就有一个不动点，网络深了以后每一层的输出都是均值为0方差为1。

tensorflow中：tf.nn.selu(features, name=None)

 

9.Swish

Swish是Google在10月16号提出的一种新型激活函数,其原始公式为:f(x)=x * sigmod(x),变形Swish-B激活函数的公式则为f(x)=x * sigmod(b * x),其拥有不饱和,光滑,非单调性的特征,而Google在论文中的多项测试表明Swish以及Swish-B激活函数的性能即佳,在不同的数据集上都表现出了要优于当前最佳激活函数的性能.

参考地址：

https://www.cnblogs.com/ymjyqsx/p/6294021.html

https://blog.csdn.net/qq_23304241/article/details/80300149

https://www.colabug.com/3289623.html