LeetCode 第 21 场双周赛(779/1913,前40.7%)
文章目录
- 1. 比赛结果
- 2. 题目
- LeetCode 5336. 上升下降字符串 easy
- LeetCode 5337. 每个元音包含偶数次的最长子字符串 medium
- LeetCode 5338. 二叉树中的最长交错路径 medium
- LeetCode 5339. 二叉搜索子树的最大键值和 hard
1. 比赛结果
只做出来了第1题,第3题有一个例子超时,没解决
全国排名:779 / 1913,40.7%;全球排名:2027 / 4729,42.8%
2. 题目
LeetCode 5336. 上升下降字符串 easy
题目链接
给你一个字符串 s ,请你根据下面的算法重新构造字符串:
- 从 s 中选出 最小 的字符,将它 接在 结果字符串的后面。
- 从 s 剩余字符中选出 最小 的字符,且该字符比上一个添加的字符大,将它 接在 结果字符串后面。
- 重复步骤 2 ,直到你没法从 s 中选择字符。
- 从 s 中选出 最大 的字符,将它 接在 结果字符串的后面。
- 从 s 剩余字符中选出 最大 的字符,且该字符比上一个添加的字符小,将它 接在 结果字符串后面。
- 重复步骤 5 ,直到你没法从 s 中选择字符。
- 重复步骤 1 到 6 ,直到 s 中所有字符都已经被选过。
在任何一步中,如果最小或者最大字符不止一个 ,你可以选择其中任意一个,并将其添加到结果字符串。
请你返回将 s 中字符重新排序后的 结果字符串 。
示例 1:
输入:s = "aaaabbbbcccc"
输出:"abccbaabccba"
解释:第一轮的步骤 1,2,3 后,结果字符串为 result = "abc"
第一轮的步骤 4,5,6 后,结果字符串为 result = "abccba"
第一轮结束,现在 s = "aabbcc" ,我们再次回到步骤 1
第二轮的步骤 1,2,3 后,结果字符串为 result = "abccbaabc"
第二轮的步骤 4,5,6 后,结果字符串为 result = "abccbaabccba"
示例 2:
输入:s = "rat"
输出:"art"
解释:单词 "rat" 在上述算法重排序以后变成 "art"
示例 3:
输入:s = "leetcode"
输出:"cdelotee"
示例 4:
输入:s = "ggggggg"
输出:"ggggggg"
示例 5:
输入:s = "spo"
输出:"ops"
提示:
1 <= s.length <= 500
s 只包含小写英文字母。
解答:
- 一次遍历,对字符进行计数
- 正反遍历计数数组,直到计数全部为0
class Solution {
public:
string sortString(string s) {
int m[26] = {0}, sum = 0, i;
for(auto& ch : s)
{
m[ch-'a']++;
sum++;
}
string ans;
while(sum)
{
for(i = 0; i < 26; i++)
{
if(m[i])
{
ans.push_back(i+'a');
sum--;
m[i]--;
}
}
for(i = 25; i >= 0; i--)
{
if(m[i])
{
ans.push_back(i+'a');
sum--;
m[i]--;
}
}
}
return ans;
}
};
执行用时:12 ms
内存消耗:9.9 MB
LeetCode 5337. 每个元音包含偶数次的最长子字符串 medium
题目链接
给你一个字符串 s ,请你返回满足以下条件的最长子字符串的长度:每个元音字母,即 ‘a’,‘e’,‘i’,‘o’,‘u’ ,在子字符串中都恰好出现了偶数次。
示例 1:
输入:s = "eleetminicoworoep"
输出:13
解释:最长子字符串是 "leetminicowor" ,它包含 e,i,o 各 2 个,以及 0 个 a,u 。
示例 2:
输入:s = "leetcodeisgreat"
输出:5
解释:最长子字符串是 "leetc" ,其中包含 2 个 e 。
示例 3:
输入:s = "bcbcbc"
输出:6
解释:这个示例中,字符串 "bcbcbc" 本身就是最长的,因为所有的元音 a,e,i,o,u 都出现了 0 次。
提示:
1 <= s.length <= 5 x 10^5
s 只包含小写英文字母。
解题:
- 哈希map 记录所有元音字符的前缀异或值,及当前位置
- 当哈希表中可以查到该异或值时,说明当前位置与查到的位置之间的子串是满足题意的
举个例子:
"qacaba"
初始:没有元音,前缀异或值0,位置记为 -1;m[0] = -1
i = 0,没有元音,前缀异或值0,0 存在map,len = 0-(-1) = 1,最长“q”;
i = 1,出现元音a,前缀异或值a,位置 1;m[a] = 1
i = 2,没有元音,前缀异或值a,len = 2-m[a] = 1;
i = 3,出现元音a,前缀异或值a^a=0,len = 3-m[0] = 3-(-1) = 4,最长“qaca”;
i = 4,没有元音,前缀异或值0,len = 4-m[0] = 4-(-1)=5,最长“qacab”;
i = 5,出现元音a,前缀异或值0^a=a,len = 5-m[a] = 5-1 = 4,最长“caba”;
所以最长的是5个字符qacab
class Solution {
public:
int findTheLongestSubstring(string s) {
unordered_map<int,int> m; // 前缀异或值,对应的位置
int XOR = 0, i, maxlen = 0;
m[0] = -1; //没有元音,位置为-1,方便计算个数
for(i = 0; i < s.size(); i++)
{
if(s[i]!='a' && s[i]!='e' && s[i]!='i' && s[i]!='o' && s[i]!='u')
{
if(m.count(XOR))
maxlen = max(maxlen, i-m[XOR]);
}
else //s[i] 是元音
{
XOR ^= s[i];//元音异或值
if(m.count(XOR))
maxlen = max(maxlen, i-m[XOR]);
else
m[XOR] = i;
}
}
return maxlen;
}
};
or
class Solution {
public:
int findTheLongestSubstring(string s) {
unordered_map<int,int> m; // 前缀异或值,对应的位置
int XOR = 0, i, maxlen = 0;
m[0] = -1; //没有元音,位置为-1,方便计算个数
for(i = 0; i < s.size(); i++)
{
if(s[i]=='a' || s[i]=='e' || s[i]=='i' || s[i]=='o' || s[i]=='u')
XOR ^= s[i];//元音异或值
if(m.count(XOR))
maxlen = max(maxlen, i-m[XOR]);
else
m[XOR] = i;
}
return maxlen;
}
};
执行用时:184 ms
内存消耗:18.7 MB
LeetCode 5338. 二叉树中的最长交错路径 medium
题目链接
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
- 选择二叉树中 任意 节点和一个方向(左或者右)。
- 如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
- 改变前进方向:左变右或者右变左。
- 重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1(单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-zigzag-path-in-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题:
52 / 58 个通过测试用例
超时例子,代码如下:
class Solution {
int ans = 0;
public:
int longestZigZag(TreeNode* root) {
if(!root)
return 0;
dfs(root->left,0,0);
dfs(root->right,0,1);
longestZigZag(root->left);
longestZigZag(root->right);
return ans;
}
void dfs(TreeNode* root, int count, bool dir)
{
if(!root)
{
ans = max(ans,count);
return;
}
if(dir==true)
dfs(root->left,count+1,!dir);
else
dfs(root->right,count+1,!dir);
}
};
- 原因:主函数遍历了每个点,重复走了很多次
- 改:在调用的时候,遇到没变方向的,直接count计数置为 0 ,继续向下走。
class Solution {
int ans = 0;
public:
int longestZigZag(TreeNode* root) {
if(!root)
return 0;
dfs(root->left,0,0);
dfs(root->right,0,1);
return ans;
}
void dfs(TreeNode* root, int count, bool dir)
{
if(!root)
{
ans = max(ans,count);
return;
}
if(dir)//前一个是右节点
{
dfs(root->left,count+1,0);
dfs(root->right,0,1);
}
else//前一个是左节点
{
dfs(root->left,0,0);
dfs(root->right,count+1,1);
}
}
};
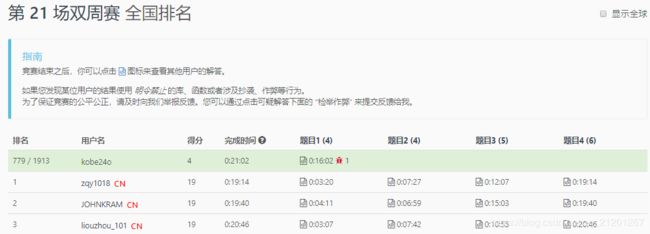
LeetCode 5339. 二叉搜索子树的最大键值和 hard
题目链接
给你一棵以 root 为根的 二叉树 ,请你返回 任意 二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
- 任意节点的左子树中的键值都 小于 此节点的键值。
- 任意节点的右子树中的键值都 大于 此节点的键值。
- 任意节点的左子树和右子树都是二叉搜索树。
解题:
参考大佬的解法:
- 自底向上,返回4个变量的 vector
- 【0】是不是搜索树【1】左子树最小值【2】右子树最大值【3】子树val 的 sum
- 空节点 返回
{true,INT_MAX,INT_MIN,0} - 获得左右子树的状态后,开始判断:
- 都必须是搜索树,左子树最大值小于 root,右子树最小值 大于 root,全部满足,才是搜索树
class Solution {
int maxSum = 0;
public:
int maxSumBST(TreeNode* root) {
dfs(root);
return maxSum;
}
vector<int> dfs(TreeNode* root)
{
if(!root)
return {true,INT_MAX,INT_MIN,0};
//子树是不是二叉搜索树 vec[0]
//子树的最小值 vec[1]
//子树的最大值 vec[2]
//子树的sum值 vec[3]
auto Lstate = dfs(root->left);
auto Rstate = dfs(root->right);
if(!Lstate[0] || !Rstate[0] || Lstate[2] >= root->val
|| Rstate[1] <= root->val)
return {false,INT_MAX,INT_MIN,0};//后三个参数随意
//是二叉搜索树
int Lmin = root->left ? Lstate[1] : root->val;
int Rmax = root->right ? Rstate[2] : root->val;
int cursum = root->val+Lstate[3]+Rstate[3];
maxSum = max(maxSum, cursum);
return {true,Lmin,Rmax,cursum};
}
};