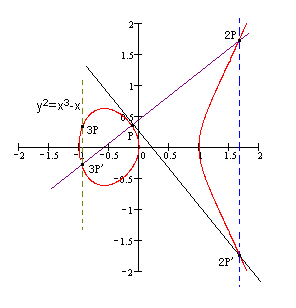现在很多基于区块链技术的数字货币系统，比如：比特币和以太坊，它们都使用了椭圆曲线密码学(ECC, Elliptic Curve Cryptography)来保证货币的安全性。

ECC 是一种公开密钥密码学，又称为非对称密码学。在这种密码学中，需要产生一对密钥。其中一个密钥称为私钥，需要保密；另一个密钥称为公钥，是可以公开让别人知道的。

私钥和公钥在数学上的关系是不可逆的，也就是通过某个数学函数，我们可以从私钥计算出公钥，但是不能从公钥反向推导出私钥(或者说从计算上是不可行的)。

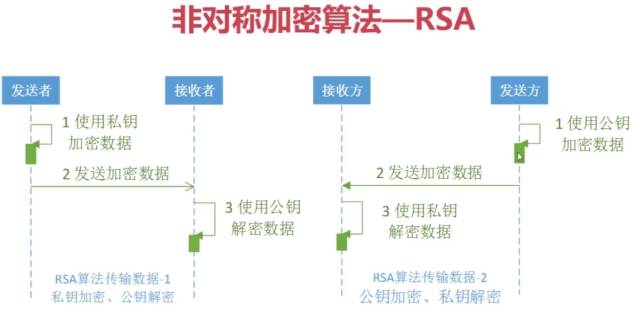
非对称加密算法

椭圆曲线加密算法对应的数学函数是椭圆曲线乘法，而另一种广泛使用的非对称加密算法 RSA (由三个发明人姓氏的开头字母组成)对应的数学函数是极大整数的因式分解。

与对称密码学使用相同的密钥进行加解密不同，非对称密码学有一个很有用的特性：如果用公钥对数据进行加密，只有用对应的私钥才能解密；如果用私钥对数据进行加密，那么只有用对应的公钥才能解密。

椭圆曲线的运算

一听说椭圆曲线，很多人会凭直觉认为这条数学曲线像个椭圆，其实不然。椭圆曲线因为用二元三次方程y2= x3+ ax + b来表示，类似椭圆周长计算方程而得名。以下是比特币的椭圆曲线图，是不是一点也不像椭圆：

椭圆周长方程

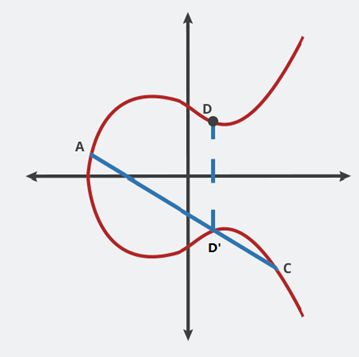
椭圆曲线上点的加法定义：任意取椭圆曲线上两点 A、C （若 A、C 两点重合，则做 A 点的切线）做直线交于椭圆曲线的另一点 D'，过 D'做 y 轴的平行线交于 D。在这里我们规定 A+C=D。

k 个相同的点 P 相加，我们记作 kP。如下图：P+P+P = 2P+P = 3P。

如果我们定义K=kG， k 为整数，G 为椭圆曲线上的一个点，该等式就是表示 k 个 G 点相加或 k 乘以G 得到的结果为点 K，K 也为椭圆曲线上的一个点。

我们可以用这个等式中的k 作为私钥，而结果点K 作为公钥。G 为该椭圆曲线的基点，和参数 a，b 都是公开的。

已知整数 k 和基点 G，根据椭圆曲线加法法则，推算出点 K 是非常容易的，因为存在快速算法可以将计算复杂度降低到O(logk)。

私钥推导出公钥的过程是不可逆的，即现在数学上还没有有效的方法可以从基点 G 和点 K 推算出整数 k。如果使用遍历法来寻找整数 k，其计算复杂度为O(k)。在实际使用时，整数 k 会取一个非常大的值。

比如： k 为一个78位的十进制数，由私钥推算出公钥的计算复杂度为O(78)，用遍历法从公钥找出私钥的计算复杂度为O(1078)，而宇宙中已知的原子总数大概为1080，所以采用暴力破解法破解私钥是根本不可行的。

为了让椭圆曲线更形象易理解，我们上面画的曲线都是连续的，实际用于加密的曲线都是有限域上定义的离散曲线。

随着椭圆曲线参数 a、 b，基点 G的不同，椭圆曲线的加密性能也不一样。为了获得更高的安全性，对这些参数也有一些特定的要求。

我们会给一些常用的使用特定参数的椭圆曲线取一个名字。比如：美国国家标准与技术研究院(NIST)和美国国家安全局(NSA)推荐过的 secp256r1、secp521r1 等椭圆曲线（有些开源社区怀疑这些曲线中参数有可能被精心选取，导致曲线加密性能弱化），中国国家密码局认定的 SM2 国产密码算法。

比特币和以太坊使用的椭圆曲线是 secp256k1。该曲线的参数非常简单(人们相信不是为了设计一条弱曲线而被精心构造的)：

（ secp256k1 的 a、b 以及基点 G）

与传统的 RSA 算法相比，严格选定参数的 ECC 有更强的安全性，不易被攻击。

1）破解相同位数密钥所需能量：

有科学家通过计算攻破一个密码学算法需要多少能量并把它与水沸腾需要多少能量对比来衡量一个加密算法的安全性。

经过他的分析，破解一个228位的 RSA 密钥需要的能量少于煮沸一汤勺水的能量。而破解一个228位的椭圆曲线密钥需要足够煮沸地球上所有水的能量。

RSA 要达到一个安全的水平，需要一个至少2380位的密钥。此外RSA 算法还有一个缺点就是随着密钥长度的增加，其安全性的增益是减少的。这意味着我们无法通过不断增加密钥长度来获得更高的安全性。

2）性能对比：

另一方面，使用椭圆曲线签名算法(ECDSA)做签名的性能也比 RSA 签名算法高很多。根据某些研究结果，在获得相同的安全性时，前者要比后者快20多倍。

椭圆曲线加密算法能够以更短的密钥获取与其他加密算法相同的安全性及更快的运算速度，所以 ECC 正在快速成为网络隐私和安全的首选解决方案。比特币等数字货币系统也纷纷使用 ECC 作为其安全性的基石。

下面我们简单说说椭圆曲线密码学在比特币中的用法。

在比特币中，用户生成一个随机整数 k (256位二进制数)作为其账户私钥，而用对应的公钥 K(K=kG) 的哈希值作为其账户的比特币地址。

（私钥与地址的关系）

用户需要使用其账户比特币地址上的货币时，只需要提供一个用其私钥对地址金额等信息计算出的签名和对应的公钥。其他比特币用户就可以在只知道该用户公钥的情况，验证该签名是否有效，从而判断该用户是否真正拥有该地址上的货币。

攻击者因为无法通过其公钥或比特币地址来推算出私钥，也就无法伪造出一个有效的签名来盗用其账户上的货币。

另：在生成私钥 k 的过程中，确保 k 是真正随机生成的非常重要。曾经有些厂商的随机数生成算法因为有漏洞或者故意留有后门，造成了巨大的安全隐患。

本文作者：肖诗源（点融黑帮），现就职于点融网工程部区块链团队。华中科技大学博士毕业，在美国国家标准与技术研究院(NIST)做过短期访问学者，后在爱立信工作10年，获批8项专利。喜欢旅游和科幻电影。