pytorch——计算图与动态图机制

1、计算图

计算图是用来描述运算的有向无环图；

计算图有两个主要元素：结点（Node）和边（Edge）；

结点表示数据，如向量、矩阵、张量，边表示运算，如加减乘除卷积等；

用计算图表示：$y=(x+w)\ast (w+1)$
令$a=x+w$，$b=w+1$，$y=a\ast b$，那么得到的计算图如下所示：

采用计算图来描述运算的好处不仅仅是让运算更加简洁，还有一个更加重要的作用是使梯度求导更加方便。举个例子，看一下y对w求导的一个过程。

计算图与梯度求导

$y=(x+w)\ast (w+1)$
$a=x+w$ $b=w+1$
$y=a\ast b$

$\frac{\partial y}{\partial w}=\frac{\partial y}{\partial a}\frac{\partial a}{\partial w}+\frac{\partial y}{\partial b}\frac{\partial b}{\partial w}$
$=b\ast 1+a\ast 1$
$=b+a$
$=(w+1)+(x+w)$
$=2\ast w+x+1$
$=2\ast 1+2+1$
$=5$

通过链式求导可以知道，利用计算图推导得到的推导结果如下图所示：

通过分析可以知道，y对w求导就是在计算图中找到所有y到w的路径，把路径上的导数进行求和。

利用代码看一下y对w求导之后w的梯度是否是上面计算得到的。具体的代码如下所示：

import torch

w = torch.tensor([1.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True
x = torch.tensor([2.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True

a = torch.add(w, x)     # a = w + x
b = torch.add(w, 1)     # b = w + 1
y = torch.mul(a, b)     # y = a * b

y.backward()    #对y进行反向传播
print(w.grad)   #输出w的梯度

得到的结果为5，证明了上面的结论。

在第一篇博文中讲张量的属性的时候，讲到与梯度相关的四个属性的时候，有一个is_leaf，也就是叶子节点，叶子节点的功能是指示张量是否是叶子节点。

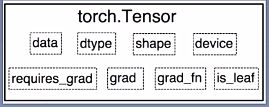
叶子节点：用户创建的结点称为叶子结点，如X与W；
is_leaf：指示张量是否为叶子节点；

叶子节点是整个计算图的根基，例如前面求导的计算图，在前向传导中的a、b和y都要依据创建的叶子节点x和w进行计算的。同样，在反向传播过程中，所有梯度的计算都要依赖叶子节点。

设置叶子节点主要是为了节省内存，在梯度反向传播结束之后，非叶子节点的梯度都会被释放掉。可以根据代码分析一下非叶子节点a、b和y的梯度情况。

import torch

w = torch.tensor([1.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True
x = torch.tensor([2.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True

a = torch.add(w, x)     # a = w + x
b = torch.add(w, 1)     # b = w + 1
y = torch.mul(a, b)     # y = a * b

y.backward()    #对y进行反向传播
print(w.grad)   #输出w的梯度

#查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)  #输出为True True False False False，只有前面两个是叶子节点

#查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)  #输出为tensor([5.]) tensor([2.]) None None None，因为非叶子节点都被释放掉了

如果想使用非叶子结点梯度，可以使用pytorch中的retain_grad()。例如对上面代码中的a执行相关操作a.retain_grad()，则a的梯度会被保留下来，具体的代码如下所示：

import torch

w = torch.tensor([1.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True
x = torch.tensor([2.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True

a = torch.add(w, x)     # a = w + x
a.retain_grad()   #保存非叶子结点a的梯度，输出为tensor([5.]) tensor([2.]) tensor([2.]) None None
b = torch.add(w, 1)     # b = w + 1
y = torch.mul(a, b)     # y = a * b

y.backward()    #对y进行反向传播
print(w.grad)   #输出w的梯度

#查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

#查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

torch.Tensor中还有一个属性为grad_fn，grad_fn的作用是记录创建该张量时所用的方法（函数），该属性在梯度反向传播的时候用到。例如在上面提到的例子中，y.grad_fn = ，y在反向传播的时候会记录y是用乘法得到的，所用在求解a和b的梯度的时候就会用到乘法的求导法则去求解a和b的梯度。同样，对于a有a.grad_fn=，对于b有b.grad_fn=，由于a和b是通过加法得到的，所以grad_fn都是AddBackword0。可以通过代码观看各个变量的属性。

import torch

w = torch.tensor([1.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True
x = torch.tensor([2.], requires_grad=True)  #由于需要计算梯度，所以requires_grad设置为True

a = torch.add(w, x)     # a = w + x
a.retain_grad()
b = torch.add(w, 1)     # b = w + 1
y = torch.mul(a, b)     # y = a * b

y.backward()    #对y进行反向传播
print(w.grad)   #输出w的梯度

# 查看 grad_fn
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

#上面代码的输出结果为
grad_fn:
 None None <AddBackward0 object at 0x000001EEAA829308> <AddBackward0 object at 0x000001EE9C051548> <MulBackward0 object at 0x000001EE9C29F948>

可以看到w和x的grad_fn都是None，因为w和x都是用户创建的，没有通过任何方法任何函数去生成这两个张量，所以两个叶子节点的属性为None，这些属性都是在梯度求导中用到的。
2、pytorch的动态图机制

动态图 vs 静态图

动态图：pytorch使用的，运算与搭建同时进行；灵活，易调节。
静态图：tensorflow使用的，先搭建图，后运算；高效，不灵活。

根据计算图搭建方式，可将计算图分为动态图和静态图。

为了尽快理解静态图和动态图的区别，这里举一个例子。假如我们去新马泰旅游，如果我们是跟团的话就是静态图，如果是自驾游的话就是动态图。跟团的意思是路线都已经计划好了，也就是先建图后运算。自驾游的话可以根据实际情况实际调整。下面分别列举tensorflow的静态图例子和pytorch的动态图实例进行简单理解。

在上面这个图中，框框代表的就是节点，带箭头的线代表边。tensorflow使用的是静态图，是先将图搭建好之后，再input数据进去。

pytorch使用的是动态图，具体的操作如下代码：

W_h = torch.randn(20, 20, requires_grad=True)  #先创建四个张量
W_x = torch.randn(20, 10, requires_grad=True)
x = torch.randn(1, 10)
prev_h = torch.randn(1, 20)

h2h = torch.mm(W_h, prev_h.t())   #将W_h和prev_h进行相乘，得到一个新张量h2h
i2h = torch.mm(W_x, x.t())  #将W_x和x进行相乘，等到一个新张量i2h
next_h = h2h + i2h  #创建加法操作
next_h = next_h.tanh() #使用激活函数

loss = next_h.sum()   #计算损失函数
loss.backward()   #梯度反向传播

上面代码对应的动态图过程就是下面的图

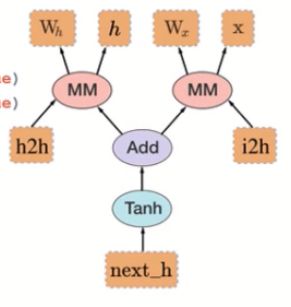
动态图的搭建是根据每一步的计算搭建的，而tensorflow是先搭建所有的计算图之后，再把数据输入进去。这就是动态图和静态图的区别。