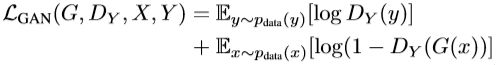生成对抗网络(四)CycleGAN讲解
生成对抗网络CycleGAN讲解
- Abstract
- 1. Introduction
- 2. Related Work
- 3. Formulation
- 3.1. Adversarial Loss
- 3.2. Cycle Consistency Loss
- 3.3. Full Objective(汇总)
- 4. 训练细节:
- Reference

原文:Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
收录:2017
代码:Pytorch

这次工作则是将无配对的图像进行图像之间转换,例如你有画家作品以及自然照片之类,想将照片转化成画家风格,但这两张图片之间没有任何交集却也能转化成功,其中具体实现在下面详细讲述。
Abstract
图像到图像的转换是一类视觉和图像的问题,其目标就是用大量相配对的图像作为训练集,学习到输入图像到输出图像的映射。但是,成对的训练数据无法得到。虽然数据缺乏,但我们还是提出了从图像X转换到图像Y的方法。细化来说则是,使用对抗损失函数来学习映射G:X → Y,让判别器难以区分图片 G(X) 与 Y。
由于这样的映射高度欠约束,于是添加了一个逆映射F: Y → X的,并引入一个循环一致性损失函数(cycle consistency loss)来确保F(G(X)) ≈ X(反之亦然)。
在不存在成对训练数据的情况下,对风格迁移、物体变形、季节转换、照片增强等任务进行定性分析。通过与已有方法的定量比较,证明了该方法的优越性。
※论文核心思想:
- 循环一致损失函数 以及 对抗损失函数
1. Introduction
尽管缺乏成对的监督学习样本,我们仍然可以在集合层面使用监督学习:给定数据域X中的一组图像,和Y 域中的另外一组图像。我们可以训练一种映射G:X → Y 使得得出 y ^ = G ( x ) , x ∈ X \hat{y}=G(x),x\in X y^=G(x),x∈X ,同时判别器不断将生成的样本 y ^ \hat{y} y^ 从真实样本 y 中辨认出来。因此存在一个最佳的映射 G* 将数据域 X 转换为数据域 Y ^ \hat{Y} Y^ ,使得 Y ^ ≈ Y \hat{Y}\approx Y Y^≈Y (即有相同的分布)。然而, 由输入x到导出相同的 y 这样的映射有无数种,因此不能确保这一对最有意义 。此外,在实际中我们 很难单独地优化判别器 ,当所有的输入图像映射到相同的输出图像的时候,标准的程序经常因为一些问题而导致奔溃,使得优化无法继续。
为了解决上述问题,我们引入了“循环一致”性质,通俗来讲则是从英语翻译到中文,再从中文翻译回来,结果得到一样的句子,即G:X → Y,F:Y → X 并且引入一个循环一致损失函数(cycle consistency loss) 使得 F ( G ( X ) ) ≈ x F(G(X))\approx x F(G(X))≈x 以及 G ( F ( y ) ) ≈ y G(F(y))\approx y G(F(y))≈y。将这个循环一致损失函数与在数据域X 与数据域Y 中判别器的对抗损失函数结合起来,就可以得到非成对图像到图像的目标转换。
2. Related Work
GAN: 其核心就是通过对抗损失(adversarial loss)来促使生成器G生成图像无法与真实图像区分开。因此我们采用对抗损失来学习映射,会使得转换后的图片难以和目标域的图像区分开。
Image-to-Image Translation:这个想法追溯到Hertzmann的 图像类比 (Image Analogies),这个模型在一对输入输出的训练图像上采用了非参数的纹理模型,我们的研究建立在 Isola 的 pix2pix 框架上,该框架使用了CGAN来学习从输入到输出的映射,与先前的工作不同,我们可以从不成对的训练图片中,学习到这种映射。
Unpaired Image-to-Image Translation:Rosales 提出了一个贝叶斯框架,通过对原图像以及从多风格图像中得到的似然项 (likelihood term) 进行计算,得到一个基于区块 (patch-based)、基于先验信息的马尔可夫随机场;更近一点研究, CoGAN 和 跨模态场景网络 (corss-modal scene networks) 使用了权重共享策略去学习跨领域 (across domains) 的共同表示等。
Cycle Consistency: Zhou et al. 和 Godard et al两篇文章的与我的工作比较相似,他们也使用了循环一致性损失体现传递性,从而监督卷积网络的训练。
Neural Style Transfer:神经网络风格迁移是优化 图像到图像转换 的另外一种方法,通过比较不同风格的两种图像(一张是普通图片,另一张是另外一种风格的图片(一般来讲是绘画作品))并将一幅图像的内容和另一幅的风格组合起来,基于预训练期间对伽马矩阵进行统计从而得到深层次的特征,再对这些特征进行匹配,最终合成新图像。
另一方面,我们主要关注的是:通过刻画更高层级外表结构之间的对应关系,学习两个图像集之间的映射,而不仅是两张特定图片之间的映射。
3. Formulation
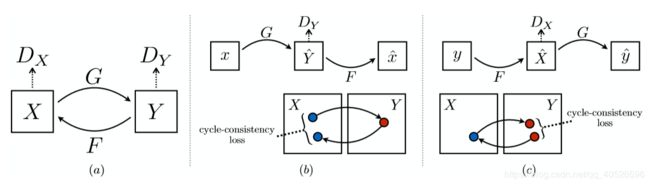
如上图(a)可知 D X D_{X} DX则是能将数据集X中的x和F(y)能区分出来;而且 D Y D_{Y} DY则是能将数据集Y中的y和G(x)能区分出来。接下来将介绍循环一致损失函数和对抗损失函数。
3.1. Adversarial Loss
① G:X→ Y的对抗损失:
G的目标是将这个目标最小化,而D的目标是最大化,因此 m i n G m a x D y L G A N ( G , D Y , X , Y ) min_{G}max_{D_{y}}L_{GAN}(G,D_{Y},X,Y) minGmaxDyLGAN(G,DY,X,Y)
② F:Y→ X的对抗损失:
L G A N ( F , D X , Y , X ) = E x ∼ p d a t a ( x ) [ l o g D X ( x ) ] + E y ∼ p d a t a ( y ) [ 1 − l o g D X ( F ( y ) ) ] L_{GAN}(F,D_{X},Y,X)=E_{x\sim p_{data}(x)}[logD_{X}(x)]+E_{y\sim p_{data}(y)}[1-logD_{X}(F(y))] LGAN(F,DX,Y,X)=Ex∼pdata(x)[logDX(x)]+Ey∼pdata(y)[1−logDX(F(y))]
同样F的目标是将这个目标最小化,而D的目标是最大化,因此 m i n F m a x D x L G A N ( G , D Y , Y , X ) min_{F}max_{D_{x}}L_{GAN}(G,D_{Y},Y,X) minFmaxDxLGAN(G,DY,Y,X)
详细解释参考GAN的对抗损失函数部分。
3.2. Cycle Consistency Loss
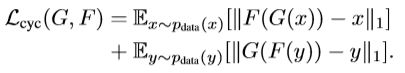
为了使得y → F(y) → G(F(y)) ≈ y, x → G(x) → F(G(x)) ≈ x 。
3.3. Full Objective(汇总)
完整的模型公式如下,其中,λ 控制两个对象的相对重要性。
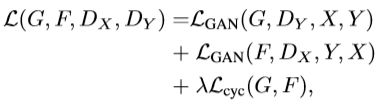
我们希望解决映射的学习问题:
![]()
4. 训练细节:
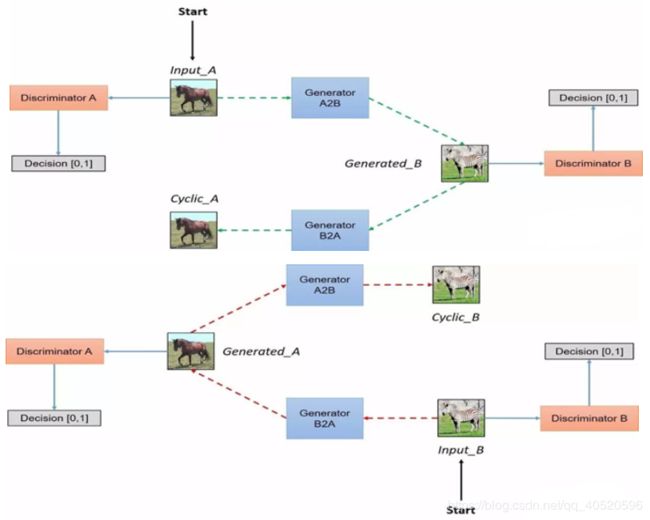
CycleGAN的生成器采用U-Net,判别器采用LS-GAN。
- Generator采用的是Perceptual losses for real-time style transfer and super-resolution 一文中的网络结构;一个resblock组成的网络,降采样部分采用stride 卷积,增采样部分采用反卷积;Discriminator采用的仍是pix2pix中的PatchGANs结构,大小为70x70;
- 定义四个xx器的损失函数,分别优化训练G和D,两个生成器共享权重,两个鉴别器也共享权重训练
- 计算每个生成图像的损失是不可能的,因为会耗费大量的计算资源。建立一个图像库,存储之前生成的50张图,而不只是最新的生成器生成的图
- Lr=0.0002。对于前100个周期,保持相同的学习速率0.0002,然后在接下来的100个周期内线性衰减到0。
Reference
- CycleGAN论文的阅读与翻译,无监督风格迁移
- CycleGan论文笔记