softmax算法与损失函数的综合应用
6.5 softmax 算法与损失函数的综合应用
在神经网络中使用 softmax 计算 loss 时对于初学者常常会范很多错误,下面通过具体的实
例代码演示需要注意哪些关键的地方与具体的用法。
6.5.1 实例 22 交叉熵实验
对于交叉熵这个比较生僻的术语,在深度学习领域中是最常见不过了,由于其常用性,在
TensorFlow 中会被封装成为多个版本, 有的公式里直接带了交叉熵,有的需要自己单独求一下
交叉熵,而在构建模型时,如果这块知识不扎实,出现问题时很难分析是模型的问题还是交叉熵
的使用问题。 这里有必要通过几个小实验将其弄得更明白一些。
案例描述
下面一段代码,假设有一个标签 labels 和一个网络输出值 logits。
这个案例就是以这两个值来进行以下 3 次实验:
(1)两次 softmax 实验:将输出值 logits 分别进行 1 次和 2 次 softmax,观察两次的区别
及意义;
(2)观察交叉熵:将上个步骤中的两个值分别进行 softmax_cross_entropy_with_logits,
观察区别;
(3)自建公式实验:将做两次 softmax 的值放到自建组合的公式里得到正确的值。
代码 6-1 softmax 应用
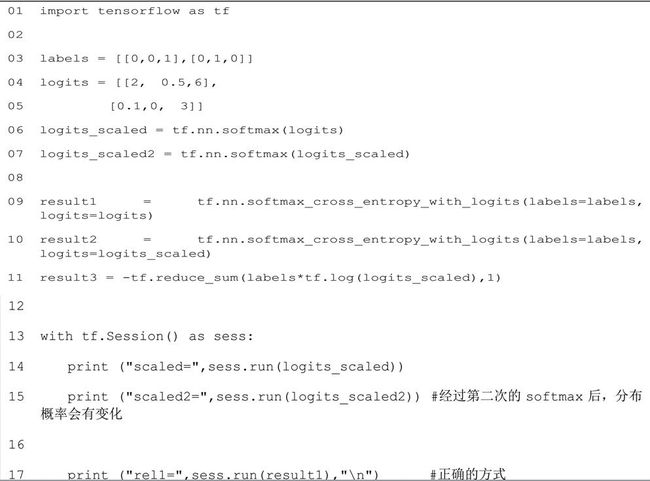

可以看到: logits 里面的值原本加和都是大于 1 的,但是经过 softmax 之后,总和变成了 1。
样本中第一个是跟标签分类相符的,第二与标签分类不符,所以第一个的交叉熵比较小为
0.02215516,而第二个比较大 3.09967351。
下面开始验证下前面说所的实验:
● 比较 scaled 和 scaled2 可以看到:经过第二次的 softmax 后,分布概率会有变化,而
scaled 才是我们真实转化的 softmax 值。
● 比较 rel1 和 rel2 可以看到:传入 softmax_cross_entropy_with_logits 的 logits 是
不 需 要 进 行 softmax 的 。 如 果 将 softmax 后 的 值 scaled 传 入softmax_cross_entropy_with_logits 就相当于进行了两次的 softmax 转换。
对于已经用 softmax 转换过的 scaled,在计算 loss 时就不能在用 TensorFlow 里面的softmax_cross_entropy_with_logits 了。读者可以自己写一个 loss 的函数,参见 rel3 的生成,通过自己组合的函数实现了 softmax_cross_entropy_with_logits 一样的结果。
6.5.2实例 23:one_hot 实验
其实输入的标签也可以不是标准的 one-hot, 下面用一组总和也为 1 但是每个都不等于 0 或1 的数组来代替标签,看看效果。
案例描述
对非 one-hot 编码为标签的数据进行交叉熵的计算,比较其与 one-hot 编码的交熵之间的差别。
接上述代码,将标签换为[[0.4,0.1,0.5],[0.3,0.6,0.1]]与原始的[[0,0,1], [0,1,0]]代
表的分类意义等价,将这个标签代入交叉熵。
代码 6-1 softmax 应用(续)

运行上面代码,生成如下结果:

比较前面的 rel1 发现,对于正确分类的交叉熵和错误分类的交叉熵,二者的结果差别没有
标准 one-hot 那么明显。
6.5.3 实例 24: sparse 交叉熵使用
下面再举个例子看一下 sparse_softmax_cross_entropy_with_logits 的用法,它需要使用
非 one-hot 的标签。所以,要把前面的标签换成具体数值[2,1],具体代码如下。
案例描述
演示使用 sparse_softmax_cross_entropy_with_logits 函数,对非 one-hot 的标签进行交
叉熵计算,比较其与 one-hot 标签在使用上的区别。

发现 rel5 与前面的 rel1 结果完全一样。
6.5.4 实例 25:计算 loss 值
在真正的神经网络中,得到这样的一个数组并不能满足要求,还需要对其求均值,使其最终
变成一个具体的数值,如下代码。
案例描述
演示通过分别对上文交叉熵结果 result1 与 softmax 后的结果 logits_scaled 计算 loss,
验证如下结论:
(1)对于 softmax_cross_entropy_with_logits 后的结果求 loss 直接取均值;
(2)对于 softmax 后的结果使用-tf.reduce_sum(labels * tf.log(logits_scaled))求 loss。
(3)对于 softmax 后的结果使用-tf.reduce_sum(labels*tf.log(logits_scaled),1)等同于
softmax_cross_entropy_with_logits 结果。
(4)由 1 和 3 可以推出对 3 进行求均值也可以得出正确的 loss 值,合并起来的公式为:
tf.reduce_sum(-tf.reduce_sum(labels*tf.log(logits_scaled),1)) =loss(该结论是由前
面的验证推导出来,有兴趣的读者可以自行验证)

这便是我们最终要得到的损失值了。
运行上面代码输出结果如下:

与 loss 的值完全吻合。
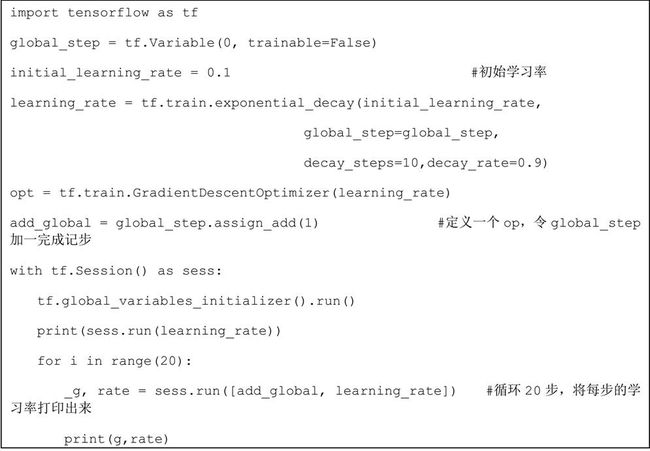
6.6.4 实例 26:退化学习率的用法举例
本例子主要是演示学习率衰减的使用方法。
例子中使用了迭代循环计数变量 global_step 来标记循环次数,初始学习率为 0.1,令其以
每 10 次衰减 0.9 的速度来进行退化。
案例描述
定义一个学习率变量,将其衰减系数设置好,并设置好迭代循环的次数,将每次迭代运算的
次数与学习率打印出来,观察学习率按照次数退化的现象。
6.8.2 实例 27:用 Maxout 网络实现 Mnist 分类
本例子主要是演示 Maxout 网络的构建方法。
例 子 中 , 拿 6.5 节 的 练习 题 答 案 来 修 改 代 码 ,在 本 书 附 带 资 源 中 的 “ 代 码 6-2sparesoftmaxwithminist.py” 里面做如下改动。
案例描述
Maxout 网络的构建方法:通过 reduce_max 函数对多个神经元的输出来计算 Max 值,将 Max
值通过另一套学习参数计算得到最终输出。
通过上述方法构建 Maxout 网络,实现 Mnist 分类。
在神经网络中使用 softmax 计算 loss 时对于初学者常常会范很多错误,下面通过具体的实
例代码演示需要注意哪些关键的地方与具体的用法。
6.5.1 实例 22 交叉熵实验
对于交叉熵这个比较生僻的术语,在深度学习领域中是最常见不过了,由于其常用性,在
TensorFlow 中会被封装成为多个版本, 有的公式里直接带了交叉熵,有的需要自己单独求一下
交叉熵,而在构建模型时,如果这块知识不扎实,出现问题时很难分析是模型的问题还是交叉熵
的使用问题。 这里有必要通过几个小实验将其弄得更明白一些。
案例描述
下面一段代码,假设有一个标签 labels 和一个网络输出值 logits。
这个案例就是以这两个值来进行以下 3 次实验:
(1)两次 softmax 实验:将输出值 logits 分别进行 1 次和 2 次 softmax,观察两次的区别
及意义;
(2)观察交叉熵:将上个步骤中的两个值分别进行 softmax_cross_entropy_with_logits,
观察区别;
(3)自建公式实验:将做两次 softmax 的值放到自建组合的公式里得到正确的值。
代码 6-1 softmax 应用

运行上面代码输出结果如下:

可以看到: logits 里面的值原本加和都是大于 1 的,但是经过 softmax 之后,总和变成了 1。
样本中第一个是跟标签分类相符的,第二与标签分类不符,所以第一个的交叉熵比较小为
0.02215516,而第二个比较大 3.09967351。
下面开始验证下前面说所的实验:
● 比较 scaled 和 scaled2 可以看到:经过第二次的 softmax 后,分布概率会有变化,而
scaled 才是我们真实转化的 softmax 值。
● 比较 rel1 和 rel2 可以看到:传入 softmax_cross_entropy_with_logits 的 logits 是
不 需 要 进 行 softmax 的 。 如 果 将 softmax 后 的 值 scaled 传 入softmax_cross_entropy_with_logits 就相当于进行了两次的 softmax 转换。
对于已经用 softmax 转换过的 scaled,在计算 loss 时就不能在用 TensorFlow 里面的softmax_cross_entropy_with_logits 了。读者可以自己写一个 loss 的函数,参见 rel3 的生成,通过自己组合的函数实现了 softmax_cross_entropy_with_logits 一样的结果。
6.5.2实例 23:one_hot 实验
其实输入的标签也可以不是标准的 one-hot, 下面用一组总和也为 1 但是每个都不等于 0 或1 的数组来代替标签,看看效果。
案例描述
对非 one-hot 编码为标签的数据进行交叉熵的计算,比较其与 one-hot 编码的交熵之间的差别。
接上述代码,将标签换为[[0.4,0.1,0.5],[0.3,0.6,0.1]]与原始的[[0,0,1], [0,1,0]]代
表的分类意义等价,将这个标签代入交叉熵。
代码 6-1 softmax 应用(续)

运行上面代码,生成如下结果:
比较前面的 rel1 发现,对于正确分类的交叉熵和错误分类的交叉熵,二者的结果差别没有
标准 one-hot 那么明显。
6.5.3 实例 24: sparse 交叉熵使用
下面再举个例子看一下 sparse_softmax_cross_entropy_with_logits 的用法,它需要使用
非 one-hot 的标签。所以,要把前面的标签换成具体数值[2,1],具体代码如下。
案例描述
演示使用 sparse_softmax_cross_entropy_with_logits 函数,对非 one-hot 的标签进行交
叉熵计算,比较其与 one-hot 标签在使用上的区别。
代码 6-1 softmax 应用(续)
运行上面代码,生成如下结果:发现 rel5 与前面的 rel1 结果完全一样。
6.5.4 实例 25:计算 loss 值
在真正的神经网络中,得到这样的一个数组并不能满足要求,还需要对其求均值,使其最终
变成一个具体的数值,如下代码。
案例描述
演示通过分别对上文交叉熵结果 result1 与 softmax 后的结果 logits_scaled 计算 loss,
验证如下结论:
(1)对于 softmax_cross_entropy_with_logits 后的结果求 loss 直接取均值;
(2)对于 softmax 后的结果使用-tf.reduce_sum(labels * tf.log(logits_scaled))求 loss。
(3)对于 softmax 后的结果使用-tf.reduce_sum(labels*tf.log(logits_scaled),1)等同于
softmax_cross_entropy_with_logits 结果。
(4)由 1 和 3 可以推出对 3 进行求均值也可以得出正确的 loss 值,合并起来的公式为:
tf.reduce_sum(-tf.reduce_sum(labels*tf.log(logits_scaled),1)) =loss(该结论是由前
面的验证推导出来,有兴趣的读者可以自行验证)
代码 6-1 softmax 应用(续)
运行上面的代码,生成如下结果:这便是我们最终要得到的损失值了。
而对于已经 rel3 这种已经求得 softmax 的情况求 loss,可以把公式进一步简化成
![]()
接着添加示例代码。
代码 6-1 softmax 应用(续)运行上面代码输出结果如下:
与 loss 的值完全吻合。
6.6.4 实例 26:退化学习率的用法举例
本例子主要是演示学习率衰减的使用方法。
例子中使用了迭代循环计数变量 global_step 来标记循环次数,初始学习率为 0.1,令其以
每 10 次衰减 0.9 的速度来进行退化。
案例描述
定义一个学习率变量,将其衰减系数设置好,并设置好迭代循环的次数,将每次迭代运算的
次数与学习率打印出来,观察学习率按照次数退化的现象。
代码 6-3 退化学习率
上面代码运行如下:第一个数是迭代的次数,第二个输出是学习率。可以看到学习率在逐渐变小。在第 11 次由原来的 0.1 变到了 0.09。
注意:这是一种常用的训练策略,在训练神经网络时,通常在训练刚开始时使用较大的learning rate,随着训练的进行,会慢慢的减小 learning rate。在使用过程时,一定要把当前迭代次数 global_step 传进去,不然不会有退化的功能。6.8.2 实例 27:用 Maxout 网络实现 Mnist 分类
本例子主要是演示 Maxout 网络的构建方法。
例 子 中 , 拿 6.5 节 的 练习 题 答 案 来 修 改 代 码 ,在 本 书 附 带 资 源 中 的 “ 代 码 6-2sparesoftmaxwithminist.py” 里面做如下改动。
案例描述
Maxout 网络的构建方法:通过 reduce_max 函数对多个神经元的输出来计算 Max 值,将 Max
值通过另一套学习参数计算得到最终输出。
通过上述方法构建 Maxout 网络,实现 Mnist 分类。
代码 6-4 Maxout 网络实现 mnist 分类
在网络模型部分,添加一层 maxout,然后将 Maxout 作为 maxsoft 的交叉熵输入。学习率设
为 0.04,迭代次数设为 200。运行代码,得到如下结果:
 可以看到损失值下降到 0.28,随着迭代的次数增加,还会继续下降。有兴趣的读者可以自己接着优化。
可以看到损失值下降到 0.28,随着迭代的次数增加,还会继续下降。有兴趣的读者可以自己接着优化。
Maxout 的拟合功能很强大,但是也会有节点过多,参数过多,训练过慢的缺点。在下一章中,我们还会学习一种类似与 maxout 的全连接网络。到时会更深刻的讨论拟合的方法及意义。
更多章节请购买《深入学习之 TensorFlow 入门、原理与进阶实战》全本