The Pairing-Based Cryptography Library的学习

这个库由stanford大学开发，库的地址为http://crypto.stanford.edu/pbc/。

总介绍：

1，功能足够的丰富：

The PBC library is designed to be the backbone of implementations of pairing-based cryptosystems, thus speed and portability are important goals. It provides routines such as elliptic curve generation, elliptic curve arithmetic and pairing computation.

2，接口足够的抽象：

The API is abstract enough that the PBC library can be used even if the programmer possesses only an elementary understanding of pairings. There is no need to learn about elliptic curves or much of number theory. (The minimum requirement is some knowledge of cyclic groups and properties of the pairing.)

安装：

1，如果直接按其教程安装./configure会提示缺少一些东西：

tatostar@junjieshi:~/G2/Waters Encryption/pbc-0.5.14$ sudo ./configure
checking for a BSD-compatible install... /usr/bin/install -c
checking whether build environment is sane... yes
checking for a thread-safe mkdir -p... /bin/mkdir -p
checking for gawk... no
checking for mawk... mawk
checking whether make sets $(MAKE)... yes
configure: WARNING: Libtool does not cope well with whitespace in `pwd`
checking build system type... x86_64-unknown-linux-gnu
checking host system type... x86_64-unknown-linux-gnu
checking how to print strings... printf
checking for style of include used by make... GNU
checking for gcc... gcc
checking whether the C compiler works... yes
checking for C compiler default output file name... a.out
checking for suffix of executables... 
checking whether we are cross compiling... no
checking for suffix of object files... o
checking whether we are using the GNU C compiler... yes
checking whether gcc accepts -g... yes
checking for gcc option to accept ISO C89... none needed
checking dependency style of gcc... gcc3
checking for a sed that does not truncate output... /bin/sed
checking for grep that handles long lines and -e... /bin/grep
checking for egrep... /bin/grep -E
checking for fgrep... /bin/grep -F
checking for ld used by gcc... /usr/bin/ld
checking if the linker (/usr/bin/ld) is GNU ld... yes
checking for BSD- or MS-compatible name lister (nm)... /usr/bin/nm -B
checking the name lister (/usr/bin/nm -B) interface... BSD nm
checking whether ln -s works... yes
checking the maximum length of command line arguments... 1572864
checking whether the shell understands some XSI constructs... yes
checking whether the shell understands "+="... yes
checking how to convert x86_64-unknown-linux-gnu file names to x86_64-unknown-linux-gnu format... func_convert_file_noop
checking how to convert x86_64-unknown-linux-gnu file names to toolchain format... func_convert_file_noop
checking for /usr/bin/ld option to reload object files... -r
checking for objdump... objdump
checking how to recognize dependent libraries... pass_all
checking for dlltool... no
checking how to associate runtime and link libraries... printf %s\n
checking for ar... ar
checking for archiver @FILE support... @
checking for strip... strip
checking for ranlib... ranlib
checking command to parse /usr/bin/nm -B output from gcc object... ok
checking for sysroot... no
checking for mt... mt
checking if mt is a manifest tool... no
checking how to run the C preprocessor... gcc -E
checking for ANSI C header files... yes
checking for sys/types.h... yes
checking for sys/stat.h... yes
checking for stdlib.h... yes
checking for string.h... yes
checking for memory.h... yes
checking for strings.h... yes
checking for inttypes.h... yes
checking for stdint.h... yes
checking for unistd.h... yes
checking for dlfcn.h... yes
checking for objdir... .libs
checking if gcc supports -fno-rtti -fno-exceptions... no
checking for gcc option to produce PIC... -fPIC -DPIC
checking if gcc PIC flag -fPIC -DPIC works... yes
checking if gcc static flag -static works... yes
checking if gcc supports -c -o file.o... yes
checking if gcc supports -c -o file.o... (cached) yes
checking whether the gcc linker (/usr/bin/ld -m elf_x86_64) supports shared libraries... yes
checking whether -lc should be explicitly linked in... no
checking dynamic linker characteristics... GNU/Linux ld.so
checking how to hardcode library paths into programs... immediate
checking whether stripping libraries is possible... yes
checking if libtool supports shared libraries... yes
checking whether to build shared libraries... yes
checking whether to build static libraries... yes
checking for gcc... (cached) gcc
checking whether we are using the GNU C compiler... (cached) yes
checking whether gcc accepts -g... (cached) yes
checking for gcc option to accept ISO C89... (cached) none needed
checking dependency style of gcc... (cached) gcc3
checking whether gcc and cc understand -c and -o together... yes
checking how to run the C preprocessor... gcc -E
checking whether ln -s works... yes
checking whether make sets $(MAKE)... (cached) yes
checking for flex... no
checking for lex... no
************************
flex not found
************************

2，我们按照提示分别下载安装这些就好了：

tatostar@junjieshi:~/G2/Waters Encryption/pbc-0.5.14$ sudo apt-get install flex

tatostar@junjieshi:~/G2/Waters Encryption/pbc-0.5.14$ sudo apt-get install bison byacc

************************
gmp library not found
add its path to LDFLAGS
see ./configure --help
************************

3，由于PBC是基于GMP开发的，根据提示我们需要先安装GMP：从https://gmplib.org/下载gmp-5.1.3.tar.bz2

GNU MP is a portable library written in C for arbitrary precision arithmetic on integers, rational numbers, and floating-point numbers. It aims to provide the fastest possible arithmetic for all applications that need higher precision than is directly supported by the basic C types.

按要求：

• tatostar@junjieshi:~/G2/Waters Encryption/gmp-5.1.3$ sudo ./configure 
• 最终得到：configure: summary of build options:
  
  
    Version:           GNU MP 5.1.3
    Host type:         coreisbr-unknown-linux-gnu
    ABI:               64
    Install prefix:    /usr/local
    Compiler:          gcc -std=gnu99
    Static libraries:  yes
    Shared libraries:  yes
• tatostar@junjieshi:~/G2/Waters Encryption/gmp-5.1.3$ make install
  
• 最终得到：make[2]: Leaving directory `/home/tatostar/G2/Waters Encryption/gmp-5.1.3'
  make[1]: Leaving directory `/home/tatostar/G2/Waters Encryption/gmp-5.1.3'
• Libraries have been installed in:
     /usr/local/lib
  
  
  If you ever happen to want to link against installed libraries
  in a given directory, LIBDIR, you must either use libtool, and
  specify the full pathname of the library, or use the `-LLIBDIR'
  flag during linking and do at least one of the following:
     - add LIBDIR to the `LD_LIBRARY_PATH' environment variable
       during execution
     - add LIBDIR to the `LD_RUN_PATH' environment variable
       during linking
     - use the `-Wl,-rpath -Wl,LIBDIR' linker flag
     - have your system administrator add LIBDIR to `/etc/ld.so.conf'
  
  
  See any operating system documentation about shared libraries for
  more information, such as the ld(1) and ld.so(8) manual pages.
  ----------------------------------------------------------------------
   /bin/mkdir -p '/usr/local/include'
   /usr/bin/install -c -m 644 gmp.h '/usr/local/include'
  make  install-data-hook
  make[4]: Entering directory `/home/tatostar/G2/Waters_Encryption/gmp-5.1.3'
  
  
  +-------------------------------------------------------------+
  | CAUTION:                                                    |
  |                                                             |
  | If you have not already run "make check", then we strongly  |
  | recommend you do so.                                        |
  |                                                             |
  | GMP has been carefully tested by its authors, but compilers |
  | are all too often released with serious bugs.  GMP tends to |
  | explore interesting corners in compilers and has hit bugs   |
  | on quite a few occasions.                                   |
  |                                                             |
  +-------------------------------------------------------------+
• 虽然make check会报一些错，但我们接下来会看到这并不影响PBC的安装。

4，再次tatostar@junjieshi:~/G2/Waters_Encryption/pbc-0.5.14$ sudo ./configure 

checking whether make sets $(MAKE)... (cached) yes
checking for flex... flex
checking lex output file root... lex.yy
checking lex library... -lfl
checking whether yytext is a pointer... yes
checking for bison... bison -y
checking for pow in -lm... yes
checking for __gmpz_init in -lgmp... yes
checking for size_t... yes
checking for working alloca.h... yes
checking for alloca... yes
checking for ANSI C header files... (cached) yes
checking for stdlib.h... (cached) yes
checking for string.h... (cached) yes
checking sys/time.h usability... yes
checking sys/time.h presence... yes
checking for sys/time.h... yes
checking for an ANSI C-conforming const... yes
checking for inline... inline
checking for size_t... (cached) yes
checking whether time.h and sys/time.h may both be included... yes
checking for stdlib.h... (cached) yes
checking for GNU libc compatible malloc... yes
checking for stdlib.h... (cached) yes
checking for GNU libc compatible realloc... yes
checking for floor... no
checking for gettimeofday... yes
checking for memmove... yes
checking for memset... yes
checking for pow... no
checking for sqrt... no
checking for strchr... yes
checking for strdup... yes
configure: creating ./config.status
config.status: creating Makefile
config.status: creating example/Makefile
config.status: creating gen/Makefile
config.status: creating config.h
config.status: executing depfiles commands
config.status: executing libtool commands


global build variables
-----------------------------------------
Wed Dec 4 10:55:21 CST 2013
host info:        x86_64-unknown-linux-gnu
optimized build:  no
compiler (CC):    gcc
LDFLAGS:          
CPPFLAGS:         
CFLAGS:            -Wall -W -Wfloat-equal -Wpointer-arith -Wcast-align -Wstrict-prototypes -Wredundant-decls -Wendif-labels -Wshadow -pipe -ffast-math -U__STRICT_ANSI__ -std=gnu99 -fomit-frame-pointer -O3
LEX:              flex
AM_LFLAGS:        
LFLAGS:           
YACC:             bison -y
AM_YFLAGS:        
YFLAGS:           
-----------------------------------------

接下来我们来测试一下是否已经安装成功：

从这些示例中我们可以看出，默认情况下，系统已经设定好了pairing的一些参数，包括G1、G2以及它们的order、generator等。

关于这个小解释程序的一些介绍可以参见http://crypto.stanford.edu/pbc/manual/ch07s01.html。

Initially, the variables G1, G2, GT and Zr are represent groups associated with a particular A pairing.

Assignments such as variable := expression; return the value of the variable.

The arithmetic operators +, -, /, *, ^ have the standard precedence. The C comparison operators and ternary operator are available.

Each statement should be terminated by a semicolon.

//****************************************************************SEPARATION LINE***********************************************************************************\\

具体使用

（manual笔记）

由于我们最终需要的十一个bilinear map e，之前首先想到的是Dan boneh使用的weil pairing。但似乎一直没有直接的在这个library中找到显式说是weil pairing的函数。但有一个例子是介绍BLS signature的，看原始的论文，好像其使用的pairing就是weil pairing或者实现中的Tate pairing。

Programs using the PBC library should include the file pbc.h:

#include 

and linked against the PBC library and the GMP library, e.g.

$ gcc program.c -L. -lpbc -lgmp

PBC follows GMP in several respects:

• Output arguments generally precede input arguments.
• The same variable can be used as input and output in one call.
• Before a variable may be used it must be initialized exactly once. When no longer needed it must be cleared. For efficiency, unnecessary initializating and clearing should be avoided.
• PBC variables ending with _t behave the same as GMP variables in function calls: effectively as call-by references. In other words, as in GMP, if a function that modifies an input variable, that variable remains modified when control return is returned to the caller.
• Like GMP, variables automatically allocate memory when needed. By default, malloc() and friends are called but this can be changed.
• PBC functions are mostly reentrant.

In contrast, PBC uses the element_t data type for elements of different algebraic structures, such as elliptic curve groups, polynomial rings and finite fields. Functions assume their inputs come from appropriate algebraic structures.

PBC data types and functions can be categorized as follows. The first two alone suffice for a range of applications.

• element_t: elements of an algebraic structure.
• pairing_t: pairings where elements belong; can initialize from sample pairing parameters bundled with PBC in the param subdirectory.
• pbc_param_t: used to generate pairing parameters.
• pbc_cm_t: parameters for constructing curves via the CM method; sometimes required by pbc_param_t.
• field_t: algebraic structures: groups, rings and fields; used internally by pairing_t.
• a few miscellaneous functions, such as ones controlling how random bits are generated.

Tutorial：

BLS signatures

First we include pbc/pbc.h:

#include 

Next we initialize a pairing:

pairing_t pairing;
char param[1024];
size_t count = fread(param, 1, 1024, stdin);
if (!count) pbc_die("input error");
pairing_init_set_buf(pairing, param, count);

Later we give pairing parameters to our program on standard input. Any file in the param subdirectory will suffice, for example:

$ bls < param/a.param

We shall need several element_t variables to hold the system parameters, keys and other quantities. We declare them and initialize them,

element_t g, h;
element_t public_key, secret_key;
element_t sig;
element_t temp1, temp2;

element_init_G2(g, pairing);
element_init_G2(public_key, pairing);
element_init_G1(h, pairing);
element_init_G1(sig, pairing);
element_init_GT(temp1, pairing);
element_init_GT(temp2, pairing);
element_init_Zr(secret_key, pairing);

（以上几步感觉主要目的是声明各个变量所在的group/field，以明确接下来的modular arithmetic。如

element_init_G2(public_key, pairing);

应该是声明public_key是G2中的元素，而G2是由pairing所规定的。

generate system parameters,

element_random(g);

generate a private key,

element_random(secret_key);

and the corresponding public key.

element_pow_zn(public_key, g, secret_key);

When given a message to sign, we first compute its hash, using some standard hash algorithm. Many libraries can do this, and this operation does not involve pairings, so PBC does not provide functions for this step. For this example, and our message has already been hashed, possibly using another library.

Say the message hash is "ABCDEF" (a 48-bit hash). We map these bytes to an element h of G1,

element_from_hash(h, "ABCDEF", 6);

then sign it:

element_pow_zn(sig, h, secret_key);

To verify this signature, we compare the outputs of the pairing applied to the signature and system parameter, and the pairing applied to the message hash and public key. If the pairing outputs match then the signature is valid.

pairing_apply(temp1, sig, g, pairing);
pairing_apply(temp2, h, public_key, pairing);
if (!element_cmp(temp1, temp2)) {
    printf("signature verifies\n");
} else {
    printf("signature does not verify\n");
}

 这里

pairing_apply(temp1, sig, g, pairing);

是指使用map 得到temp1 = e(sig,g);

Chapter 3. Pairing functions

An application should first initialize a pairing object. This causes PBC to setup curves, groups and other mathematical miscellany. After that, elements can be initialized and manipulated for cryptographic operations.

Parameters for various pairings are included with the PBC library distribution in the param subdirectory, and some are suitable for cryptographic use. Some programs in the gen subdirectory may be used to generate parameters

Pairings involve three groups of prime order. The PBC library calls them G1, G2, and GT, and calls the order r. The pairing is a bilinear map that takes two elements as input, one from G1 and one from G2, and outputs an element of GT.

The elements of G2 are at least as long as G1; G1 is guaranteed to be the shorter of the two. Sometimes G1 and G2 are the same group (i.e. the pairing is symmetric) so their elements can be mixed freely. In this case the pairing_is_symmetric function returns 1.

Bilinear pairings are stored in the data type pairing_t. Functions that operate on them start with pairing_.

Initializing pairings

To initialize a pairing from an ASCIIZ string:

pairing_t pairing;
pairing_init_set_str(pairing, s);  // Where s is a char *.

The string s holds pairing parameters in a text format. The param subdirectory contains several examples.

Alternatively, call:

pairing_t pairing;
pairing_init_pbc_param(pairing, param);

where param is an initialized pbc_param_t

int pairing_init_set_str(pairing_t pairing, const char *s)

Initialize pairing from parameters in a ASCIIZ string str Returns 0 on success, 1 on failure.

int pairing_init_set_buf(pairing_t pairing, const char *s, size_t len)

Same, but read at most len bytes. If len is 0, it behaves as the previous function. Returns 0 on success, 1 on failure.

void pairing_init_pbc_param(struct pairing_s *pairing, pbc_param_t p)

Initialize a pairing with pairing parameters p.

void pairing_clear(pairing_t pairing)

Free the space occupied by pairing. Call whenever a pairing_t variable is no longer needed. Only call this after all elements associated with pairing have been cleared, as they need information stored in the pairing structure.

Applying pairings

The function pairing_apply can be called to apply a bilinear map.The order of the inputs is important. The first, which holds the output, must be from the group GT. The second must be from G1, the third from G2, and the fourth must be the pairing_t variable that relates them.

In some applications, the programmer may know that many pairings with the same G1 input will be computed. If so, preprocessing should be used to avoid repeating many calculations saving time in the long run. A variable of type pairing_pp_t should be declared, initialized with the fixed G1 element, and then used to compute pairings:

pairing_pp_t pp;
pairing_pp_init(pp, x, pairing); // x is some element of G1
pairing_pp_apply(r1, y1, pp); // r1 = e(x, y1)
pairing_pp_apply(r2, y2, pp); // r2 = e(x, y2)
pairing_pp_clear(pp); // don't need pp anymore

Never mix and match G1, G2, and GT groups from different pairings.

void pairing_pp_init(pairing_pp_t p, element_t in1, pairing_t pairing)

Get ready to perform a pairing whose first input is in1, and store the results of time-saving precomputation in p.

void pairing_pp_clear(pairing_pp_t p)

Clear p. This should be called after p is no longer needed.

void pairing_pp_apply(element_t out, element_tin2, pairing_pp_t p)

Compute a pairing using in2 and the preprocessed information stored in p and store the output in out.The inputs to the pairing are the element previously used to initialize p and the element in2.

void element_pairing(element_t out, element_t in1, element_t in2)

Computes a pairing: out = e(in1, in2), where in1, in2, out must be in the groups G1, G2, GT.

这几个元素需要已经初始声明过了。

void element_prod_pairing(element_t out, element_t in1[], element_t in2[], int n)

Computes the product of pairings, that is out = e(in1[0], in2[0]) … e(in1[n-1], in2[n-1]). The arrays in1, in2 must have at least n elements belonging to the groups G1, G2 respectively, and out must belong to the group GT.

Other pairing functions

介绍一些获取pairing参数的函数：

int pairing_is_symmetric(pairing_t pairing)

Returns true if G1 and G2 are the same group.

int pairing_length_in_bytes_G1(pairing_t pairing)

Returns the length in bytes needed to represent an element of G1.

int pairing_length_in_bytes_x_only_G1(pairing_t pairing)

Returns the length in bytes needed to represent the x-coordinate of an element of G1.

int pairing_length_in_bytes_compressed_G1(pairing_t pairing)

Returns the length in bytes needed to represent a compressed form of an element of G1. There is some overhead in decompressing.

int pairing_length_in_bytes_G2(pairing_t pairing)

Returns the length in bytes needed to represent an element of G2.

int pairing_length_in_bytes_compressed_G2(pairing_t pairing)

Returns the length in bytes needed to represent a compressed form of an element of G2. There is some overhead in decompressing.

int pairing_length_in_bytes_x_only_G2(pairing_t pairing)

Returns the length in bytes needed to represent the x-coordinate of an element of G2.

int pairing_length_in_bytes_GT(pairing_t pairing)

Returns the length in bytes needed to represent an element of GT.

int pairing_length_in_bytes_Zr(pairing_t pairing)

Returns the length in bytes needed to represent an element of Zr.

Chapter 4. Element functions

Elements of groups, rings and fields are stored in the element_t data type. Variables of this type must be initialized before use, and should be cleared after they are no longer needed.

The element_ functions must be used with caution. Just as division by zero does not make sense for integers, some operations may not make sense for particular elements. For example, in a ring, one cannot in general invert elements.

Another caveat is that many of these functions assume their arguments come from the same ring, group or field. No implicit type casting is performed.

For debug builds, turn on run-time checks by defining PBC_DEBUG before including pbc.h:

#define PBC_DEBUG
#include 

Also, when PBC_DEBUG is defined, the following macros are active. Normally they are replaced with empty statements.

PBC_ASSERT(expr, msg)

Macro: if expr evaluates to 0, print msg and exit.

PBC_ASSERT_MATCH2(a, b)

Macro: if elements a and b are from different fields then exit.

PBC_ASSERT_MATCH3(a, b, c)

Macro: if elements a, b and c are from different fields then exit.

Initializing elements

When an element is initialized it is associated with an algebraic structure, such as a particular finite field or elliptic curve group.

We use G1 and G2 to denote the input groups to the pairing, and GT for the output group. All have order r, and Zr means the ring of integers modulo r. G1 is the smaller group (the group of points over the base field). With symmetric pairings, G1 = G2.

void element_init_G1(element_t e, pairing_t pairing)

void element_init_G2(element_t e, pairing_t pairing)

void element_init_GT(element_t e, pairing_t pairing)

Initialize e to be an element of the group G1, G2 or GT of pairing.

void element_init_Zr(element_t e, pairing_t pairing)

Initialize e to be an element of the ring Z_r of pairing. r is the order of the groups G1, G2 and GT that are involved in the pairing.

void element_init_same_as(element_t e, element_t e2)

Initialize e to be an element of the algebraic structure that e2 lies in.

void element_clear(element_t e)

Free the space occupied by e. Call this when the variable e is no longer needed.

Assigning elements

These functions assign values to elements. When integers are assigned, they are mapped to algebraic structures canonically if it makes sense (e.g. rings and fields).

void element_set0(element_t e)

Set e to zero.

void element_set1(element_t e)

Set e to one.

void element_set_si(element_t e, signed long int i)

Set e to i.

void element_set_mpz(element_t e, mpz_t z)

Set e to z.

void element_set(element_t e, element_t a)

Set e to a.

Converting elements

void element_to_mpz(mpz_t z, element_t e)

Converts e to a GMP integer z if such an operation makes sense

void element_from_hash(element_t e, void *data, int len)

Generate an element e deterministically from the len bytes stored in the buffer data.

Element arithmetic

Unless otherwise stated,all element_t arguments to these functions must have been initialized to be from the same algebraic structure. When one of these functions expects its arguments to be from particular algebraic structures, this is reflected in the name of the function.

The addition and multiplication functions perform addition and multiplication operations in rings and fields. For groups of points on an ellitpic curve, such as the G1 and G2 groups associated with pairings, both addition and multiplication represent the group operation (and similarly both 0 and 1 represent the identity element). It is recommended that programs choose and one convention and stick with it to avoid confusion.

In contrast, the GT group is currently implemented as a subgroup of a finite field, so only multiplicative operations should be used for GT.

void element_add(element_t n, element_t a, element_t b)

Set n to a + b.

void element_sub(element_t n, element_t a, element_t b)

Set n to a - b.

void element_mul(element_t n, element_t a, element_t b)

Set n = a b.

void element_mul_mpz(element_t n, element_t a, mpz_t z)

void element_mul_si(element_t n, element_t a, signed long int z)

Set n = a z, that is a + a + … + a where there are z a's.

void element_mul_zn(element_t c, element_t a, element_t z)

z must be an element of a integer mod ring (i.e. Z_n for some n). Set c = a z, that is a + a + … + a where there are z a's.

void element_div(element_t n, element_t a, element_t b)

Set n = a / b.

void element_double(element_t n, element_t a)

Set n = a + a.

void element_halve(element_t n, element_t a)

Set n = a/2

void element_square(element_t n, element_t a)

Set n = a²

void element_neg(element_t n, element_t a)

Set n = -a.

void element_invert(element_t n, element_t a)

Set n to the inverse of a.

Exponentiating elements

Exponentiation and multiexponentiation functions. If it is known in advance that a particular element will be exponentiated several times in the future, time can be saved in the long run by first calling the preprocessing function:

element_pp_t g_pp;
element_pp_init(g_pp, g);
element_pp_pow(h, pow1, g_pp); // h = g^pow1
element_pp_pow(h, pow2, g_pp); // h = g^pow2
element_pp_pow(h, pow3, g_pp); // h = g^pow3
element_pp_clear(g_pp);

void element_pow_mpz(element_t x, element_t a, mpz_t n)

Set x = aⁿ, that is a times a times … times a where there are n a's.

void element_pow_zn(element_t x, element_t a, element_t n)

Set x = aⁿ, where n is an element of a ring Z_N for some N (typically the order of the algebraic structure x lies in).

void element_pow2_mpz(element_t x, element_t a1, mpz_t n1, element_t a2, mpz_t n2)

Sets x = a1ⁿ¹ a2ⁿ², and is generally faster than performing two separate exponentiations.

void element_pow2_zn(element_t x, element_t a1, element_t n1, element_t a2, element_t n2)

Also sets x = a1ⁿ¹ a2ⁿ², but n1, n2 must be elements of a ring Z_n for some integer n.

void element_pow3_mpz(element_t x, element_t a1, mpz_t n1, element_t a2, mpz_t n2, element_t a3, mpz_t n3)

Sets x = a1ⁿ¹ a2ⁿ² a3ⁿ³, generally faster than performing three separate exponentiations.

void element_pow3_zn(element_t x, element_t a1, element_t n1, element_t a2, element_t n2, element_t a3, element_t n3)

Also sets x = a1ⁿ¹ a2ⁿ² a3ⁿ³, but n1, n2, n3 must be elements of a ring Z_n for some integer n.

void element_pp_init(element_pp_t p, element_t in)

Prepare to exponentiate an element in, and store preprocessing information in p.

void element_pp_clear(element_pp_t p)

Clear p. Should be called after p is no longer needed.

void element_pp_pow(element_t out, mpz_t power, element_pp_t p)

Raise in to power and store the result in out, where in is a previously preprocessed element, that is, the second argument passed to a previous element_pp_init call.

void element_pp_pow_zn(element_t out, element_t power, element_pp_t p)

Same except power is an element of Z_n for some integer n.

void element_dlog_brute_force(element_t x, element_t g, element_t h)

Computes x such that g^x = h by brute force, where x lies in a field where element_set_mpz() makes sense.

void element_dlog_pollard_rho(element_t x, element_t g, element_t h)

Computes x such that g^x = h using Pollard rho method, where x lies in a field where element_set_mpz() makes sense.

Comparing elements

These functions compare elements from the same algebraic structure.

int element_is1(element_t n)

Returns true if n is 1.

int element_is0(element_t n)

Returns true if n is 0.

int element_cmp(element_t a, element_t b)

Returns 0 if a and b are the same, nonzero otherwise.

int element_is_sqr(element_t a)

Returns nonzero if a is a perfect square (quadratic residue), zero otherwise.

int element_sgn(element_t a)

int element_sign(element_t a)

If a is zero, returns 0. For nozero a the behaviour depends on the algebraic structure, but has the property that element_sgn(a) = -element_sgn(-a) and element_sgn(a) = 0 implies a = 0 with overwhelming probability.

Element I/O

Functions for producing human-readable outputs for elements. Converting elements to and from bytes are discussed later.

略

Random elements

Only works for finite algebraic structures. Effect on polynomial rings, fields of characteristic zero, etc. undefined.

See the section called “Random bits” for how PBC gets random bits.

void element_random(element_t e)

If the e lies in a finite algebraic structure, assigns a uniformly random element to e.

Element import/export

Functions for serializing and deserializing elements.

略

Chapter 5. Param functions

Pairings are initialized from pairing parameters, which are objects of type pbc_param_t. Some applications can ignore this data type because pairing_init_set_str() handles it behind the scenes: it reads a string as a pbc_param_t, then initializes a pairing with these parameters.

int pbc_param_init_set_str(pbc_param_t par, const char *s)

Initializes pairing parameters from the string s. Returns 0 if successful, 1 otherwise.

int pbc_param_init_set_buf(pbc_param_t par, const char *s, size_t len)

Same, but read at most len bytes. If len is 0, it behaves as the previous function. Returns 0 if successful, 1 otherwise.

void pbc_param_out_str(FILE *stream, pbc_param_t p)

Write pairing parameters to 'stream' in a text format.

void pbc_param_clear(pbc_param_t p)

Clear p. Call after p is no longer needed.

Param generation

These were used to prepare the sample parameters in the param subdirectory.

We label the pairing families with capital letters roughly in the order of discovery, so we can refer to them easily. Type A is fastest. Type D is a good choice when elements should be short but is slower. Type F has even shorter elements but is slower still. The speed differences are hardware-dependent, and also change when preprocessing is used. Type B and C are unimplemented.

void pbc_param_init_a_gen(pbc_param_t par, int rbits, int qbits)

Generate type A pairing parameters and store them in p, where the group order r is rbits long, and the order of the base field q is qbits long. Elements take qbits to represent.

To be secure, generic discrete log algorithms must be infeasible in groups of order r, and finite field discrete log algorithms must be infeasible in finite fields of order q^2, e.g. rbits = 160, qbits = 512.

The file param/a.param contains parameters for a type A pairing suitable for cryptographic use.

略

//*******************************************************************SELF-TRY*********************************************************************************//

在我自己写程序时仍然发生了一些anonying的小错误，让人抓狂！

这里要非常非常感激于http://www.network-theory.co.uk/docs/gccintro/gccintro_25.html中的相关介绍！

经过以上步骤后查看系统的路径可以发现：

tatostar@junjieshi:/usr/local/lib$ ls
libgmp.a   libgmp.so.10      libpbc.la    libpbc.so.1.0.0  python3.3
libgmp.la  libgmp.so.10.1.3  libpbc.so    ocaml            site_ruby
libgmp.so  libpbc.a          libpbc.so.1  python2.7

tatostar@junjieshi:/usr/local/include$ ls
gmp.h  pbc
tatostar@junjieshi:/usr/local/include$ cd pbc
tatostar@junjieshi:/usr/local/include/pbc$ ls
pbc_a1_param.h        pbc_g_param.h  pbc_poly.h
pbc_a_param.h         pbc.h          pbc_random.h
pbc_curve.h           pbc_hilbert.h  pbc_singular.h
pbc_d_param.h         pbc_i_param.h  pbc_ternary_extension_field.h
pbc_e_param.h         pbc_memory.h   pbc_test.h
pbc_field.h           pbc_mnt.h      pbc_utils.h
pbc_fieldquadratic.h  pbc_multiz.h   pbc_z.h
pbc_f_param.h         pbc_pairing.h
pbc_fp.h              pbc_param.h

这说明已经将static library以及dynamic library都安装好了。

gcc -Wall test1.c -lpbc -lgmp
test1.c:1:17: fatal error: pbc.h: No such file or directory
compilation terminated.

改为：

tatostar@junjieshi:~/G2/WE_IBE/pbc-0.5.14/Mytest$ gcc -Wall test1.c -o test1 -I/usr/local/include/pbc -lpbc -lgmp
tatostar@junjieshi:~/G2/WE_IBE/pbc-0.5.14/Mytest$ ls
a.out  test1  test1.c

可以编译通过了。

运行:

tatostar@junjieshi:~/G2/WE_IBE/pbc-0.5.14/Mytest$ ./test1 <../param/a.param 
./test1: error while loading shared libraries: libpbc.so.1: cannot open shared object file: No such file or directory

说明加载动态库出错了！

之后根据上面链接中的介绍，尝试了下：

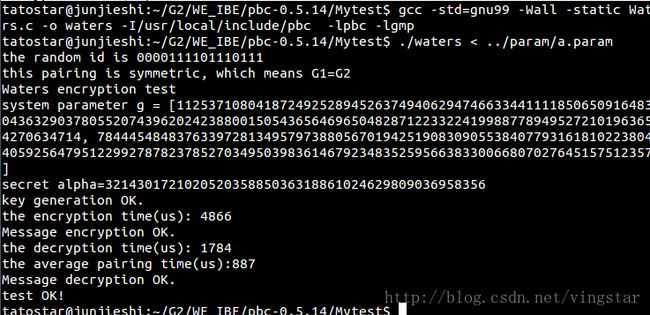
 gcc -Wall -static bls.c -o test2 -I/usr/local/include/pbc -L/usr/local/lib -lpbc -lgmp
tatostar@junjieshi:~/G2/WE_IBE/pbc-0.5.14/Mytest$ ls
a.out  bls.c  test1  test1.c  test2
tatostar@junjieshi:~/G2/WE_IBE/pbc-0.5.14/Mytest$ ./test2 <../param/a.param 
Short signature test
system parameter g = [4676687947331153055357403980767031900270664796822484224813019288191758362617147147155195650911270953880240621696314307705682735511703723548485451565379669, 2774220716150738737020236538584880183761685986848874306878606440044265716168219282854783540334545068812684350699006007806856414026197021013139013035504805]

成功了！！

IBE:

Setup:

设n=16

summary:

1,借助于open source的PBC（Pairing Based Cryptography）library（http://crypto.stanford.edu/pbc）实现其中的binear map的 pairing操作。

具体而言使用了Type A pairing，这种是“Fastest pairing, good for cryptosystems where group element size is not critical. Uses supersingular curve Y^2 = X^3 + X. Group order is a Solinas prime.” 

没有考虑具体通过怎样的hash将plaintext 映射到 G1，而是直接从G1中随机产生一个元素作为 message。

下面介绍如何自己生成一些参数:

在manual中，有：

void pairing_init_pbc_param(struct pairing_s *pairing, pbc_param_t p)

又在Param generation中有以下的一些函数：

void pbc_param_init_a_gen(pbc_param_t par, int rbits, int qbits)

Generate type A pairing parameters and store them in p, where the group order r is rbits long, and the order of the base field q is qbits long. Elements take qbits to represent.

To be secure, generic discrete log algorithms must be infeasible in groups of order r, and finite field discrete log algorithms must be infeasible in finite fields of order q^2, e.g. rbits = 160, qbits = 512.

The file param/a.param contains parameters for a type A pairing suitable for cryptographic use.

void pbc_param_init_a1_gen(pbc_param_t param, mpz_t n)

Generate type A1 pairing parameters and store them in p. The group order will be n. The order of the base field is a few bits longer. To be secure, generic discrete log algorithms must be infeasible in groups of order n, and finite field discrete log algorithms must be infeasible in finite fields of order roughly n². Additionally, n should be hard to factorize.

For example: n a product of two primes, each at least 512 bits.

The file param/a1.param contains sample parameters for a type A1 pairing, but it is only for benchmarking: it is useless without the factorization of n, the order of the group.

Initialize a pairing with pairing parameters p.

在

在源码pbc_pairing.h中有以下定义： 

typedef struct pairing_s pairing_t[1];
 typedef struct pairing_s *pairing_ptr;

所以我们可以直接这样加以初始化：

 pbc_param_t param;
     pbc_param_init_a1_gen(param, NN);
     pbc_param_out_str(stdout, param);
     
     pairing_t pairing;
     pairing_init_pbc_param(pairing, param);

使用前首先要选择已经初始化pairing_t，其将初始化内部诸如椭圆曲线的设置，各种内在数学群结构的设置等等。