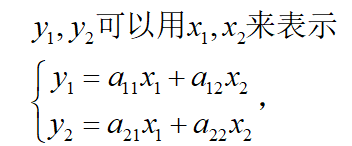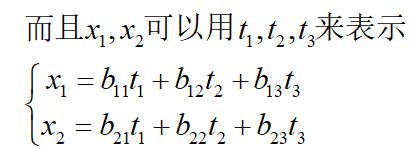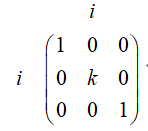最近在学习线性代数的课,复习相关知识,加深理解,争取做到在碰到矩阵问题时能立马联系到书本中的相关知识点。
1.线性方程组
清华大学出版社出版、王萼芳编著的《线性代数》不同于一般线性代数教材的一点是,它在行列式的概念之前提出了矩阵的概念,而矩阵的运算、分块、求逆被放在行列式之后讲解。这样布置的好处是,可以先学习线性方程组的求解,搞清楚线性代数学习的第一个目标就是解决线性方程组的解的存在与否的判别和求解(如果存在),这样的学习从传统的线性方程组的求解方法:消元法开始,与中学阶段知识保持连续性。当然也有缺点,为了解决非齐次线性方程组的求解问题,该书在第二章就开始讲解n维向量空间、向量组的线性相关性、向量组的秩,这里的学习难度曲线就有些陡峭了。
1.1消元法的3种基本变换:
1)用一个非零的数乘一个方程;k*Ri,
2)用一个数乘一个方程后加到另一个方程上;Rj+k*Ri,
3)互换两个方程的位置;Rij,
以上3种变换称为线性方程组的初等变换。
1.2线性方程组的矩阵
消元法的目的是得到阶梯形方程组。
线性方程组可以用增广矩阵A(hat)来表示。
对应于消元法的3种变换,矩阵初等行变换是指下列3种变换:
1)用一个非零的数乘矩阵的一行;k*Ri,
2)把矩阵的某一行乘k后加到另一行上;Rj+k*Ri,
3)互换矩阵中两行的位置;Rij,
定义:矩阵A经过初等行变换化为阶梯形矩阵后,阶梯形矩阵中非零行的个数称为矩阵A的秩,记作r(A) 。
定理:线性方程组有解的充分必要条件是它的系数矩阵A与增广矩阵A(hat)的有相同的秩。
定理:线性方程组有解时,如果它的系数矩阵的秩r等于未知量个数n,则方程组有唯一解;如果r 2. n维向量空间 n维向量定义:数域P中n个数组成的有序数据(a1,a2,...,an)称为数域P上的一个n维向量。两个n维向量的对应分量都相等,则这两个向量相等。 n维向量的运算,包括加法、减法、数乘,统称为向量的线性运算。向量的线性运算有8条基本法则。 n维向量空间的定义:数域P上的n维向量的全体,同时考虑到定义在它们上面的线性运算,称为数域P上的n维向量空间,记做Pn。 向量之间的关系:两个向量之间,最简单的关系是成比例,所谓向量α与β成比例,就是说有一个数k,使得α=k·β。在多个向量之间,成比例的关系表现为线性组合。 线性表出:若存在数域P中的数k1,k2,...,ks,使得数域P上的n维向量空间中的一些向量之间满足下列关系:α=k1·β1+k2·β2+...+ks·βs,就说α是β1,β2,...,βs的一个线性组合。也可以说α可以由β1,β2,...,βs线性表出。如果两个向量组可以互相线性表出(一组内每个成员向量都可以用另一向量组线性表出),就称它们是等价的。 线性相关:对于数域P上向量组 由n维基本向量 向量组的线性相关性与以该向量组作为系数矩阵的齐次线性方程组有无非零解是有紧密联系的,也与向量组内向量之间能否线性表出是有关系的,存在一系列定理。 极大线性无关组定义:向量组的一个部分组称为它的一个极大线性无关组,如果这个部分组本身是线性无关的,但是再从原向量组的其余向量(如果还有的话)中任取一个添加进去以后,所得到的部分组都线性相关。定理:向量组的任意一个极大线性无关组都与向量组本身等价。向量组的极大线性无关组所含向量的个数称为这个向量组的秩。等价的向量组必有相同的秩。 重要定理:矩阵A的秩等于它的行向量组的秩,也等于它的列向量组的秩。即:行(列)向量组极大无关组所含向量的个数=矩阵的秩。 证明: 该定理的作用:给出了一种求向量组秩的方法,就是应用矩阵的初等行变换,求矩阵的秩即可。 截至目前,我们对于n阶可逆矩阵A,可以有推论如下: 2.4线性方程组解的结构 方程组只有唯一解的情形,直接把这个解求出来即可。在方程组有无穷多个解的情况下,所谓解的结构问题,就是解与解之间的关系问题。用消元法解线性方程组的时候,给出了一般解(给出了每个解的一般表达式),而这里则是应用向量的概念来证明,全部的解(无穷多个解的情形下)都可以用有限多个解表示出来。 首先考察: 所以有: 如果齐次线性方程组AmxnX=0的r(A) 怎么找?过程就是将系数矩阵A进行行初等变换,化为约化阶梯形,得到r(A)=r,并取n-r个自由变量,得到方程组的通解,再将通解改写为向量的形式: 由极大线性无关组的性质可以推出: 非齐次线性方程组解的结构定理: 证明略。 值得注意的是,导出组的解空间是有基础解系(基)的,而AX=b的解空间中是不存在基础解系的,只能写出其极大线性无关组,如下: 证明: 3.行列式 引进行列式的目的是,为了直接用线性方程组的系数及常数项来判断方程组是否有解、将解表示出来,也就是所谓的克莱默法则。 为了理解行列式的概念,我们就要进行行列式的计算。通过观察,发现行列式可以通过按行展开来计算,也有如范德蒙德行列式等特殊的行列式直接可用公式计算出来。在以前的学习中,第一章就是讲行列式,一上来就是让你算各种行列式的值,在考试中往往计算行列式变成一个非常大的分数点,但其实行列式的计算并没有那么重要,这一章里最重要的还是克莱默法则。 附上克莱默法则的百度百科:https://baike.baidu.com/item/克莱姆法则/7211518?fr=aladdin 在老师上课过程中,基本上只会讲一下克莱默法则是什么内容,然后会结合例子的讲解来展示克莱默法则基本的运算过程,但是基本法则不会去证明,有兴趣的需要自己课后去学习,这也说明大学的课程,还是注重自己预习复习、自学自练的。 4.矩阵的运算、逆 本章讲的矩阵,是从一般意义上来研究矩阵的,而不再默认把矩阵应用于求解线性方程组。矩阵的本质就是矩形数表。 将矩阵的秩与行列式结合起来,可以这样定义:矩阵的最高阶非零子式的阶,就是矩阵的秩。但是按照这种定义,去找矩阵的秩并不太好找,因为涉及到从n阶、n-1阶、n-2阶等顺序计算的许多余子式的计算。一般还是采取将矩阵化简为阶梯形,数非零行数来求秩。 4.1矩阵的运算 矩阵运算有加法、数乘,以及乘法,转置。其中加法和数乘也满足8条运算法则,和n维向量空间中的8条运算法则一致。一般书本中,先讲的矩阵,再讲的线性空间,所以讲解矩阵时的8条运算法则,是为后续讲线性空间埋下伏笔。线性空间的概念,是n维向量空间的抽象化。 PS:虽然n维向量空间已经是几何空间的推广了,但是在一些数学问题和实际问题中,还会遇到许多其它对象(不仅是有序数组),我们也可对其进行线性运算,为了对它们统一地加以研究,有必要使向量的概念更为一般化,推广向量的涵义,将n维向量空间抽象化,就得到线性空间的概念。 矩阵的乘法的来源 矩阵的乘法:1.一般不交换,即一般AB≠BA;2.一般不消去,即:若AB=AC,未必B=C。若AB=0,未必A=0或B=0;3.满足结合律;4.满足分配律。 矩阵多项式:由矩阵A和系数组成的形如 为何要对矩阵多项式感兴趣呢?老师说这是因为矩阵多项式满足交换律,比如:A2-2A-3E=(A-3E)(A+E)=(A+E)(A-3E) 4.2矩阵的逆 “矩阵的逆”的目的 矩阵的运算有加减乘,但是没有除法。引进逆矩阵,是一种实现矩阵除法的手段。 当然书本里,并没有这么说。跟老师交流,他认为逆矩阵是为了有助于矩阵多项式的计算。 “矩阵的逆”的求解方法 第一种,当然是通过矩阵的逆的定义来求解,通过伴随矩阵A*与行列式|A|相除得到; 第二种,通过矩阵的初等行变换来求解,将(A|E)施行初等行变换,将A变为E,同时能够实现E变为A,即(E|A)。 这里涉及到几个知识点,满秩(可逆)矩阵A总是能够通过一系列初等行变换化为单位矩阵E。 4.3矩阵的分块 矩阵的分块看似挺简单,但是深入进去理解应该挺难的,老师说分块的功底、秩的功底决定了线性代数的功底。 4.5初等变换和初等矩阵 学习初等变换和初等矩阵的目的:(1)把矩阵的初等变换中的箭头"→"改为"=";(2)给出求逆矩阵A-1的第二种方法(前面已经讲过)。 初等变换共有三大类6小类: (1).互换;(2).倍乘;(3).倍加。 初等变换是保秩的。 为了实现上述2个目的,先介绍另一个概念,初等矩阵。定义:把单位矩阵E经过一次初等行、列变换所得的矩阵,称为初等矩阵。同样初等矩阵也有三大类六小类。 重要结论:对矩阵A进行初等行变换,就用同样的初等矩阵左乘它;对矩阵A进行初等列变换,就用同样的初等矩阵右乘它。 四个推论: 1)m*n阶矩阵A,若rank(A)=r,由于它经过6种初等变换一定可以化为 2)m*n阶矩阵A,若rank(A)=r,由于它经过6种初等变换一定可以化为 3)方阵A可逆的充分必要条件是A可以写成初等矩阵的乘积。 4)若方阵A可逆,则rank(AC)=rank(C)=rank(CA). 矩阵等价的定义:如果矩阵B可以从矩阵A经过一系列的初等变换而得到,则称矩阵A与B是等价的。 因此可以这么理解,等价是矩阵之间的关系,这种关系可以由一系列小关系(多次初等变换)组成。 5.矩阵的对角化问题 矩阵相似的定义:对于阶数相同的方阵A和B, 若存在可逆方阵P, 使得P-1AP=B. 则称矩阵A与B相似, 记为A˜B, 而对A进行的运算P-1AP称为对A进行的相似变换, 可逆方阵P称为把A变为B的相似变换矩阵。 因此,相似也是矩阵之间的一种关系,这种关系比矩阵等价要强。![]() ,如果有数域P中不全为零的数k1,k2,...,ks,使得如下等式成立:
,如果有数域P中不全为零的数k1,k2,...,ks,使得如下等式成立:![]() ,则称向量组
,则称向量组![]() 线性相关。
线性相关。![]() 组成的向量组是线性无关的。
组成的向量组是线性无关的。 。还得证明3点:
。还得证明3点: ,第3点比较困难,可以改证W的维数是n-r维的(dimW=n-r)。
,第3点比较困难,可以改证W的维数是n-r维的(dimW=n-r)。![]() 的式子,叫做矩阵多项式。
的式子,叫做矩阵多项式。 的形式,因此一定存在m阶初等矩阵P1,P2,...,Ps,n阶初等矩阵Q1,Q2,...,Qt,使得
的形式,因此一定存在m阶初等矩阵P1,P2,...,Ps,n阶初等矩阵Q1,Q2,...,Qt,使得 的形式,因此一定存在m阶可逆矩阵P和n阶可逆矩阵Q,使得
的形式,因此一定存在m阶可逆矩阵P和n阶可逆矩阵Q,使得 。
。