卡尔曼滤波，互补滤波，“Tsinghua”滤波

昨天，有同学在公众号提出一个问题。从问题来看，他应该是在准备今年的节能平衡自行车组别的智能车竞赛。

卓大大，请问您可以针对卡尔曼滤波、互补滤波、清华滤波的原理与异同做一个推送吗？最近在查阅相关的资料学习滤波算法，感觉好难理解呀/::<

^{▲ 平衡双轮自行车}

由于近期相关四旋翼飞机、平衡车、活动机器人等领域都需要对控制对象的姿态进行感知，因此 卡尔曼(Kalman)滤波器 、 互补滤波器 的基本原理，以及它们之间的 实验比较 等相关的资料在网路上早已广泛存在了。下面的内容希望能够帮助最初接触这块内容的同学掌握理解这方面的内容。

同学们之所以提到对这三种算法进行比较，是因为对智能车竞赛中平衡车模控制算法中对于车模姿态（实际上只有车模前倾角以及角速度）进行测量中，需要融合惯性测量传感器（陀螺仪和加速度计）的输出数据，在以往比赛中很多同学使用了这三种算法，它们之间有着很深的联系 。

谈到滤波器，它的一个作用就是将信号中的噪声去除。线性滤波器是一种广泛使用的方法，前面提到的三种方法都是属于线性滤波器，这样就可以通过它们的 传递函数 、频率特性等多方面进行对比。

为了分析这三种算法在控制平衡车模中的联系，就需要先从车模姿态传感器存在的问题分析出发，讨论解决的方案，逐步扩展到三种滤波算法。

 

01问题来源

---

用于测量平衡车模姿的惯性传感器主要包括两种：陀螺仪和加速度计。

1.陀螺仪的特性

陀螺仪输出的信号$V_G\left(t\right)$反映角速度$\dot{\theta }\left(t\right)$。通过对角速度的积分，便可以得到相应的角度。通常，在平衡车模直立控制中，需要角度、角速度两个量，通过一定的加权系数作为反馈量来控制电机输出力矩，从而维持车模的基本平衡。

下图给出了一个模拟陀螺仪输出的电压信号与转动之间的关系。

^{▲ 陀螺仪输出信号}

在陀螺仪静止的时候，输出一个电压常量$V_{G0}$，随着它的转动输出电压便上下浮动。

将陀螺仪输出的电压$V_G\left(t\right)$，减去静态$V_{G0}$，然后进行积分，便可以得到一个与角度成正比的量：$$K\cdot \theta \left(t\right)={\int }_{-\infty }^t{V}_G\left(\tau \right)-V_{G0}d\tau$$

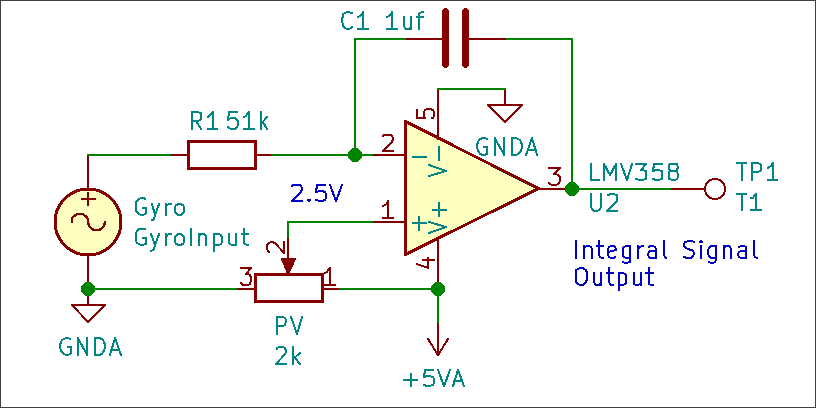
下图给出单电源运放组成的积分电路。调整电位器PV，使得它的电压等于陀螺仪静止时的常量$V_{G0}$，这样输出电压便与传感器倾角成正比。

^{▲ 对陀螺仪信号进行积分}

下图反映了该信号经过积分之后的信号。随着传感器在不同的角度，输出电压在处在不同的电压范围之内。

^{▲ 陀螺仪的积分信号反映了角度}

作为积分电路，本身它是一个不稳定系统。由于这种原因（陀螺仪静态电压漂移、运放偏置电压的漂移等）会使的积分输出电压会随着时间发生积分偏移。不仅使得输出角度出现误差，而且也会使得运发进入饱和而失去作用。

下图显示了陀螺仪在静止状态下，上面的积分电路输出逐步发生积分偏移，最终达到饱和的过程。

^{▲ 陀螺仪积分信号不稳定性}

因此，只使用陀螺仪则无法获得稳定准确传感器的姿态角度。

为了消除信号中的直流偏移，可以通过隔直电容来完成。下图显示了RC电路完成信号的直流隔离。为了保护运放不受直流偏移量的影响，将RC隔直电路移到积分电路的输入端。

^{▲ 在陀螺仪积分电路上增加RC高通滤波}

在下图中显示了增加隔直电容后的积分电路。其中R3并联在原来的积分电容C1两端，是为了抑制运放偏置电压的漂移对输出的影响。$R_3,C_1$组成的时间常数大约是10秒钟。

C3是对输出电压中点参考电压进行滤波。

^{▲ 带有RC隔直陀螺仪积分电路}

在积分电路的输入端增加了隔直电容C2，又在积分电容C1上并联了R3，这就抑制了积分电路的积分漂移。

下图显示了积分电路输出电压将会稳定在一个固定电压的过程。

^{▲ 增加隔直后电容消除零点漂移}

上述电路虽然抑制了角度速度积分的漂移。但对于角度信号中的低频分量也有很大的抑制。

将模块固定在一个确定的倾角，输出电压开始变化到相应的输出电压滞后，便逐渐向静态工作点进行衰减。

^{▲ 对姿态低频信息的丢失}

测图测量了陀螺仪经过积分后的输出信号。可以看到积分信号能够快速跟踪角度的变化。但是当陀螺仪一旦静止，输出电压值便向输出稳定值衰减。

^{▲ 陀螺仪输出及其隔直积分输出}

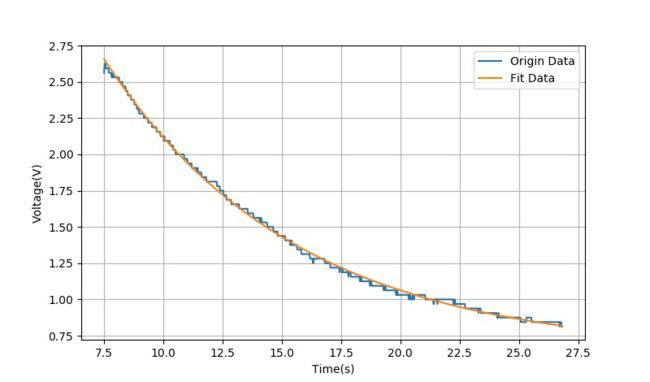
通过截取角度衰减曲线中7.5秒之后的数据，可以测量衰减的时间常数。对上面数据中陀螺仪输出信号的衰减曲线数据进行指数建模，可以得到拟合公式为：

$$y\left(t\right)=5.14\cdot e^{-\frac{t}{8.04}}+0.6347$$

时间常数为8秒钟。反映了陀螺仪积分输出的稳态值，每经过8秒钟，输出值便衰减到原来的$1/e=0.367$。

^{▲ 输出曲线的7.5秒~27.5秒的电压曲线以及指数拟合曲线}

$$y\left(t\right)=5.14\cdot e^{-\frac{t}{8.04}}+0.6347$$

2. 加速度计特性

加速度计可以输出一个与传感器加速度成正比的电压量。由于加速度是一个矢量，输出的电压量与加速度绝对值$A$以及加速度与传感器敏感方向之间的夹角$\varphi$都有关系。具体关系如下：$$V_A=k\cdot A\cdot \cos \left(\varphi \right)$$

使用加速度来测量倾角主要是利用地球重力场加速度矢量$\bar{g}$，近似一个恒定加速度。此时将加速度的敏感方向与$\bar{g}$保持垂直。此时传感器的倾角$\theta \left(t\right)$与传感器输出电压$V_A\left(t\right)$之间就是正弦关系：$$V_A\left(t\right)=k\cdot A\cdot \sin \left[\theta \left(t\right)\right]$$

当角度$\theta \left(t\right)$小的时候，它就可以近似与加速度传感器输出成正比：$V_A\left(t\right)=K_a\cdot \theta \left(t\right)$。

下图显示了加速度传感器输出与传感器在不同位置之间的关系。

^{▲ 加速度计输出特性}

由于传感器随着车模运动会产生额外的加速度$a\left(t\right)$，它也会在加速度传感器上产生相应的电压波动。这就干扰了作为姿态倾角信号的输出。

下图显示了手拿着姿态传感器水平晃动，保持传感器倾角不变，加速度传感器输出电压的波动情况。

^{▲ 加速度计输出受到运动加速度的干扰}

为了减少运动所引起加速度输出信号的波动，可以通过低通滤波器对它进行平滑。

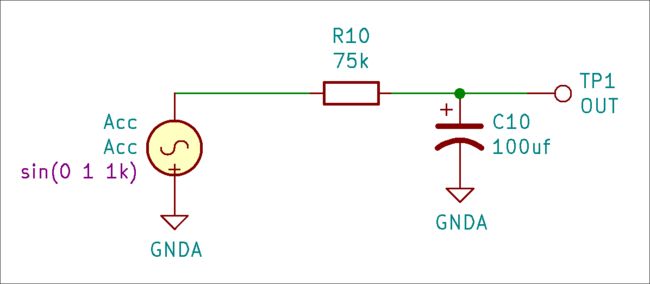
下图是一个RC一阶低通滤波器，可以对信号的波动进行平滑。根据图中$R_{10},C_{10}$的参数，滤波器的时间常数大约是$\tau =R_{10}\cdot C_{10}=7.5s$。

^{▲ 使用RC低通滤波器平滑加速度传感器输出信号}

下图给出了加速度信号（青色）经过上面低通滤波器之后的输出信号（黄色），前面由于晃动引起的输出信号波动，经过滤波之后基本上都消失了。

但是，这种滤波也带来了另外一个问题，就是输出信号不能够及时反映角度的变化了。

^{▲ 加速度计经过RC滤波后的波形}

通过对测量数据中角度变化曲线（黄色曲线）进行建模分析，可以得到实际信号延迟时间常数。

对黄色曲线进行指数拟合，可以得到以下表达式：
$$y\left(t\right)=-1.263\cdot e^{-\frac{t}{9.008}}+2.354$$

对应的时间常数$${\tau }_{RC}=9.008s$$
比RC低通滤波器的时间常数（7.5秒）大了近1.5秒。这说明加速度传感器输出内阻大约为15kΩ左右。

^{▲ 对滤波后的信号进行拟合结果}

 

02初步解决方案

---

^{▲ 陀螺仪（黄色）加速度计（青色）滤波后的输出波形}

^{▲ 陀螺仪和加速度输出信号融合
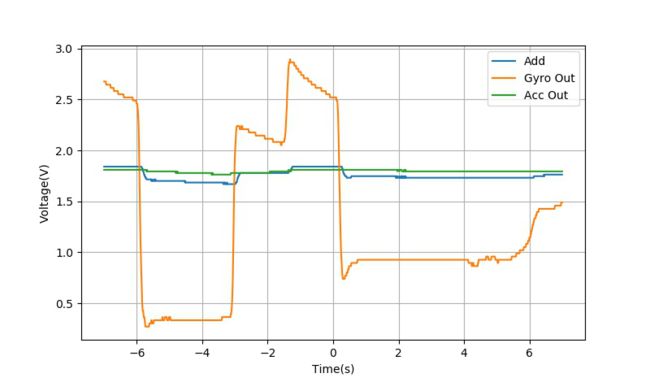
▲ Gyro比例过大的情况}

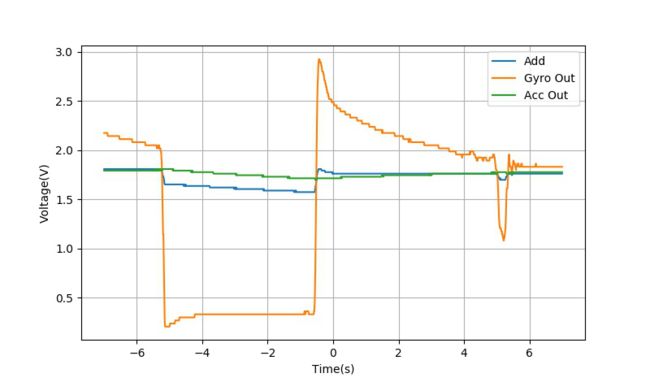
^{▲ Gyro比例过小}

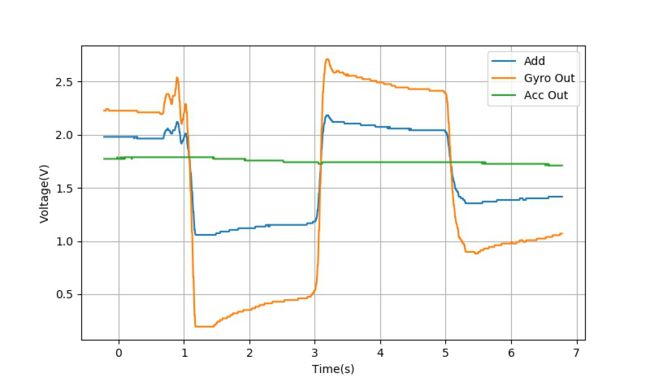
^{▲ Gyro比例基本合适}

^{▲ 互补滤波后的结果}