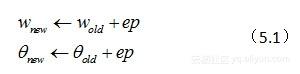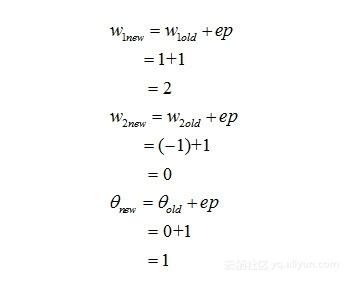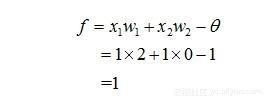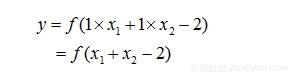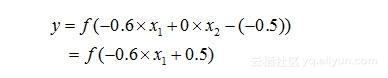Hello World感知机,懂你我心才安息 (深度学习入门系列之五)
原文再续,书接上回。
5.1 网之初,感知机
我们知道,《三字经》里开篇第一句就是:“人之初,性本善”。那么对于神经网络来说,这句话就要改为:“网之初,感知机”。感知机( Perceptrons ),基本上来说,是一切神经网络学习的起点。
很多有关神经网络学习(包括深度学习)的教程,在提及感知机时,都知道绕不过,但也仅仅一带而过。学过编程的同学都知道,不论是哪门什么语言,那个神一般存在的第一个程序——“Hello World”,对初学者有多么重要,可以说,它就是很多人“光荣与梦想”开始的地方。
而感知机学习,就是神经网络学习的“Hello World”,所以对于初学者来说,也值得我们细细玩味。因此,下面我们就给予详细讲解。
5.2 感性认识“感知机”
在第3小节中,我们已经提到,所谓的感知机,其实就是一个由两层神经元构成的网络结构,它在输入层接收外界的输入,通过激活函数(含阈值)的变换,把信号传送至输出层,因此它也称之为“阈值逻辑单元(threshold logic unit)”。
麻雀虽小,五脏俱全。感知机虽然简单,但已初具神经网络的必备要素。在前面我们也提到,所有“有监督”的学习,在某种程度上,都是分类(classification)学习算法。而感知机就是有监督的学习,所以,它也是一种分类算法。下面我们就列举一个区分“西瓜和香蕉”的经典案例,来看看感知机是如何工作的[1]。
为了简单起见,我们就假设西瓜和香蕉都仅有两个特征(feature):形状和颜色,其它特征暂不考虑。这两个特征都是基于视觉刺激而得到的。
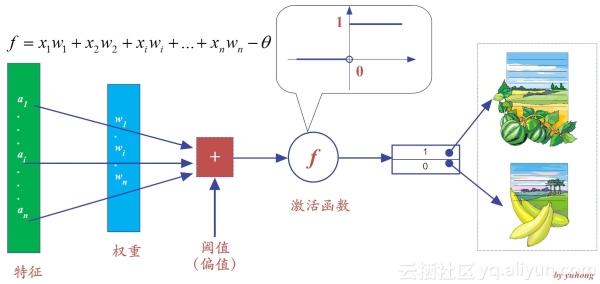
图5-1 感知机学习算法
假设特征x1代表输入颜色,特征x2代表形状,权重w1和w2默认值都为1,为了进一步简化,我们把阈值θ(亦有教程称之为偏值——bias)设置为0。为了标识方便,我们将感知器输出为“1”,代表判定为“西瓜”,而输出为“0”,代表判定为“香蕉”。当然了,如果有更多类别的物品,我们就用更多的数字来标记即可。
为了方便机器计算,我们对颜色和形状这两个特征,给予不同的值,以示区别。比如,颜色这个特征为绿色时,x1取值为1,而当颜色为黄色时,x1取值为-1;类似地,如果形状这个特征为圆形,x2取值为1,反之,形状为弯曲状时,x2取值为-1,如表5-1所示。
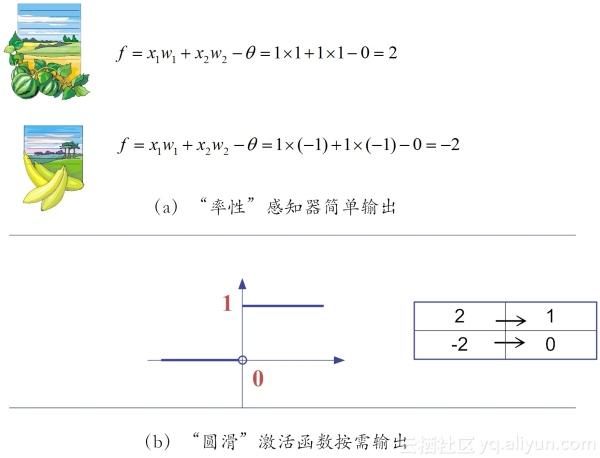
这样一来,可以很容易依据图5-1所示的公式,对于西瓜、香蕉做鉴定(即输出函数f的值),其结果分别如图5-2(a)所示:
图5-2 感知器的输出
从图5-2(a)所示的输出可以看到,对西瓜的判定输出结果是2,而香蕉的为-2。而我们先前预定的规则是:函数输出为1,则判定为西瓜,输出为0,则判定为香蕉,那么如何将2或-2这样的分类结果,变换成预期的分类表达呢,这个时候,就需要激活函数上场了!
这里,我们使用了最为简单的阶跃函数(step function)。在阶跃函数中,输出规则非常简单:当x>0时,f(x)输出为1,否则输出0。通过激活函数的“润滑”之后,结果就变成我们想要的样子(如图5-2-b所示)。就这样,我们就搞定了西瓜和香蕉的判定。
这里需要说明的是,对象的不同特征(比如水果的颜色或形状等),只要用不同数值区分表示开来即可,具体用什么样的值,其实并无大碍。
但你或许会疑惑,这里的阈值(threshold)θ和两个连接权值w1和w2,为啥就这么巧分别就是0、1、1呢?如果取其它数值,会有不同的判定结果吗?
这是个好问题。事实上,我们并不能一开始就知道这几个参数的取值,而是一点点地非常苦逼地“折腾试错”(Try-Error)出来的,而这里的“折腾试错”其实就是感知机的学习过程!
下面,我们就聊聊最简单的神经网络——感知机它是如何学习的?
5.3 感知机是如何学习的?
中国有句古话:“知错能改,善莫大焉。”说得就是“犯了错误而能改正,没有比这更好的事了”。
放到机器学习领域,这句话显然属于“监督学习”的范畴。因为“知错”,就表明它事先已有了事物的评判标准,如果你的行为不符合(或说偏离)这些标准,那么就要根据“偏离的程度”,来“改善”自己的行为。
下面,我们就根据这个思想,来制定感知机的学习规则。从前面讨论中我们已经知道,感知机学习属于“有监督学习”(即分类算法)。感知机是有明确的目的导向的,这有点类似于“不管白猫黑猫,抓住老鼠就是好猫”,不管是什么样的学习规则,能达到良好的分类目的,就是好学习规则。
我们知道,对象本身的特征值,一旦确定下来就不会变化。因此,所谓神经网络的学习规则,就是调整权值和阈值的规则(这个结论对于深度学习而言,依然是适用的)。
假设我们的规则是这样的:
其中ep = y-y’,y为期望输出,y’是实际输出,所以,具体说来,ep是二者的差值。在后面,读者朋友可以看到,这个“落差”就是整个网络中权值和阈值的调整动力。因为,很显然,如果ep为0,那么新、旧权值和阈值都是一样的,网络就稳定可用了!
下面,我们就用上面的学习规则来模拟感知机的学习过程。假设w1和w2初始值分别为1和-1(注意:已经不再是1和1了!),阈值θ依然为0(事实上为其它初值,也是可行的),那么我们遵循如下步骤,即可完成判定西瓜的学习:
(1)计算判定西瓜的输出值f:
将这个输出值带入如图5-2-b所示的阶跃函数中,可得y=0。
(2)显然,针对西瓜,我们期望输出的正确判定是:y=1,而现在实际输出的值y’=0,也就是说,实际输出有误。这个时候,就需要纠偏。而纠偏,就需要利用公式(5.1)所示的学习规则。于是,我们需要计算出来误差ep来。
(3)计算误差ep:
现在,我们把ep的值带入公式(5.1)所示的规则中,更新网络的权值和阈值,即:
(3)那么,在新一轮的网络参数(即权值、阈值)重新学习获得后,我们再次输入西瓜的属性值,来测试一下,看看它能否正确判定:
再经过激活函数(阶跃函数)处理后,输出结果y=1,很高兴,判定正确!
(4)我们知道,一个对象的类别判定正确,不算好,“大家好,才算真的好!”于是,在判定西瓜正确后,我们还要尝试在这样的网络参数下,看看香蕉的判定是否也是正确的:
类似地,经过激活函数(阶跃函数)处理后,输出结果y=0,判定也正确的!BINGO!误差ep为0,打完收工,学习结束!
在这个案例里,仅仅经过一轮的“试错法(trial-by-error)”,我们就搞定了参数的训练,但你可别高兴太早,谁叫这是一个“Hello World”版本的神经网络呢!事实上,在有监督的学习规则中,我们需要根据输出与期望值的“落差”,经过多轮重试,反复调整神经网络的权值,直至这个“落差”收敛到能够忍受的范围之内,训练才告结束。
在上面,我们仅仅给出了感知机学习的一个感性例子,下面我们要给出感知机学习的形式化的描述。
5.4 感知机的训练法则
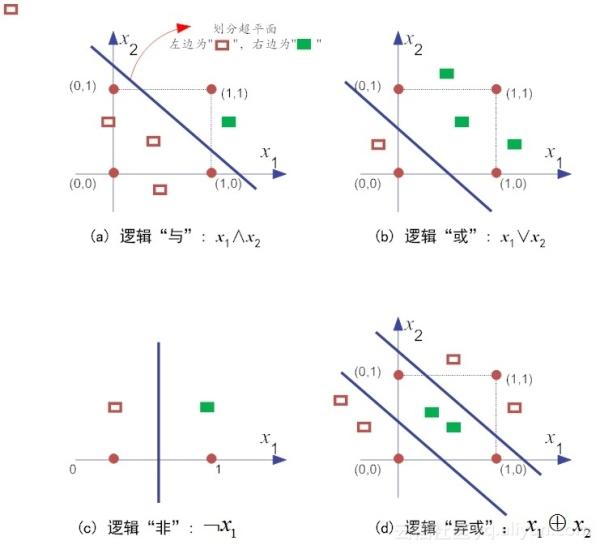
通过前面的分析,我们可以看到,感知机是很容易实现逻辑上的“与(AND)”、“或(OR)”、“非(NOT)”等原子布尔函数(Primitive Boolean function),如图5-3所示(睿智如你,你肯定发现了,这里的确没有“异或”,这个坑回头我们在后面再填上)[2]。
图5-3 感知机实现逻辑运算
下面举例说明。首先,我们注意到,假设f是如图5-3所示的阶跃函数,通过合适的权值和阈值,即可完成常见的逻辑运算(既然是逻辑运算,x1和x2都只能取值为0或1),例如:
(1)“与(x1∧x2)”:当权值w1=w2=1,阈值θ=2时,有:
此时,仅当x1=x2=1时,y=1,而在其它情况下(如x1和x2无论哪一个取0),y=0。这样,我们在感知机中,就完成了逻辑“与”的运算。
(2)类似地,“或(x1∨x2)”:当w1=w2=1,阈值θ=0.5时,有:
此时,当x1或x2中有一个为“1”时,那么y=1,而在其它情况下(即x1和x2均都取“0”),y=0。这样,我们就完成了逻辑“或”的运算。
(3)在类似地,“非(┐x1)”:当w1=0.6,w2=,0,阈值θ=0.5时,有:
此时,当x1为“1”时,y=0,当x1为“0”时,y=1。这样,就完成了逻辑“非”的运算(当然,如果以x2做“非”运算,也是类似操作,这里不再赘述)。
更一般地,当我们给定训练数据,神经网络中的参数(权值wi和阈值θ)都可以通过不断地“纠偏”学习得到。为了方便起见,我们把阈值θ视为w0,而其权值设为固定值“-1”,那么阈值θ就可视为一个“哑节点(dummy node)”。这样一来,权重和阈值的学习可以“一统天下”称为“权重”的学习。
如此一来,感知机的学习规则就可以更加简单明了,对于训练样例(x,y)(需要注意的是,这里粗体字x表示训练集合),若当前感知机的实际输出y’,假设它不符合预期,存在“落差”,那么感知机的权值依据如公式(5.2)规则调整:
其中,η∈(0,1)称为学习率(learning rate),公式(5.2)其实是公式(5.1)的一般化描述。由公式(5.2)可知,如果(x,y)预测正确,那么可知y=y’,感知机的权值就不会发生任何变化,否则就会根据“落差”的程度做对应调整。
这里需要注意的是,学习率η的作用是“缓和”每一步权值调整强度的。它本身的大小,也是比较难以确定的。如果η太小,网络调参的次数就太多,从而收敛很慢。如果η太大,“步子大了,容易扯着蛋”,从而错过了网络的参数的最优解。因此,合适的η大小,在某种程度上,还依赖于人工经验(如图5-4所示)。
图5-4 学习率:“步子大了,容易扯着蛋”
5.5 感知机的表征能力
如果识别对象x有n个特征,那么感知机可以看做,在n维实例空间(即点空间)中的超平面决策面,以向量的模式写出来就是如图5-5所示。
图5-5 感知机的超平面
这样一来的话,对于超平面一侧的实例,感知机输出为1(或称判定为某一类),而对于超平面的另外一侧实例,感知机输出为0(判定为另外一类)。
由于感知机只有输出层神经元可以进行激活函数的处理,也就是说它只拥有单层的功能元神经元(functional neuron),因此它的学习能力是相对有限的。比如说在5.4小节中,原子布尔函数中的“与、或、非”等问题都是线性可分的(linearly separable)的问题。
前面的章节中,我们提到的那位人工智能泰斗明斯基(Minsky)已经证明,若两类模式是线性可分的,那么一定存在一个线性超平面可以将它们区分开来,如图5-6(a)-(c)所示。也就是说,这样的感知机,其学习过程一定会稳定(即收敛)下来,神经网络的权值可以学习得到。
但是对于线性不可分原子布尔函数(如“异或”操作),就不存在简单地线性超平面将其区分开来(如图5-6-(d))。在这种情况下,感知机的学习过程就会发生“震荡(fluctuation)”,权值向量就难以求得合适解。这里稍微为非专业读者解释一下什么异或?所谓异或(XOR),就是当且仅当输入值x1和x2不相等,则输出为1。反之,输出为0。你可以监督粗暴地把“异或”理解为:男欢女爱输出为1,搞基都是没有结果的(输出为0)!
图5-6 线性可分的“与、或、非”和线性不可分的“异或”
一个寄以厚望的感知机,居然连简单的“异或”功能都实现不了,这点让明斯基颇为失望。于是,在1969年,他和同事Papert合作写下《感知机》一书[3],直接把“感知机”判了个n年有期徒刑(n在当时为不可知变量)。
这么一说,好像明斯基是一位法官一样。但其实呢,他更像《白雪公主》里的那位继母王后。这是因为就是他,给那个叫“人工智能”的“白雪公主”喂了一颗“毒苹果”(《感知机》一书),让这位“白雪公主”一睡就是20年(n=20)。
我们知道,绝大多数童话都有个“happy ending(完美结局)”,《白雪公主》也不例外。现在我们好奇的是,在人工智能领域,谁又是那位“吻醒”白雪公主的“王子”呢?
欲知后事如何,且听我们下回分解。
5.6小结
在本小节,我们首先用西瓜和香蕉的判定案例,感性地谈了谈感知机的工作流程。然后,我们又给出了感知机的形式化学习规则以及感知机的表征能力。容易发现,感知机连常见的逻辑操作“异或”都难以实现,这一功能缺陷,直接让人工智能领域大神明斯基抓住了“小辫子”,然后就把“人工智能”送进了长达二十年的“冬天”。
但英国浪漫主义诗人雪莱说了:“冬天来了,春天还会远吗?”
5.7 请你思考
学习完本小节,请你思考如下问题:
(1)你能参照感知机判定“西瓜”和“香蕉”的案例,训练感知机完整布尔函数“与、或、非”等权值的学习吗?请用编程语言实现。(提示:它山之石,可以攻玉。可以借助开源的神经网络框架实现,如由Java语言编写的Neuroph,下载链接:Java Neural Network Framework Neuroph)
(2)你知道最终感知机是如何解决“异或”问题的吗?(提前剧透:增加神经网络的层数,提升网络数据特征的表达能力,网络层次多了,这就是深度神经网络啊!)
写下你的感悟,祝你每天都有收获!
【参考文献】
[1] 吴岸城. 神经网络与深度学习.电子工业出版社.2016.6
[2] 周志华.机器学习.清华大学出版社.2016.2
[3] Minsky M, Papert S. Perceptrons[J]. 1969.