开学第十二周.two(Disjoint Set)
建议看新版:并查集总结(不看后悔系列)
果然成功是留给有准备的人的。今天的测试赛只A了两道,看着其他人A四五道题,我不由的说出一开始的这句话,通过这次测试我也找到自己一个很大的毛病——不主动学习新知识,一味寻求被动接受,还有时间花的不合理,使用的效率不高。这样下去我感觉自己很危险啊,不行!必须要改!总的来说付出的还不够多。
今天测试赛C题是一道并查集的模板题,以前也多次看到过这个名字,听起来就很难的样子,学会知难而上,今天就学习一下吧。
英文:Disjoint Set(Union-Find-Set),即“不相交集合”
将编号分别为1…N的N个对象划分为不相交集合,
在每个集合中,选择其中某个元素代表所在集合。
常见两种操作:
> 合并两个集合
> 查找某元素属于哪个集合
所以,也称为“并查集”.
合并操作:
void join(int x,int y)
{
int p,q;
p=Find(x);
q=Find(y);
if(p!=q) {
pre[p]=q;
}
}
//or
void join(int x,int y)
{
pre[Find(x)] = Find(y);
}
查找操作(同时压缩路径):
为了防止变为链状,一般有两种优化,路径压缩和按秩合并。一般路径压缩就够了,按秩合并的话是在合并是让深度低的树并到深度高的树上,最小可能的减少树的规模。(下边的检查环就是按秩合并优化)
//递归形式,但当数据量大时容易爆栈
int Find(int x)
{
if(pre[x]!=x) pre[x]=Find(pre[x]);
return pre[x];
}
//or
int Find(int x)
{
return x == pre[x]?x:pre[x] = Find(pre[x]);
}
//循环,以防大量数据导致爆栈
int Find(int x)
{
int p,temp;
p=x;
while(x!=pre[x])
x = pre[x];
while(p!=x)
{
temp=pre[p];
pre[p]=x;
p=temp;
}
return x;
}一道模板题巩固下
下边是检查一个图是否有环。
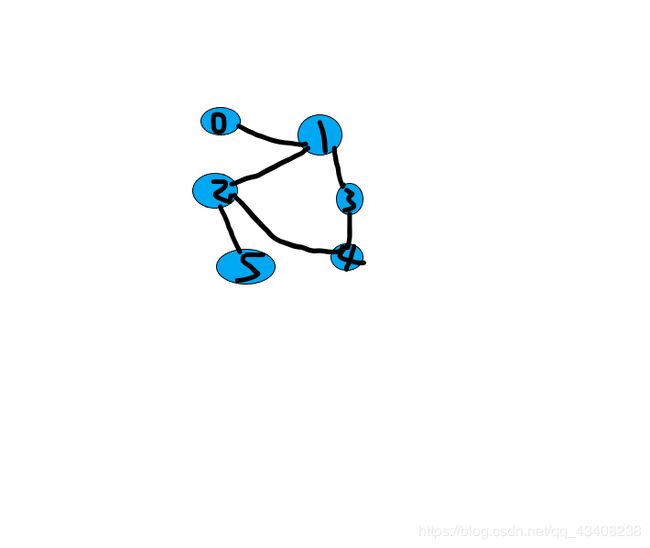
以上图6个顶点,6条边为例
#include
using namespace std;
#define MAX 6//最大顶点数量
int find_root(int x,int parent[])//返回根节点的ID
{
int x_root=x;
while(parent[x_root]!=-1){
x_root=parent[x_root];
}
return x_root;
}
bool union_vertices(int x,int y,int parent[])//1_成功、0_失败
{
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
if(x_root==y_root) return 0;
else {
parent[x_root]=y_root;
return 1;
}
}
int main()
{
int parent[MAX];//
memset(parent,-1,sizeof(parent));//初始化为-1
int edge[6][2]={{0,1},{1,2},{1,3},{2,4},{3,4},{2,5}};//节点的关系
for(int i=0;i<6;++i)
{
int x=edge[i][0];
int y=edge[i][1];
if(union_vertices(x,y,parent)==0){
cout<<"Cycle destected!"<
但是上面的代码有个问题,就是如果连接的节点形如{0,1},{1,2},{2,3},{3,4}...............这样查找的时候会非常慢(eg:把0与10000连在一起)。这时考虑压缩路径。
增加rank数组记录深度,来判断连接两棵树的深度,使得合并后的树的高度越小越好。//按秩合并
#include
using namespace std;
#define MAX 6//最大顶点数量
int find_root(int x,int parent[])//返回根节点的ID
{
int x_root=x;
while(parent[x_root]!=-1){
x_root=parent[x_root];
}
return x_root;
}
bool union_vertices(int x,int y,int parent[],int rank[])//1_成功、0_失败
{
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
if(x_root==y_root) return 0;
else {
//parent[x_root]=y_root;
if(rank[x_root]>rank[y_root])
{
parent[y_root]=x_root;
}
else if(rank[y_root]>rank[x_root]){
parent[x_root]=y_root;
}
else {
parent[x_root]=y_root;
rank[y_root]++;
}
return 1;
}
}
int main()
{
int parent[MAX];//
int rank[MAX];
memset(parent,-1,sizeof(parent));//初始化为-1
memset(rank,0,sizeof(rank));
int edge[6][2]={{0,1},{1,2},{1,3},{2,4},{3,4},{2,5}};//节点的关系
for(int i=0;i<6;++i)
{
int x=edge[i][0];
int y=edge[i][1];
if(union_vertices(x,y,parent,rank)==0){
cout<<"Cycle destected!"< 看,克服心中的恐惧发现其实并不难!
补充:
带边权的并查集。
注:其中数组的含义和并查集Find()与join()的改动要因题而异。下边的只是一道题目(点这)的模板
const int N = 30010;
int d[N];//记录x 与re[x] 之间边的权值
int Size[N];//表示集合的大小
int pre[N];
int Find(int x)
{
if(x == pre[x]) return x;
int root = Find(pre[x]);//递归寻找树根
d[x] += d[pre[x]];//维护d数组——_对边权求和
return pre[x] = root;//路径压缩
}
void join(int x,int y)//y为x的树根
{
x = Find(x) , y = Find(y);
pre[x] = y,d[x] = Size[y];
Size[y] += Size[x];
}