布隆过滤器及常用的字符串哈希算法
布隆过滤器:
说实话看到这个算法我是被惊艳到了,急迫的想学习它
一、问题出现的背景:
假设一亿Email(一个占16字节)约为1.6GB内存,要是几十亿个地址就几百GB,当我们进行类似查询操作时,就要把几百GB装入内存,或者采用负载均衡的分布方法将几百GB分配到几百个计算机中去查询,我们知道hash表的存取时间复杂度都为 O(1),效率十分高。但是占用的内存太大,远远不能解决我们的问题。
那么有没有占用低内存,并且可以满足 O(1) 查询的方法呢,当然是有的,就是大名鼎鼎的布隆过滤器。
二、布隆过滤器的简介:
布隆过滤器(BloomFilter)由一个很长的二进制向量和一系列抗碰撞的Hash函数组成, 可以用于快速判断一个元素是否在一个集合中。其实就是我们嘴上常说的位图的改进。
优点:空间仅由二进制向量决定,并且查询时间远超一般算法(仅需计算k 个Hash函数的值);
缺点:有一定的错误识别率,并且一旦元素被添加到布隆过滤器中就很难再将该元素从布隆过滤器中删除。
三、基本原理:
布隆过滤器是一种多哈希函数映射的快速查找算法。它可以判断出某个元素肯定不在集合里或者可能在集合里,即它不会漏报,但可能会误报。通常应用在一些需要快速判断某个元素是否属于集合,但不严格要求100%正确的场合。
一个空的布隆过滤器是一个m位的位数组,所有位的值都为0。定义了k个不同的符合均匀随机分布的哈希函数,每个函数把集合元素映射到位数组的m位中的某一位。
添加元素:
先把这个元素作为k个哈希函数的输入,拿到k个数组位置,然后把所有的这些位置置为1。查询元素:
把这个元素作为k个哈希函数的输入,得到k个数组位置。这些位置中只要有任意一个是0,元素肯定不在这个集合里。如果元素在集合里,那么这些位置在插入这个元素时都被置为1了。如果这些位置都是1,那么要么元素在集合里,要么所有这些位置是在其他元素插入过程中被偶然置为1了,导致了一次“误报”。一个布隆过滤器的例子见下图,代表了集合{x,y,z}。带颜色的箭头表示了集合中每个元素映射到位数组中的位置。元素w不在集合里,因为它哈希后的比特位置中有一个值为0的位置。在这个图里,m=18,k=3。
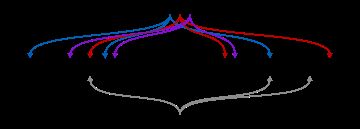
简单的布隆过滤器不支持删除一个元素,因为“漏报”是不允许的。一个元素映射到k位,尽管设置这k位中任意一位为0就能够删除这个元素,但也会导致删除其他可能映射到这个位置的元素。因为没办法决定是否有其他元素也映射到了需要删除的这一位上。
四、算法设计:
首先因为布隆过滤器涉及到位图size的大小,哈希函数的个数,以及误检率三个可变因素,当然误检率完全取决于前两者的设计。从论文中直接把结果给copy过来,记住下面三个公式就可以了:
![]()
其中 p 为误检率,m 为位图的大小,n为样本大小,如果100亿个数据,误检率 0.0001 就可以满足你的要求,将其代入n,p 即可推出位图大小 m 的值。
具体怎么推得我就不推了。接下来说说哈希函数怎么选,是不是看到这觉得字符串哈希函数怎么取也是挺好奇的,我当时看这个的时候痒的不行。
五、字符串哈希函数:
引用该博客:字符串Hash函数对比
/// @brief BKDR Hash Function
/// @detail 本算法由于在Brian Kernighan与Dennis Ritchie的《The C Programming Language》一书被展示而得名,是一种简单快捷的hash算法,也是Java目前采用的字符串的Hash算法(累乘因子为31)。
template<class T>
size_t BKDRHash(const T *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = hash * 131 + ch; // 也可以乘以31、131、1313、13131、131313..
// 有人说将乘法分解为位运算及加减法可以提高效率,如将上式表达为:hash = hash << 7 + hash << 1 + hash + ch;
// 但其实在Intel平台上,CPU内部对二者的处理效率都是差不多的,
// 我分别进行了100亿次的上述两种运算,发现二者时间差距基本为0(如果是Debug版,分解成位运算后的耗时还要高1/3);
// 在ARM这类RISC系统上没有测试过,由于ARM内部使用Booth's Algorithm来模拟32位整数乘法运算,它的效率与乘数有关:
// 当乘数8-31位都为1或0时,需要1个时钟周期
// 当乘数16-31位都为1或0时,需要2个时钟周期
// 当乘数24-31位都为1或0时,需要3个时钟周期
// 否则,需要4个时钟周期
// 因此,虽然我没有实际测试,但是我依然认为二者效率上差别不大
}
return hash;
}
/// @brief SDBM Hash Function
/// @detail 本算法是由于在开源项目SDBM(一种简单的数据库引擎)中被应用而得名,它与BKDRHash思想一致,只是种子不同而已。
template<class T>
size_t SDBMHash(const T *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = 65599 * hash + ch;
//hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;
}
return hash;
}
/// @brief RS Hash Function
/// @detail 因Robert Sedgwicks在其《Algorithms in C》一书中展示而得名。
template<class T>
size_t RSHash(const T *str)
{
register size_t hash = 0;
size_t magic = 63689;
while (size_t ch = (size_t)*str++)
{
hash = hash * magic + ch;
magic *= 378551;
}
return hash;
}
/// @brief AP Hash Function
/// @detail 由Arash Partow发明的一种hash算法。
template<class T>
size_t APHash(const T *str)
{
register size_t hash = 0;
size_t ch;
for (long i = 0; ch = (size_t)*str++; i++)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
/// @brief JS Hash Function
/// 由Justin Sobel发明的一种hash算法。
template<class T>
size_t JSHash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 1315423911;
while (size_t ch = (size_t)*str++)
{
hash ^= ((hash << 5) + ch + (hash >> 2));
}
return hash;
}
/// @brief DEK Function
/// @detail 本算法是由于Donald E. Knuth在《Art Of Computer Programming Volume 3》中展示而得名。
template<class T>
size_t DEKHash(const T* str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 1315423911;
while (size_t ch = (size_t)*str++)
{
hash = ((hash << 5) ^ (hash >> 27)) ^ ch;
}
return hash;
}
/// @brief FNV Hash Function
/// @detail Unix system系统中使用的一种著名hash算法,后来微软也在其hash_map中实现。
template<class T>
size_t FNVHash(const T* str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 2166136261;
while (size_t ch = (size_t)*str++)
{
hash *= 16777619;
hash ^= ch;
}
return hash;
}
/// @brief DJB Hash Function
/// @detail 由Daniel J. Bernstein教授发明的一种hash算法。
template<class T>
size_t DJBHash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 5381;
while (size_t ch = (size_t)*str++)
{
hash += (hash << 5) + ch;
}
return hash;
}
/// @brief DJB Hash Function 2
/// @detail 由Daniel J. Bernstein 发明的另一种hash算法。
template<class T>
size_t DJB2Hash(const T *str)
{
if(!*str) // 这是由本人添加,以保证空字符串返回哈希值0
return 0;
register size_t hash = 5381;
while (size_t ch = (size_t)*str++)
{
hash = hash * 33 ^ ch;
}
return hash;
}
/// @brief PJW Hash Function
/// @detail 本算法是基于AT&T贝尔实验室的Peter J. Weinberger的论文而发明的一种hash算法。
template<class T>
size_t PJWHash(const T *str)
{
static const size_t TotalBits = sizeof(size_t) * 8;
static const size_t ThreeQuarters = (TotalBits * 3) / 4;
static const size_t OneEighth = TotalBits / 8;
static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);
register size_t hash = 0;
size_t magic = 0;
while (size_t ch = (size_t)*str++)
{
hash = (hash << OneEighth) + ch;
if ((magic = hash & HighBits) != 0)
{
hash = ((hash ^ (magic >> ThreeQuarters)) & (~HighBits));
}
}
return hash;
}
/// @brief ELF Hash Function
/// @detail 由于在Unix的Extended Library Function被附带而得名的一种hash算法,它其实就是PJW Hash的变形。
template<class T>
size_t ELFHash(const T *str)
{
static const size_t TotalBits = sizeof(size_t) * 8;
static const size_t ThreeQuarters = (TotalBits * 3) / 4;
static const size_t OneEighth = TotalBits / 8;
static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);
register size_t hash = 0;
size_t magic = 0;
while (size_t ch = (size_t)*str++)
{
hash = (hash << OneEighth) + ch;
if ((magic = hash & HighBits) != 0)
{
hash ^= (magic >> ThreeQuarters);
hash &= ~magic;
}
}
return hash;
}
具体的一些测试结果看原文吧。
六、直接上code:
BloomFilter.h
#pragma once
#includeBitMao.h
#pragma once
#includeBitMap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"BitMap.h"
#includeBloomFilter.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"BloomFilter.h"
#include"BitMap.h"
#include七、总结:
布隆过滤器优点:
- 存储空间和插入/查询时间都是常数,远远超过一般的算法
- Hash函数之间相互独立,方便由硬件并行实现
- 不需要存储元素本身,在某些对保密要求非常严格的场合有优势
布隆过滤器缺点:
- 有一定的误识别率
- 删除困难