多分类器:KNN,SVM,Softmax,2-Layer-Affine-Net(以图像分类为例子)
多分类器:KNN,SVM,Softmax,2-Layer-Affine-Net(以图像分类为例子)
记录一下 CS 231N 计算机视觉这门课所提到的一些基础分类器,结合机器学习中学到的二元分类器算法,并以 CIFAR 10 作为训练集测试多分类器性能。
KNN K近邻分类
主要思路:寻找训练集到测试集中最相似的 k k k 个图像(距离由矩阵二范数、或是 F r o b i n u s Frobinus Frobinus 范数表示),并由 k k k 个最优结果投票决定其标签。
算法流程:
- 训练集导入 X X X 与标签 y y y
- 测试集输入 x ^ \hat x x^ ,找到 X X X 中与 x ^ \hat x x^ 距离最近的 k k k 个图像: χ = { X ~ 1 , ⋯ , X ~ k } \chi = \{\tilde X_1,\cdots, \tilde X_k\} χ={X~1,⋯,X~k} (一般用二范数距离)
- 对标签进行计数: η = { ( X ~ 1 , y ~ ( 1 ) ) , ⋯ , ( X ~ k , y ~ ( p ) ) } \eta = \{(\tilde X_1, \tilde y^{(1)}),\cdots, (\tilde X_k, \tilde y^{(p)})\} η={(X~1,y~(1)),⋯,(X~k,y~(p))}
- 找到 η \eta η 中出现次数最多的 y ~ ( i ) \tilde y^{(i)} y~(i) ,即为这次分类的结果。
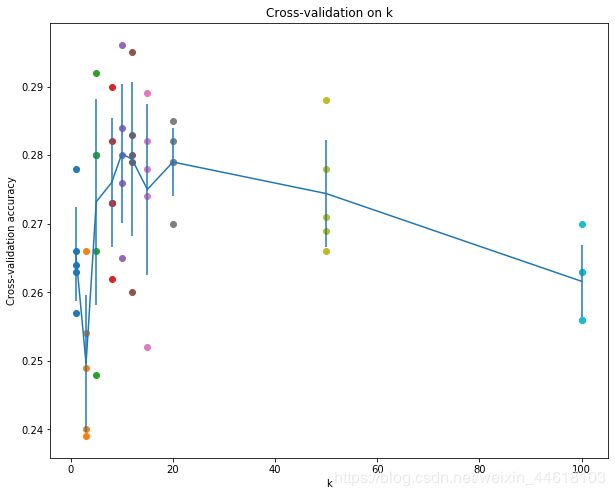
**图像分类结果:**对 C I F A R − 10 CIFAR-10 CIFAR−10 这个数据集上选取不同 k k k 值进行五折 J a c k k n i f e Jackknife Jackknife 交叉验证总体准确度在 27 % 27\% 27% 左右。
SVM 支持向量机
支持向量机依赖于凸集分离定理,即:两个不相交凸集之间可以用超平面分离。但训练集中的数据通常不是凸集。
二元支持向量机
二元支持向量机的最优化问题的拉格朗日函数为:(最后为正则项)
L ( w , b , a ) = 1 2 ∥ w ∥ 2 − 1 2 ∑ i N a i y i ( w T x i − b ) + ∑ i a i L(w, b, a)=\frac{1}{2}\|w\|^2-\frac{1}{2}\sum_i^N a_iy_i(w^Tx_i-b)+\sum_i a_i L(w,b,a)=21∥w∥2−21i∑Naiyi(wTxi−b)+i∑ai
最优化如上函数,得到最优解 w w w 。这里的 w w w 可以单位化为 w = w ∥ w ∥ w=\frac{w}{\|w\|} w=∥w∥w ,实际上等价于:
L ( w , b , a ) = − 1 2 ∑ i N a i y i ( w T x i − b ) + ∑ i a i L(w, b, a)=-\frac{1}{2}\sum_i^N a_iy_i(w^Tx_i-b)+\sum_i a_i L(w,b,a)=−21i∑Naiyi(wTxi−b)+i∑ai
多元支持向量机
多元支持向量机相当于每个第 i i i 类与非 i i i 类之间进行支持向量机的划分。假设总供 m m m 个组别,则在多分类问题中,相当于建立了 m m m 个互相独立的支持向量机模型。 W ∈ R m ∗ n W\in \R^{m*n} W∈Rm∗n 为一个权重矩阵, W x , x ∈ R n Wx,x\in \R^n Wx,x∈Rn 内积输出的结果为一个向量,分别表示对每个类别的评分。
N N N 元支持向量机对训练集的一个元素 x i x_i xi 的损失函数为:( j j j 代表类别, s j s_j sj 表示对第 j j j 个组别上的评分, s y i s_{y_i} syi 表示训练集在第 j j j 个支持向量机空间内的标签 ( − 1 -1 −1 or 1 1 1))即表明这一分类在不属于第 y i y_i yi 个分类的支持向量机空间下的重错分的分数。
L i = ∑ j ≠ y i max ( 0 , s j − s y i + 1 ) L_i = \sum_{j\ne y_i}\max(0, s_j-s_{y_i}+1) Li=j=yi∑max(0,sj−syi+1)
整个损失函数为:(这里省略正则项,也省略了惩罚项的系数)这里的损失函数实际上也可以定义为 max ( 0 , s j − s y i + 1 ) 2 \max(0, s_j-s_{y_i}+1)^2 max(0,sj−syi+1)2 ,取决于对误差的容忍性。
L = ∑ i L i = ∑ i ∑ j ≠ y i max ( 0 , s j − s y i + 1 ) L=\sum_{i}L_i = \sum_i\sum_{j\ne y_i}\max(0, s_j-s_{y_i}+1) L=i∑Li=i∑j=yi∑max(0,sj−syi+1)
如果分类正确, s j − s y i + 1 < 0 s_j-s_{y_i}+1<0 sj−syi+1<0 整个损失函数就为 0 0 0 ,如果全部分类均不正确,则损失函数理论上能够达到正无穷。
交叉验证结果分析:准确率 0.379000,较 K N N KNN KNN 来说有更好的泛化能力。权重矩阵比较模糊。
Softmax 分类器
又称(多分类逻辑回归模型)。对于二元逻辑回归问题,对于一个输入给出的输出 y ^ \hat y y^ 是一个概率。
Y ^ = exp ( w T x ) 1 + exp ( w T x ) ∈ [ 0 , 1 ) \hat Y = \frac{\exp(w^Tx)}{1+\exp(w^Tx)}\in [0, 1) Y^=1+exp(wTx)exp(wTx)∈[0,1)
在二元逻辑回归中,实际上这个函数可以写为:
Y ^ = exp ( w T x ) exp ( 0 ) + exp ( w T x ) ∈ [ 0 , 1 ) \hat Y = \frac{\exp(w^Tx)}{\exp(0)+\exp(w^Tx)}\in [0, 1) Y^=exp(0)+exp(wTx)exp(wTx)∈[0,1)
实际上 exp ( 0 ) exp ( 0 ) + e x p ( w T x ) \frac{\exp(0)}{\exp(0)+exp(w^Tx)} exp(0)+exp(wTx)exp(0) 是取 0 0 0 的概率,而原本输出的 Y ^ \hat Y Y^ 表示属于 1 1 1 类的概率,这个函数具有非常好的二元性。将其扩展到所有 m m m 个类别,输出是一个 m m m 维向量,因此公式如下:
P ( Y = k ∣ X = x i ) = exp ( W x i ) ∑ j m exp ( ( W x i ) j ) ∈ R m P(Y=k|X=x_i)=\frac{\exp(Wx_i)}{\sum_j^m \exp((Wx_i)_j)}\in \R^{m} P(Y=k∣X=xi)=∑jmexp((Wxi)j)exp(Wxi)∈Rm
与二元逻辑回归的损失函数相同,多分类逻辑回归的损失函数如果用最小二乘定义的话,会是一个非凸的函数,不利于求解。这里使用的是最大似然估计的方法:
L i = − log P ( Y = y i ∣ X = x i ) L_i=-\log P(Y=y_i|X=x_i) Li=−logP(Y=yi∣X=xi)
十折交叉验证准确率:
lr 1.000000e-07 reg 2.500000e+04 train accuracy: 0.348837 val accuracy: 0.365000
lr 1.000000e-07 reg 5.000000e+04 train accuracy: 0.330980 val accuracy: 0.342000
lr 5.000000e-07 reg 2.500000e+04 train accuracy: 0.349531 val accuracy: 0.363000
lr 5.000000e-07 reg 5.000000e+04 train accuracy: 0.333429 val accuracy: 0.351000
best validation accuracy achieved during cross-validation: 0.365000
图像上来说,这个权重矩阵好像比 S V M SVM SVM 更清晰一点。
Two Layer Affine Network
神经网络的主要基础就是 求解梯度的链式法则: ∂ f ( g ( x ) ) ∂ x = ∂ f ∂ g ∂ g ∂ x \frac{\partial f(g(x))}{\partial x}=\frac{\partial f}{\partial g}\frac{\partial g}{\partial x} ∂x∂f(g(x))=∂g∂f∂x∂g,以及向量值函数的梯度的求解。
z ← f ( . ) { g 1 g 2 ⋮ g n where: each g i ( . ) { x 1 x 2 ⋮ x n z\leftarrow f(.)\begin{cases}g_1\\g_2\\\vdots\\g_n\end{cases}\text{where: each } g_i(.)\begin{cases}x_1\\x_2\\\vdots\\x_n\end{cases} z←f(.)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧g1g2⋮gnwhere: each gi(.)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x1x2⋮xn
对于向量值函数的求导 ∂ g ∂ x \frac{\partial g}{\partial x} ∂x∂g,我们最后得到的结果是一个 J a c o b Jacob Jacob 矩阵,我在 凸优化 [1]:梯度与次梯度 这篇文章中写过。将整个 J a c o b Jacob Jacob 矩阵记为 ∂ g ∂ x = J \frac{\partial g}{\partial x} = J ∂x∂g=J 。在这里最后总的梯度是 J J J 与 ∂ f ∂ g = ∇ \frac{\partial f}{\partial g}=\nabla ∂g∂f=∇ 的内积: ∂ f ∂ x = J × ∇ \frac{\partial f}{\partial x}=J\times \nabla ∂x∂f=J×∇ 。
单层神经网络如支持向量机中的打分方式一样: f = W x f=Wx f=Wx,而双层神经网络如下:
f = W 2 max ( 0 , W 1 x ) f=W_2\max(0, W_1x) f=W2max(0,W1x)
这里对应的 max \max max 针对每一个元素。、一般来说,如果两层的神经网络都是线性的,则最终这个神经网络的输出结果也是线性的(第二层相当于对第一层神经网络进行一个降秩操作),相当于一层神经网络。
这里用的是由两个仿射变换构成神经网络。分别为 y 1 = W 1 x + b 1 y_1 =W_1x+b_1 y1=W1x+b1 这是第一层神经网络, y 2 = W 2 y 1 + b 2 y_2 = W_2y_1+b_2 y2=W2y1+b2 这是第二层神经网络。其中 W 1 , W 2 W_1,W_2 W1,W2 全部初始化为服从正态分布的随机数构成的矩阵。
这里损失函数用 s o f t m a x softmax softmax 函数来定义:(这里加上正则化)
z = W 2 max ( 0 , W 1 x + b 1 ) + b 2 L ( W 1 , W 2 , b 1 , b 2 ) = 1 N log ( s o f t m a x ( z ) ) + α ( ∥ W 1 ∥ F r o 2 + ∥ W 2 ∥ F r o 2 ) \begin{aligned}z &= W_2\max(0, W_1 x+b_1)+b_2\\L(W_1,W_2,b_1,b_2)&=\frac{1}{N}\log (softmax(z))+\alpha(\|W_1\|_{Fro}^2+\|W_2\|_{Fro}^2)\end{aligned} zL(W1,W2,b1,b2)=W2max(0,W1x+b1)+b2=N1log(softmax(z))+α(∥W1∥Fro2+∥W2∥Fro2)
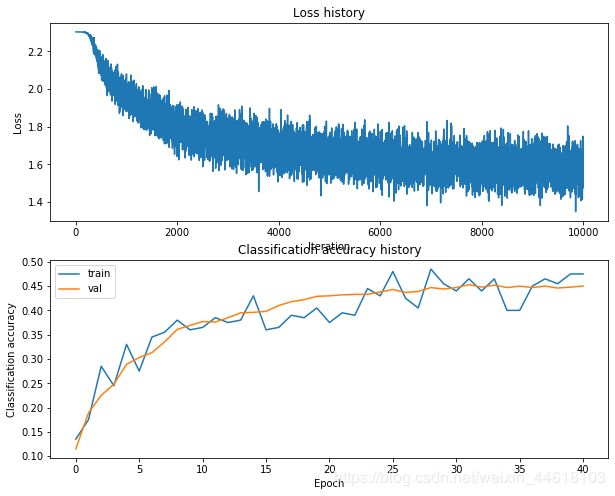
下降方法:对上式求导,进行随机梯度下降法。第一张图是损失函数,第二张图是准确率
算法中 W 1 W_1 W1 权重矩阵的可视化模型( W 1 W_1 W1 有 50 50 50 行)。
如上线性神经网络的分类精确率提高的原因初步猜测是:
- 每个分类下都有若干张图(也就是最后一层神经网络的行数),相当于一个由若干个支持向量机组成的集成学习
- 在集成学习中,每个分类器都进行投票(也就是最后我们得到的 f = W 2 z + b 2 f=W_2z+b_2 f=W2z+b2 这一步),从而能够达到更好的分类精确度。