2019牛客暑期多校训练营（第七场）E

Find the median

动态去寻找一个序列的中位数；但是此题没有要求在线，于是可以离线操作。由于L,R
都比较大，需要离散化。

 寻找中位数，那么数量上可定具有单调性，所以可以考虑二分去找。刚开始想用树状数组去维护的数量，然后二分的。然后写着写着就发现不对了，开了一个树状数组去记录每个区间以左端点为起点的数量大小，可是考虑一个问题，有的区间比较大，完全可能在树状数组上跨越了多个节点，相当于覆盖了多个节点，也就说是这些信息彼此是交叉的，难以维护。之后觉得写不了，改用线段树去维护，可是对于非叶子可以维护，而对于叶子节点我就无能为力了。哎，无奈又放弃了。

2019牛客暑期多校训练营（第七场）E Governing sand【树状数组+离散化】【二分】
  看了这篇博客，又燃起了树状数组的希望。毕竟树状数组这东西好写啊。能用树状数组的打死不用线段树（就是这么皮），鉴于之前的顾虑，这次换个角度去维护数量，开两个树状数组，

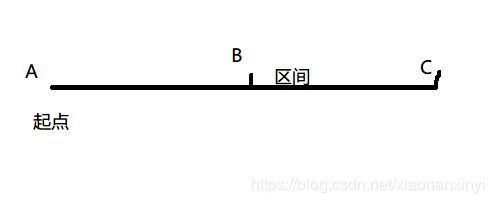
假如要求BC之间的数量，那我们是不是可以用AC-AB，同理，对于给的区间我们也这样去维护，bit1维护AC的信息，bit2维护AB之间的信息，对于AC来说，因为起点都一样所以记录右端点的数量即可，而对于bit2,为了区间之间不相互影响所以要记录他在哪里结束。
感觉说得有点乱，但是大概就是这个思路，具体可以参看代码；

之后二分的时候，为了使我们查询的位置符合条件，

 upper_bound(a+1,a+1+len,mid)-a-1;

先找到第一个大于它的数再减1，就能保证是符合条件的；
为什这样用呢

lower_bound(a + 1, a + 1 + len, x) - a

这里返回的是大于等于，如果返回的数是等于的话，那么ok没问题。可是如果返回的是大于，那么就会导致我多统计了。如果减1，那么当返回结果是等于的时候又会导致少统计了。
于是用upper_bound()就很ok。

AC_CODE

#include
using namespace  std;
#define ll long long
const int N = 1000 * 100 * 8 + 10;
ll X1, X2, A1, B1, C1, M1;
ll Y1, Y2, A2, B2, C2, M2;
ll n, X, Y, L[N], R[N];
ll a[N], len;

int getid(int x) {
	return lower_bound(a + 1, a + 1 + len, x) - a;
}

struct {
	ll s[N];
	void init() { for (int i = 0; i <= len; i++)s[i] = 0;}
	int lowerbit(int x) { return x & -x; }
	void add(int x, ll k) { while (x <= len)s[x] += k, x += lowerbit(x); }
	ll query(ll x) { ll ans = 0; while (x)ans += s[x],x-=lowerbit(x); return ans;}
}bit1,bit2;

int main() {
	scanf("%lld", &n);
	scanf("%lld%lld%lld%lld%lld%lld", &X1, &X2, &A1, &B1, &C1, &M1);
	scanf("%lld%lld%lld%lld%lld%lld", &Y1, &Y2, &A2, &B2, &C2, &M2);
	L[1] = min(X1, Y1) + 1; L[2] = min(X2, Y2) + 1;
	R[1] = max(X1, Y1) + 2; R[2] = max(X2, Y2) + 2;

	for (int i = 3; i <= n; i++) {
		X = (A1*X2 + B1 * X1 + C1) % M1;
		Y = (A2*Y2 + B2 * Y1 + C2) % M2;
		L[i] = min(X, Y) + 1;
		R[i] = max(X, Y) + 2;
		X1 = X2; X2 = X;
		Y1 = Y2; Y2 = Y;
	}
	int cnt = 1;
	for (int i = 1; i <= n; i++)a[cnt++] = L[i], a[cnt++] = R[i];
	sort(a + 1, a + cnt);
	len = unique(a + 1, a + cnt) - a;
	len--;
	ll sum = 0;
	bit1.init(); bit2.init();
	for (int i = 1; i <= n; i++) {
		sum += R[i] - L[i];
		int l = getid(L[i]), r=getid(R[i]);
		bit1.add(l, 1); bit1.add(r, -1);
		bit2.add(l, -L[i]+1); bit2.add(r,R[i]-1);
		int left = 0, right = 1e9;
		while (left < right) {
			int mid = left + right >> 1;
			int k = upper_bound(a+1,a+1+len,mid)-a-1;
			ll tem = bit1.query(k)*mid + bit2.query(k);
			if (tem < (sum + 1) / 2)left = mid+1;
			else right = mid;
		}
		printf("%d\n",right);
	}
	return 0;
}