深度学习——感知机：多层感知机（multi-layered perceptron）图文详解

一，多层感知机

  在上一篇深度学习——感知机（perceptron）图文详解中我们已经讨论完了简单感知机的原理和实现了，同时也知道了简单感知机的局限性了，不能表示异或门这点让人深感遗憾。今天我们就将介绍多层感知机，它可以通过“叠加层”来表示异或门。不过，我们先暂时不考虑叠加层具体是指什么，先从其他视角来思考一下异或门的问题

1.1 现在已有的门电路组合

  异或门的制作方法有很多，其中之一就是组合我们前面做好的与门、与非门、或门进行配置。这里，与门、与非门、或门用图1中的符号表示。

图1
  另外，图1中与非门前端的○表示反转输出的意思。那么，如果要实现异或门的话，需要如何配置与门、与非门和或门呢？是不是用与门、与非门、或门代替图2中的各个“？”，就可以实现异或门。
图2
  我们前面讲到的感知机的局限性，严格地讲，应该是“单层感知机无法表示异或门”或者“单层感知机无法分离非线性空间”。不过接下来我们就将看到通过组合感知机（叠加层）就可以实现异或门了。
  异或门可以通过图3所示的配置来实现。这里， x1和x2表示输入信号，y表示输出信号。 x1和x2是与非门和或门的输入，而与非门和或门的输出则是与门的输入。
图3
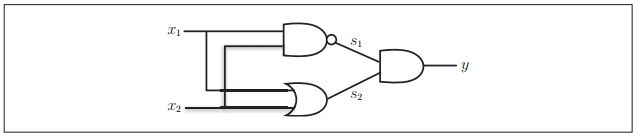
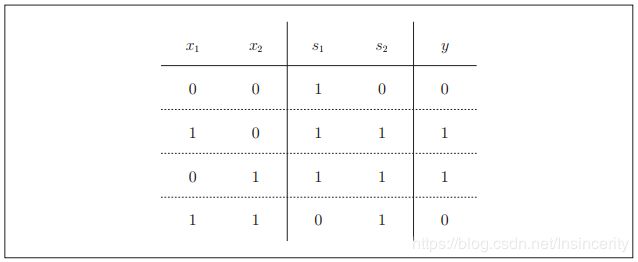
  现在，我们来确认一下图3的配置是否真正实现了异或门。这里，把s1作为与非门的输出，把s2作为或门的输出，填入真值表中。结果如图4所示，观察x1、 x2、 y，可以发现确实符合异或门的输出。
图4 异或门的真值表

1.2 异或门的实现

  下面我们试着用Python来实现图3所示的异或门。使用之前定义的AND函数、 NAND函数、 OR函数，可以像下面这样的实现。

def XOR(x1, x2):
	s1 = NAND(x1, x2)
	s2 = OR(x1, x2)
	y = AND(s1, s2)
	return y

这个XOR函数会输出预期的结果。

XOR(0, 0) # 输出0
XOR(1, 0) # 输出1
XOR(0, 1) # 输出1
XOR(1, 1) # 输出0

  这样，异或门的实现就完成了。下面我们试着用感知机的表示方法（明确地显示神经元）来表示这个异或门，结果如图5所示。如图5，异或门是一种多层结构的神经网络。这里，将最左边的一列称为第0层，中间的一列称为第1层，最右边的一列称为第2层。图5的感知机与前面介绍的与门、或门的感知机（上一篇中的图1）形状不同。实际上，与门、或门是单层感知机，而异或门是2层感知机。叠加了多层的感知机也称为多层感知机（multi-layered perceptron）。

图5 感知机表示异或门
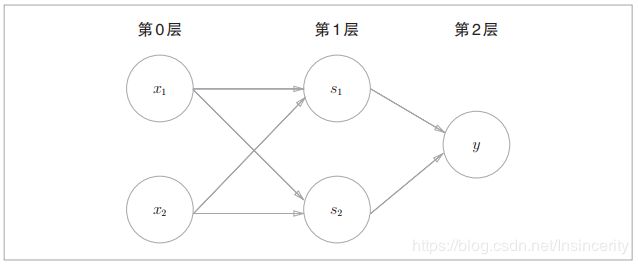
  图5中的感知机总共由3层构成，但是因为拥有权重的层实质上只有2层（第0层和第1层之间，第1层和第2层之间），所以称为“2层感知机”。不过，也有的文献认为图5的感知机是由3层构成的，因而将其称为“3层感知机”。
  在图5所示的2层感知机中，先在第0层和第1层的神经元之间进行信号的传送和接收，然后在第1层和第2层之间进行信号的传送和接收，具体如下所示。
1.第0层的两个神经元接收输入信号，并将信号发送至第1层的神经元。
2.第1层的神经元将信号发送至第2层的神经元，第2层的神经元输出y。
  这种2层感知机的运行过程可以比作流水线的组装作业。第1段（第1层）的工人对传送过来的零件进行加工，完成后再传送给第2段（第2层）的工人。第2层的工人对第1层的工人传过来的零件进行加工，完成这个零件后出货（输出）。
  像这样，在异或门的感知机中，工人之间不断进行零件的传送。通过这样的结构（2层结构），感知机得以实现异或门。这可以解释为“单层感知机无法表示的东西，通过增加一层就可以解决”。也就是说，通过叠加层（加深层），感知机能进行更加灵活的表示。

二，从与非门到计算机

  多层感知机可以实现比之前见到的电路更复杂的电路。比如，进行加法运算的加法器也可以用感知机实现。此外，将二进制转换为十进制的编码器、满足某些条件就输出1的电路（用于等价检验的电路）等也可以用感知机表示。实际上，使用感知机是可以表示计算机的。计算机是处理信息的机器。向计算机中输入一些信息后，它会按照某种既定的方法进行处理，然后输出结果。所谓“按照某种既定的方法进行处理”是指，计算机和感知机一样，也有输入和输出，会按照某个既定的规则进行计算。人们一般会认为计算机内部进行的处理非常复杂，而实际上只需要通过与非门的组合，就能再现计算机进行的处理。这说明了什么？说明使用感知机也可以表示计算机。前面也介绍了，与非门可以使用感知机实现。也就是说，如果通过组合与非门可以实现计算机的话，那么通过组合感知机也可以表示计算机（感知机的组合可以通过叠加了多层的单层感知机来表示）。
  综上，多层感知机能够进行复杂的表示，甚至可以构建计算机。那么，什么构造的感知机才能表示计算机呢？层级多深才可以构建计算机呢？理论上可以说2层感知机就能构建计算机。这是因为，已有研究证明，2层感知机（严格地说是激活函数使用了非线性的sigmoid函数的感知机）可以表示任意函数。但是，使用2层感知机的构造，通过设定合适的权重来构建计算机是一件非常累人的事情。实际上，在用与非门等低层的元件构建计算机的情况下，分阶段地制作所需的零件（模块）会比较自然，即先实现与门和或门，然后实现半加器和全加器，接着实现算数逻辑单元（ALU），然后实现CPU。因此，通过感知机表示计算机时，使用叠加了多层的构造来实现是比较自然的流程。

三，总结

• 感知机是具有输入和输出的算法。给定一个输入后，将输出一个既定的值。
• 感知机将权重和偏置设定为参数。
• 使用感知机可以表示与门和或门等逻辑电路。
• 异或门无法通过单层感知机来表示。
• 使用2层感知机可以表示异或门。
• 单层感知机只能表示线性空间，而多层感知机可以表示非线性空间。
• 多层感知机（在理论上）可以表示计算机。
  结合上一篇，我们学习了感知机。感知机是一种非常简单的算法，要理解它的构造并不难，不过因为感知机是学习的神经网络的基础，因此弄明白感知机是非常重要的。