用堆处理大数据量的topN问题和排序问题

一般来说，涉及到topN类的问题时，我们首先想到的是采用分治法：先随机取一个数其他数与它比较，如果前一部分总数大于100个（这里架设找出前100条），那就继续在前一部分进行partition寻找；如果前一部分的数小于100个，那就在后一部分再进行partition。

然而当数据量大的时候，需要初始化加载全部数据，空间复杂度会特别大。或者将数据分步读入，分开进行partition再合并，但是这样操作又增加了磁盘的读写操作，效率受到影响。

这时候，我们可以考虑采用小顶堆的思想，在内存中维护一个100大小的小顶堆，然后每次读取一个数与堆顶进行比较，若比堆顶大，则把堆顶弹出，把当前数据压入堆顶，然后调整小顶堆，把数据从堆顶下移到一定位置即可，最终得到的小顶堆即为最大的100条数据。（我们可以将整个过程想象成一场挑战赛，战场中有100位英雄，剩下所有人依次挑战，每次选100人中的最弱的一个挑战，胜了则取代它，最终战场中留下的一定是最强的100个）

（相反如果要找最小前N个数可用大顶堆思想）同理可比作“每次选100人中的最强的一个挑战，输了则取代它，最终战场中留下的一定是最弱鸡的100个“

堆的概念

构建堆的基础是必须满足完全二叉树的结构，满足完全二叉树有两个条件：

从作为第一层的根开始，除了最后一层之外，第N层的元素个数都必须是2的N次方；第一层2个元素，第二层4个，第三层8个，以此类推。
而最后一行的元素，都要紧贴在左边，换句话说，每一行的元素都从最左边开始安放，两个元素之间不能有空闲。

具备了这两个特点的树，就是一棵完全二叉树 ，接下来再看堆的概念，堆分大根堆和小根堆：

大根堆：根结点的键值是所有堆结点键值中最大者（不仅大于其子节点，同时大于堆中的所有节点值）。每个节点的值都>=其左右孩子（如果有的话）值的完全二叉树。

小根堆：根结点的键值是所有堆结点键值中最小者（同理）。每个节点的值都<=其左右孩子值的完全二叉树。

我们用公式可以概括为：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

如下图即为调整好的大根堆和小根堆：

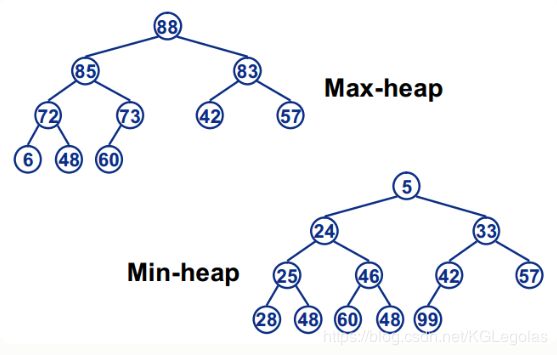
以下构建过程的内容参考自：https://www.cnblogs.com/chengxiao/p/6129630.html

堆的构建过程

下面我们通过图例讲解来认识将无序序列构造成一个大顶堆的过程：

1.假设给定无序序列结构如下：

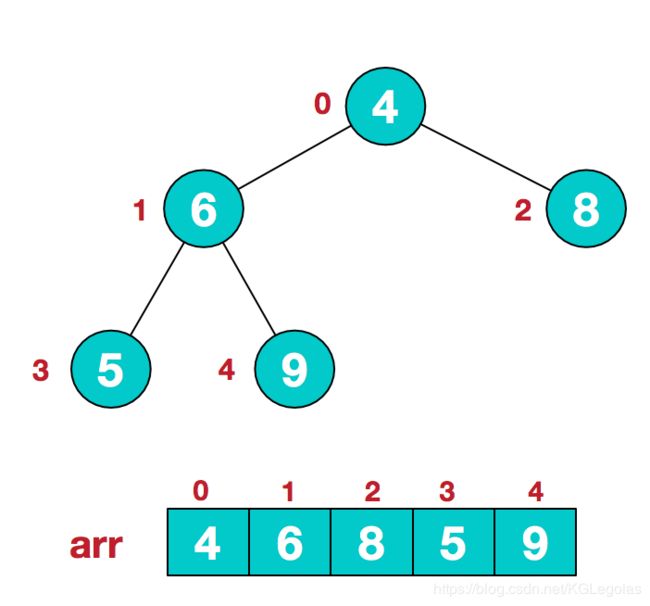
2.我们构建堆时，从最后一个非叶结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

完成6与子节点的调整之后，需要重新考量调整到的6位置的9作为根节点的那棵子树的两个子节点，是否还满足大根堆的原则（这里因为其是叶子节点，所以不加考虑，但是一定要时刻有这种思维）每一次交换，都必须要循环把子树部分判别清楚。

3.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换

4,9交换之后，判断9的双子节点是否满足大根堆原则，这时发现子根[4,5,6]发生了结构混乱，所以继续调整

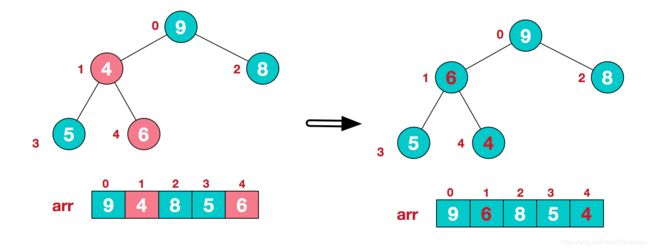
此时，我们构造了一个大顶堆，至此我们将要筛选的数据依次与堆顶比较，若比堆顶小，则替换堆顶，然后重新调整大顶堆，如此循环最终堆里的元素就是所有数据里最小的N条。

堆的排序过程

我们对建好的堆的排序，其实就是如下的一个循环操作：

for (int j = heap.length - 1; j > 0; j–) {
1.堆首和堆尾的元素进行交换
2.对前j个元素的堆进行重排
}

小根堆的实现和排序

首先我们定义节点方法：

 // 父节点
    private int parent(int n) {
        return (n - 1) / 2;
    }

    // 左孩子
    private int left(int n) {
        return 2 * n + 1;
    }

    // 右孩子
    private int right(int n) {
        return 2 * n + 2;
    }

    void swap(int[] arr, int a, int b) {
        arr[a] = arr[a] ^ arr[b];
        arr[b] = arr[a] ^ arr[b];
        arr[a] = arr[a] ^ arr[b];
    }

然后我们给定一个无序数组构建一个小根堆：

private void buildMinHeap(int[] data) {
       //从根的第一个子节点开始遍历完整个数组
        for (int i = 1; i < data.length; i++) {
            int t = i;
            //从节点i不断向根节点遍历，若不满足最小堆条件则调整堆
            while (t != 0 && data[parent(t)] > data[t]) {
                swap(data, t, parent(t));
                t = parent(t);
            }
        }
    }

小根堆构建完成之后，开始对其进行排序操作：我们调整小根堆的时候每次从根节点开始，如果根节点大于子节点，则进行置换操作，且对于小根堆，我们置换左右节点中的更小的那一个，对于置换的子节点，被当作新的根节点进行新一轮的循环判断。（大根堆的调整逻辑与小根堆正好相反）

  public void sortMinHeap(int[] heap) {
        // 开始排序逻辑
        for (int j = heap.length - 1; j > 0; j--) {
            swap(heap, 0, j);//将堆顶元素与末尾元素进行交换
            int i = 0;
            //从根节点开始，如果根节点大于子节点，循环进行置换操作
            while ((left(i) < j && heap[i] > heap[left(i)])
                    || (right(i) < j && heap[i] > heap[right(i)])) {
                if (right(i) < j && heap[right(i)] < heap[left(i)]) {
                    // 右孩子更小，置换右孩子（总之与两者中更小的置换）
                    swap(heap, i, right(i));
                    i = right(i);
                } else {
                    // 否则置换左孩子
                    swap(heap, i, left(i));
                    i = left(i);
                }
            }
        }
    }

下面调用我们定义好的方法进行测试：

HeapSort heapSort = new HeapSort();
int[] arr1 = new int[]{56, 30, 71, 18, 29, 93, 44, 75, 20, 65}

heapSort.buildMinHeap(arr1);
System.out.println("构建的最小堆：");
System.out.println(Arrays.toString(arr1));

heapSort.sortMinHeap(arr1);
System.out.println("排序的最小堆：");
System.out.println(Arrays.toString(arr1));

测试输出如下：

构建的最小堆：
[18, 20, 44, 29, 30, 93, 71, 75, 56, 65]
排序的最小堆：
[93, 75, 71, 65, 56, 44, 30, 29, 20, 18]

利用小根堆解决TopN问题

上面，基于我们建好的小根堆，可以将需要筛选的元素依次与堆顶元素进行比较，若比堆顶大，则置换堆顶，然后对堆进行调整，最终，我们可以得到序列中前N条最大的记录。

我们定义adjustMinHeap方法temp为要与堆顶比较的元素，heap为我们建好的小根堆：

 private void adjustMinHeap(int temp, int[] heap) {
        int len = heap.length;
        if (temp <= heap[0]) {
            return;
        }
        //如果该数比堆顶大则置换堆顶
        heap[0] = temp;
        // 调整堆顶
        int i = 0;
        while ((left(i) < len && heap[i] > heap[left(i)])
                || (right(i) < len && heap[i] > heap[right(i)])) {
            if (right(i) < len && heap[right(i)] < heap[left(i)]) {
                // 右孩子更小，置换右孩子
                swap(heap, i, right(i));
                i = right(i);
            } else {
                // 否则置换左孩子
                swap(heap, i, left(i));
                i = left(i);
            }
        }
    }

然后定义findTopN方法，在该方法中对要筛选的数据进行循环比较。

 public void findTopN(int n, int[] heap, int[] data) {
        // n往后的数进行调整
        for (int i = n; i < data.length; i++) {
            adjustMinHeap(data[i], heap);
        }
    }

下面进行测试：

 HeapSort heapSort = new HeapSort();
    int[] arr1 = new int[]{56, 30, 71, 18, 29, 93, 44, 75, 20, 65, 68, 34, 30, 23, 45, 67, 84, 234, 676, 43, 75, 35, 675, 75, 33};
    int heapLen = 10;
    //我们先取前10个元素构建一个最小堆
    int[] heap = Arrays.copyOf(arr1, heapLen);
    heapSort.buildMinHeap(heap);
    System.out.println("构建的最小堆：");
    System.out.println(Arrays.toString(heap));

    //然后调用findTopN方法去循环遍历调整堆
    heapSort.findTopN(heapLen, heap, arr1);
    System.out.println("调整后数组：");
    System.out.println(Arrays.toString(heap));

测试输出如下：

构建的最小堆：
[18, 20, 44, 29, 30, 93, 71, 75, 56, 65]
调整后数组：
[68, 75, 71, 75, 75, 93, 84, 675, 234, 676]

大根堆的实现和排序与小根堆同理，大同小异。

堆排序的复杂度

初始化建堆的时间复杂度为O(n)，排序重建堆的时间复杂度为nlog(n)，所以总的时间复杂度为O(n+nlogn)=O(nlogn) ，因为堆排序是就地排序，所以空间复杂度为O（1）