多校训练第1轮.A——À la Volonté du Peuple【最短路】

题目传送门

---

题目背景

Please note that we changed the sample input 1 a little bit to fit the illustration. The answer for either version is correct though. PDF updated. Sorry for troubles caused.

---

题目描述

Will you give all you can give
So that our banner may advance?
Some will fall and some will live
Will you stand up and take your chance?
The blood of the martyrs
Will water the meadows of France!

A solitary spark can start a prairie fire.

You are given a weighted connected undirected graph with nn vertices and mm edges. You know that someone light up a fire at vertex 11, which will burn the current position into dust immediately and expand to adjacent places at the speed 11 mile per second. The fire will split at the vertices to all those edges who have not been lighten up, and will cause a blast when at least two fires meet at the same point.

Revolutionaries love explosions. They want you to count the number of explosions that will happen on the graph.

---

输入格式

The first line contains integers $n,m(1\le n\le 3\times 10^5,0\le m\le 10^6)$ - the number of vertices.

Each of the next mm lines contains $3$ integers $u_i,v_i,w_i(1\le u_i,v_i\le n,1\le w_i\le 9)$ - the ends of the $i\text{-th}$ edge and the weight of the $i\text{-th}$ edge.

It’s guaranteed that the graph is connected.

The graph may contain self loops and multiple edges. Example 11 shows the method to deal with them.

The size of input file may be large. Please, do not read input by too slow ways.

---

输出格式

Output the number of explosions that will happen on the graph in a single line.

输入

2 3
1 1 1
1 2 1
1 2 1

4 5
1 2 1
1 3 1
2 3 1
2 4 1
3 4 1

---

输出

2

2

---

说明/提示

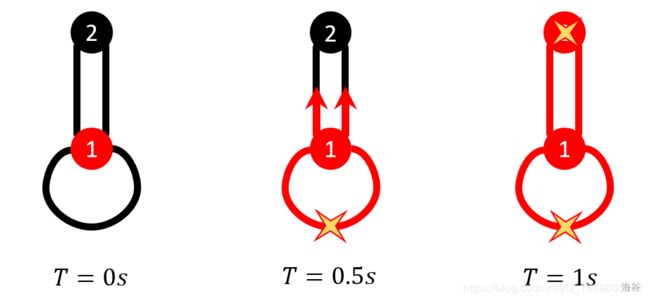
Here’s the illustration for example 1:

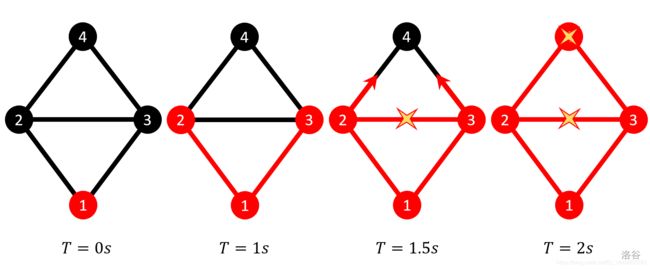
Here’s the illustration for example 2:

---

题意

• 给你一个 $n$ 个点的无向图（允许自环）
• 从编号为 $1$ 的点开始点火，然后沿着边跑，可以分身（说白了就是火药被点着了）
• 当火药被两个以上不同方向同时被点燃的时候，会发生爆炸
• 询问能发生几次爆炸
• $1\le n\le 3\times 10^5,0\le m\le 10^6,1\le w_i\le 9$

---

题解

• 火药燃烧的过程其实就是在跑 最短路
• 在点上爆炸意味着存在至少两个点可以是他最短路上的前驱；
• 在边上爆炸意味着**这条边不在最短路里。
• 因此求出最短路即可。
• 边权 ≤ 9 并不意味着可以使用 SPFA。
• 本题的本意是使用 $O(nw)$ 的桶排序 $Dijkstra,$ 但是由于 $vector$ 实现的桶排 $Dijkstra$ 和邻接表 + $priorit{y}_{q}ueue$ 实现的 $O(mlogm)$ $Dijkstra$ 速度在使用输入随机数生成器的方法开大数据后没法拉开差距，因此为了避免卡常数都放了过去。
• 本题真的不卡常数，测出来时限不宽是因为读入太慢了。

---

AC-Code $开O2优化$

#include 
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;

const int maxn = 3e5 + 7;
const int maxm = 1e6 + 7;
struct P {
	int to, val;
	P() { to = val = 0; }
	P(int a, int b) :to(a), val(b) {};
	bool operator < (const P& t)const { return val > t.val; }
};
vector<P> G[maxm];
int dis[maxn];
bool vis[maxn];
void add(int u, int v, int w) {
	G[u].push_back(P(v, w));
	if (u != v)	G[v].push_back(P(u, w));
}
void dijk() {
	memset(dis, 0x3f, sizeof dis);
	memset(vis, false, sizeof vis);
	priority_queue<P> q;
	q.push(P(1, 0));	dis[1] = 0;
	while (!q.empty()) {
		P tmp = q.top();	q.pop();
		if (vis[tmp.to])	continue;
		vis[tmp.to] = true;
		for (int i = 0; i < G[tmp.to].size(); ++i) {
			int pos = G[tmp.to][i].to;
			int value = G[tmp.to][i].val;
			if (dis[pos] > dis[tmp.to] + value) {
				dis[pos] = dis[tmp.to] + value;
				q.push(P(pos, dis[pos]));
			}
		}
	}
}
int main() {
	ios;
	int n, m;	while (cin >> n >> m) {
		for (int i = 1; i <= m; ++i) {
			int u, v, w;	cin >> u >> v >> w;
			add(u, v, w); // 无向图
		}
		dijk(); // 跑一边最短路
		int ans = 0;
		for (int i = 1; i <= n; ++i) {
			int cnt = 0;
			for (P v : G[i]) { // v:点i的邻接点+权值，前驱、后继。
				if (dis[i] == dis[v.to] + v.val) // 找交点爆炸
					++cnt; // v->i和dis[i]相同，v可以是最短路上的点
				else if (i >= v.to && dis[i] + v.val > dis[v.to] && dis[v.to] + v.val > dis[i])	   ++ans;
			}
			if (cnt > 1)	++ans; // 俩以上前驱等距离，在交点爆炸1次
		}
		cout << ans << endl;
	}
}