RNN-LSTM-GRU

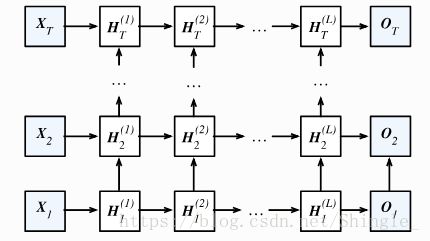
循环神经网络（Recurrent Neural Network, RNN）

假设 Xt∈Rn×d X t ∈ R n × d 是序列中时间步 t 的小批量输入 Ht∈Rn×h H t ∈ R n × h 该时间步的隐藏层变量。跟多层感知机不同在于这里我们保存上一时间步的隐藏变量 Ht−1 H t − 1 并引入一个新的权重参数 Whh∈Rh×h W h h ∈ R h × h ，它用来描述在当前时间步如何使用上一时间步的隐藏变量。具体来说，当前隐藏变量的计算由当前输入和上一时间步的隐藏状态共同决定：

Ht=ϕ(XtWxh+Ht−1Whh+bh), H t = ϕ ( X t W x h + H t − 1 W h h + b h ) ,

这里隐藏变量捕捉了截至当前时间步的序列历史信息，就像是神经网络当前时间步的状态或记忆一样，因此也称之为隐藏状态。

Ot=HtWhy+by. O t = H t W h y + b y .

def rnn(inputs, state, params):
    # inputs 和 outputs 皆为 num_steps 个形状为（batch_size, vocab_size）的矩阵。
    W_xh, W_hh, b_h, W_hy, b_y = params
    H, = state
    outputs = []
    for X in inputs:
        H = nd.tanh(nd.dot(X, W_xh) + nd.dot(H, W_hh) + b_h)
        Y = nd.dot(H, W_hy) + b_y
        outputs.append(Y)
    return outputs, (H,)

深度循环神经网络

H(1)t=ϕ(XtW(1)xh+H(1)t−1W(1)hh+b(1)h), H t ( 1 ) = ϕ ( X t W x h ( 1 ) + H t − 1 ( 1 ) W h h ( 1 ) + b h ( 1 ) ) ,

H(l)t=ϕ(H(l−1)tW(l)xh+H(1)t−1W(l)hh+b(l)h), H t ( l ) = ϕ ( H t ( l − 1 ) W x h ( l ) + H t − 1 ( 1 ) W h h ( l ) + b h ( l ) ) ,

Ot=H(L)tWhy+by, O t = H t ( L ) W h y + b y ,

双向循环神经网络

H→t=ϕ(XtW(f)xh+H→t−1W(f)hh+b(f)h) H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) )

H←t=ϕ(XtW(b)xh+H←t+1W(b)hh+b(b)h), H ← t = ϕ ( X t W x h ( b ) + H ← t + 1 W h h ( b ) + b h ( b ) ) ,

Ht=concat(H→t,H←t)Ht∈Rn×2h H t = c o n c a t ( H → t , H ← t ) H t ∈ R n × 2 h

Ot=HtWhy+by, O t = H t W h y + b y ,

梯度裁剪

循环神经网络中较容易出现梯度衰减或爆炸，为了应对梯度爆炸，我们可以裁剪梯度（clipping gradient）。假设我们把所有模型参数梯度的元素拼接成一个向量 g，并设裁剪的阈值是 θ。裁剪后梯度的 L2 范数不超过 θ。：

min(θ∥g∥,1)g min ( θ ‖ g ‖ , 1 ) g

def grad_clipping(params, theta, ctx):
    norm = nd.array([0.0], ctx)
    for param in params:
        norm += (param.grad ** 2).sum()
    norm = norm.sqrt().asscalar()
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm

http://zh.gluon.ai/chapter_recurrent-neural-networks/rnn-scratch.html

梯度裁剪可以解决梯度爆炸的问题，梯度衰减呢？ -> 门控单元

---

LSTM

输入门、遗忘门和输出门:

It=σ(XtWxi+Ht−1Whi+bi) I t = σ ( X t W x i + H t − 1 W h i + b i )

Ft=σ(XtWxf+Ht−1Whf+bf) F t = σ ( X t W x f + H t − 1 W h f + b f )

Ot=σ(XtWxo+Ht−1Who+bo), O t = σ ( X t W x o + H t − 1 W h o + b o ) ,

候选记忆细胞:

C~t=tanh(XtWxc+Ht−1Whc+bc), C ~ t = tanh ( X t W x c + H t − 1 W h c + b c ) ,

记忆细胞:

Ct=Ft⊙Ct−1+It⊙C~t. C t = F t ⊙ C t − 1 + I t ⊙ C ~ t .

隐藏状态:

Ht=Ot⊙tanh(Ct). H t = O t ⊙ tanh ( C t ) .

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hy, b_y] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = nd.sigmoid(nd.dot(X, W_xi) + nd.dot(H, W_hi) + b_i)
        F = nd.sigmoid(nd.dot(X, W_xf) + nd.dot(H, W_hf) + b_f)
        O = nd.sigmoid(nd.dot(X, W_xo) + nd.dot(H, W_ho) + b_o)
        C_tilda = nd.tanh(nd.dot(X, W_xc) + nd.dot(H, W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * C.tanh()
        Y = nd.dot(H, W_hy) + b_y
        outputs.append(Y)
    return outputs, (H, C)

GRU

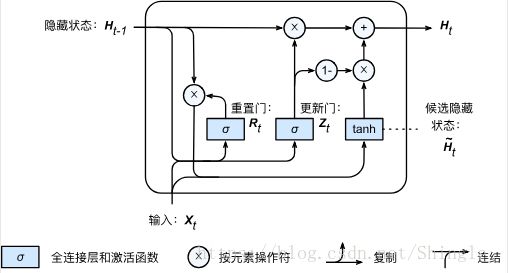
重置门和更新门:

Rt=σ(XtWxr+Ht−1Whr+br) R t = σ ( X t W x r + H t − 1 W h r + b r )

Zt=σ(XtWxz+Ht−1Whz+bz) Z t = σ ( X t W x z + H t − 1 W h z + b z )

候选隐藏状态:

H~t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh), H ~ t = tanh ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h ) ,

隐藏状态:

Ht=Zt⊙Ht−1+(1−Zt)⊙H~t. H t = Z t ⊙ H t − 1 + ( 1 − Z t ) ⊙ H ~ t .

def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hy, b_y = params
    H, = state
    outputs = []
    for X in inputs:
        Z = nd.sigmoid(nd.dot(X, W_xz) + nd.dot(H, W_hz) + b_z)
        R = nd.sigmoid(nd.dot(X, W_xr) + nd.dot(H, W_hr) + b_r)
        H_tilda = nd.tanh(nd.dot(X, W_xh) + R * nd.dot(H, W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = nd.dot(H, W_hy) + b_y
        outputs.append(Y)
    return outputs, (H,)

---

http://www.tensorfly.cn/tfdoc/tutorials/recurrent.html

Recurrent Neural Network Regularization - Wojciech Zaremba, Ilya Sutskever, Oriol Vinyals https://arxiv.org/abs/1409.2329

https://github.com/tensorflow/models/tree/master/tutorials/rnn

Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.

Cho, K., Van Merri ë nboer, B., Bahdanau, D., & Bengio, Y. (2014). On the properties of neural machine translation: Encoder-decoder approaches. arXiv preprint arXiv:1409.1259.

Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555.

http://karpathy.github.io/2015/05/21/rnn-effectiveness/

http://deeplearning.net/tutorial/lstm.html#lstm

http://colah.github.io/posts/2015-08-Understanding-LSTMs/

https://distill.pub/2016/augmented-rnns/