Leetcode 第192场周赛题解

5428. 重新排列数组

• 时间复杂度：O(n)
• 知识点：构造

根据规则计算每个元素的新位置，然后创建一个新的 vector 用来存储移动后的元素。

class Solution {
public:
    vector<int> shuffle(vector<int>& nums, int n) {
        n *= 2;
        vector<int> anw; anw.resize(n);
        for(int i = 0; i < n; i++) {
            if(i < n/2) {
                anw[i*2] = nums[i];
            } else {
                anw[(i-n/2)*2 + 1] = nums[i];
            }
        }
        return anw;
    }
};

5429. 数组中的 k 个最强值

• 知识点：排序
• 时间复杂度：O(n*logn)

先对 arr 进行一趟升序排序，以获得中位数。
根据题目中的强弱规则实现 compare 函数对象，再进行一次排序。
最后取前 k 个即可。

class Solution {
public:
    vector<int> getStrongest(vector<int>& arr, int k) {
        sort(arr.begin(), arr.end());
        int mid = arr[(arr.size()-1)/2];
        sort(arr.begin(), arr.end(), [mid](int a, int b) -> bool {
            if(abs(a-mid) == abs(b-mid)) {
                return a > b;
            }
            return abs(a-mid) > abs(b-mid);
        });
        return vector<int>(arr.begin(), arr.begin()+k);
    }
};

5430. 设计浏览器历史记录

• 知识点：栈
• 时间复杂度：O(n)，n 为操作次数

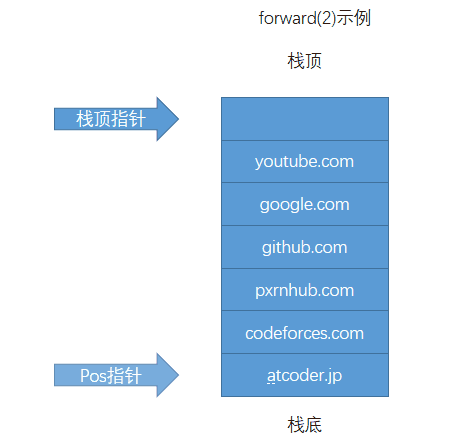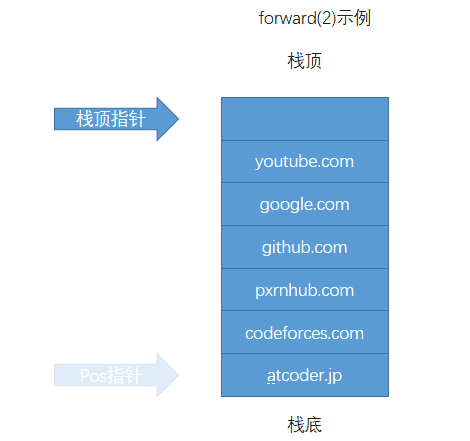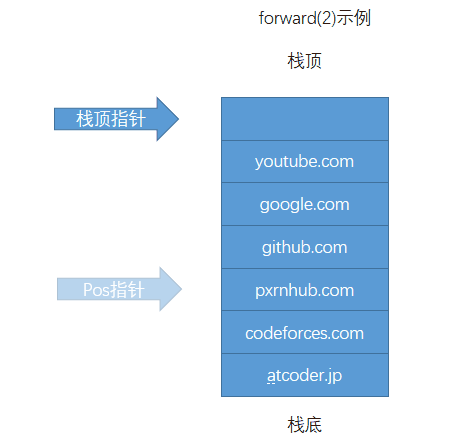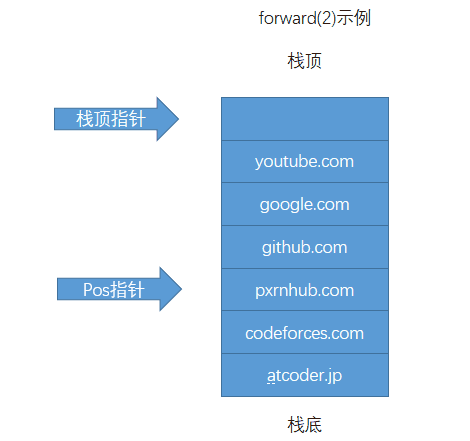
使用一个栈记录浏览历史，使用一个 pos 记录当前网页在栈中的位置。每次 back 和 forward 操作都只更新 pos 。因为visit操作会把浏览历史前进的记录全部删除，所以每次 visit 先根据 pos 更新下栈顶指针，然后再将 url 入栈。
可以先看图在看代码~

class BrowserHistory {
public:
    int pos;
    int top;
    string history[5001];
    BrowserHistory(string homepage) : pos(-1), top(0) {
        visit(homepage);
    }
    
    void visit(string url) {
        pos ++;
        top = pos;
        history[top++] = url;
    }
    
    string back(int steps) {
        if(steps > pos) {
            steps = pos;
        }
        pos -= steps;
        return history[pos];
    }
    
    string forward(int steps) {
        steps = min(steps, top - pos - 1);
        pos += steps;
        return history[pos];
    }
};

5431. 给房子涂色 III

• 知识点：动态规划
• 时间复杂度：O(m*target*n*n)

f(i,j,k) 表示将前 i 个房子 分成 j 段，且第i个房子的颜色为 k 时的最小花费。
如果房子颜色不是固定的，需要枚举所有颜色。
状态转移方程为：
f(i,j,k) = min(f(i-1, j, k) + cost(i, k), f(i-1, j-1, p) + cost(i,p) ) (p != k)。

class Solution {
public:
    int getCost(int color, int newColor, int cost) {
        if(color == newColor) {
            return 0;
        }
        return cost;
    }
    int minCost(vector& houses, vector>& cost, int m, int n, int target) {
        uint64_t dp[101][101][20];
        memset(dp, 0x0777, sizeof(dp));
        for(int i = 0; i < n; i++) {
            dp[0][0][i] = 0;
        }
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= i && j <= target; j++) {
                if(houses[i-1] == 0) {
                    for(int k = 0; k < n; k++) {
                        dp[i][j][k] = min(dp[i][j][k], dp[i-1][j][k] + getCost(k, houses[i-1]-1, cost[i-1][k]));

                        for(int c = 0; c < n; c++) {
                            if(c == k ) { continue; }
                            dp[i][j][k] = min(dp[i][j][k], dp[i-1][j-1][c] + getCost(k, houses[i-1]-1, cost[i-1][k]));
                        }
                    }
                } else {
                    int c = houses[i-1] - 1;
                    dp[i][j][c] = min(dp[i][j][c], dp[i-1][j][c]);
                    for(int p = 0; p < n; p++) {
                        if(p == c) { continue; }
                        dp[i][j][c] = min(dp[i][j][c], dp[i-1][j-1][p]);
                    }
                }
            }
        }
        uint64_t anw = dp[m][target][0];
        for(int i = 0; i < n; i++) {
            anw = min(anw, dp[m][target][i]);
        }
        if(anw > 100 * 10000) {
            return -1;
        }
        return anw;
    }
};