排列问题的重参数技巧
近日研读了一篇发表在ICLR 2018上的文章:《LEARNING LATENT PERMUTATIONS WITH GUMBEL- SINKHORN NETWORKS》, 其介绍了一种能够将二维张量以可微分的形式转变为转置矩阵的方法。使得指派、重排等不可微分操作能够以可微分的形式结合到神经网络当中。由此,我们便可使BP算法学习这些操作,以实现神经网络的数字排序、拼图等算法。
BP之痛
直面评价指标?
其实我在最初使用神经网络分类时有一个很幼稚的想法,对于最后的分类。能否设计这样一个损失函数:
l o s s _ s i n g l e = { 0 p r e d i c t = = y 1 p r e d i c t ! = y loss\_single = \begin{cases} 0 & predict == y \\ 1 & predict \ != y \end{cases} loss_single={01predict==ypredict !=y
最后,我们取所有样本损失的平均为最终的loss。这样我们就可以直接优化最终的指标:准确率,不是很美好吗?实现见以下代码:
import torch
x = torch.randn(5, requires_grad=True)
_, predict = torch.max(x, 0)
y = torch.LongTensor([1])
loss = (predict != y).int()
print("x:{}\nidx:{}\nloss:{}\n".format(x, idx, loss))
> x:tensor([-0.7181, -0.2303, -1.4065, 2.0853, -0.9006], requires_grad=True)
> idx:3
> loss:tensor([1], dtype=torch.int32)
不可导!
上面的逻辑粗略来看是没问题的,但是,有一个很重要的漏洞。我们调用了torch.max函数,返回了预测结果predict,然后去和 y y y比较计算损失。
但是很遗憾:选取最高概率类别这个操作,即函数 a r g m a x i ( x ) argmax_i(x) argmaxi(x)是不可导的。我们没有办法记录这一个操作的梯度。也就无法使用BP算法更新网络(可以看到上方输出中loss并没有记录到梯度信息).
近似之法
既然上述方法失败在:$argmax$这个函数不可导上,那我们能不能进行解决呢,答案自然是可以的。简单来说,我们可以通过以下可导函数近似argmax函数(准确来说,是近似onehot(argmax)函数:
s o f t m a x ( x τ ) , τ → 0 softmax(\frac{x}{\tau}), \tau \to 0 softmax(τx),τ→0
如果需要具体解释,参考《函数光滑化杂谈:不可导函数的可导逼近》。
排列问题
如果我们希望求得一个最优排列,常见的,比如使用匈牙利算法解决最优指派问题,同样,这个选取最优指派的操作是不可导的,那么,我们也就不能使用神经网络去学习这个问题。因此,类比分类问题:我们能不能也使用一个可导的操作去近似选取最优指派这个操作呢,从而使得可以被学习呢?答案是可以的
Sinkhorn operator
我们知道,一个指派,实际上可以等价为一个置换矩阵 P P P,如下所示:
[ 0 1 0 1 0 0 0 0 1 ] ⏟ P [ 1 2 3 ] ⏟ x = [ 2 1 3 ] ⏟ x \underbrace{ \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} }_{P} \underbrace{ \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} }_x =\underbrace{ \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} }_x P ⎣⎡010100001⎦⎤x ⎣⎡123⎦⎤=x ⎣⎡213⎦⎤
所以,我们能否可微地去近似置换矩阵 P P P呢,从而通过学习 P P P去学习指派这个操作呢?答案是可以,方法就是Sinkhorn operator。
给定一个方阵 X X X. 我们可以通过以下变幻将其变为双线性矩阵。(所谓双线性矩阵,就是其每一行每一列的和都为1).
S 0 ( X ) = exp ( X ) S l ( X ) = T c ( T r ( S l − 1 ( X ) ) ) S ( X ) = lim l → ∞ S l ( X ) \begin{aligned} S^{0}(X) &=\exp (X) \\ S^{l}(X) &=\mathcal{T}_{c}\left(\mathcal{T}_{r}\left(S^{l-1}(X)\right)\right) \\ S(X) &=\lim _{l \rightarrow \infty} S^{l}(X) \end{aligned} S0(X)Sl(X)S(X)=exp(X)=Tc(Tr(Sl−1(X)))=l→∞limSl(X)
当然,对于指派问题,仅仅是双线性矩阵还是不够的,因为我们要保证$S(x)$中的元素是非0即1的。而这个限制,我们可以通过增加一个超参数$\tau$实现:
M ( X ) = lim τ → 0 + S ( X / τ ) M(X)=\lim _{\tau \rightarrow 0^{+}} S(X / \tau) M(X)=τ→0+limS(X/τ)
其中, M ( X ) = arg max P ∈ P N ⟨ P , X ⟩ F M(X)=\underset{P \in \mathcal{P}_{N}}{\arg \max }\langle P, X\rangle_{F} M(X)=P∈PNargmax⟨P,X⟩F为对应收益矩阵为 X X X的最优置换矩阵, ⟨ A , B ⟩ F = trace ( A ⊤ B ) \langle A, B\rangle_{F}=\operatorname{trace}\left(A^{\top} B\right) ⟨A,B⟩F=trace(A⊤B)`
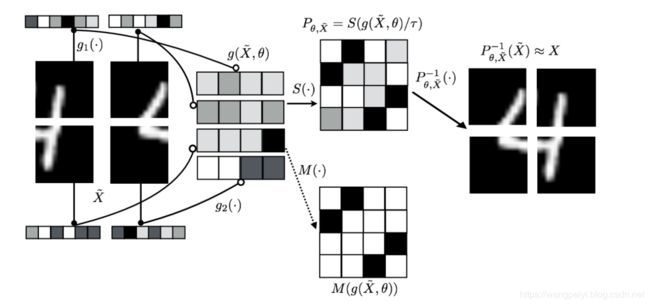
这样,我们通过神经网络去将原始数据编码为矩阵 X X X, 再通过可微操作 lim τ → 0 + S ( X / τ ) \lim _{\tau \rightarrow 0^{+}} S(X / \tau) limτ→0+S(X/τ)近似 X X X对应的指派 M ( X ) M(X) M(X)。最后就可以实现梯度更新从而训练网络了。
实验
个人使用Pytorch复现了一遍原文给出的数字排序实验: