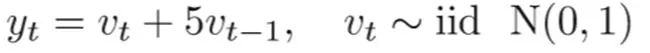【机器学习基础】时间序列测试题的40题,看看你对时间序列的了解水平
磐创AI分享
作者 | SAURABH JAJU
编译 | Flin
来源 | analyticsvidhya
介绍
时间序列预测与建模在数据分析中起着重要的作用。时间序列分析是统计学的一个分支,广泛应用于计量经济学和运筹学等领域。这篇技能测试文章是为了测试你对时间序列概念的了解程度。
共有1094人报名参加了这次技能测试。这个测试是为了测试你对时间序列的了解的水平。如果你错过了这次技能测试,这里有一些问题和对应的解决方案。如果你错过了实时测试,也可以通过阅读本文以了解你有多少题目是可以正确回答的。
这是所有参赛者的排行榜
https://datahack.analyticsvidhya.com/contest/avdatafest-skillpower-time-series/#LeaderBoard
所有的得分
下面是分布得分,它们将帮助你评估你的表现。
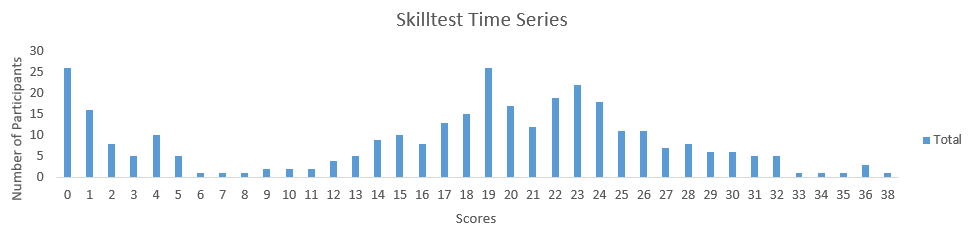
你可以在下方链接查看分数。
https://datahack.analyticsvidhya.com/contest/avdatafest-skillpower-time-series/#LeaderBoard
300多人参加了技能测试,获得的最高分数为38分。以下是一些关于分布的统计数据。
平均分:17.13
中位数:19
众数:19
1) 下面哪一个是时间序列问题的例子?
估计未来6个月酒店客房预订数量。
估计保险公司未来三年的总销售额。
估计下一周的通话次数。
A) 只有 3 B) 1 和 2 C) 2 和 3 D) 1 和 3 E) 1,2 和 3
解决方案:(E)
以上所有选项都与时间序列有关。
2) 以下哪项不是时间序列模型的示例?
A) 朴素法
B) 指数平滑
C) 移动平均
D) 以上都不是
解决方案:(D)
朴素法:一种估计技术,在这种技术中,最后一个时期的实际情况被用作这一时期的预测,而不加以调整或试图确定因果因素,适用于比较稳定的序列。它仅用于与更复杂的技术生成的预测进行比较。
在指数平滑中,旧数据的相对重要性逐渐降低,而新数据的相对重要性逐渐提高。
在时间序列分析中,移动平均(MA)模型是一种常用的单变量时间序列建模方法。移动平均模型指定输出变量线性依赖于随机项(不完全可预测)的当前值和各种过去值。
3) 下列哪项不能作为时间序列图的组成部分?
A) 季节性
B) 趋势
C) 周期性
D) 噪声
E) 以上都不是
解决方案:(E)
当一系列因素受到季节因素(例如,一年中的一个季度、一个月或一周中的一天)的影响时,就存在一种季节模式。季节性总是一个固定且已知的时期。因此,季节性时间序列有时被称为周期性时间序列
季节总是一个固定且已知的时期。当数据呈现非固定周期的涨跌时,它就存在一种循环模式。
趋势被定义为时间序列中跟日历无关且无规律影响的“长期”运动,是底层的反映。它是人口增长、物价上涨和一般经济变化等影响的结果。下图描绘了一个随时间有明显上升趋势的系列。

噪声:在离散时间内,白噪声是一种离散信号,其样本被视为一系列均值为零、方差有限的不相关随机变量。
因此,上述所有内容都是时间序列的组成部分。
4) 在时间序列建模中,下列哪项比较容易估计?
A) 季节性
B) 周期性
C) 季节性和周期性没有区别
解决方案:(A)
正如我们在前面的解中所看到的,由于季节性呈现平稳的结构,所以更容易估计。
5) 下面的时间序列图包含周期性和季节性成分

A)真 B)假
解决方案: (B)
上面的图中以固定的时间间隔重复出现差不多的趋势,因此实际上只是季节性的。
6)时间序列数据(不包括白噪声)中的相邻观测值是独立且均匀分布的(IID)
A)真 B)假
解决方案:(B)
随着观测值之间的时间间隔变短,它们往往与时间强相关。因为时间序列预测是基于以前的观察数据而不是当前的观察数据,不像分类或回归那样数据与数据之间关联性不高。
7) 接近1的平滑参数会给预测中的最新观测值带来更大的权重或影响
A) 真
B) 假
解决方案:(A)
将较大的权重应用于较新的观测结果中,比应用到历史数据的观测结果中更为明智。这正是简单指数平滑背后的概念。预测是使用加权平均值计算的,加权平均值随着过去观测值的增加呈指数递减——最小的权重将与最早的观测值相关。
8)指数平滑的权重之和是_____
A)<1 B)1 C)> 1 D)以上都不是
解决方案: (B)
表7.1显示了使用简单指数平滑法进行预测时,对四个不同α值的观测值的权重。请注意,对于任何合理的样本量,即使对于较小的α,权重的总和也将约为1。
| Observation | α=0.2 | α=0.4 | α=0.6 | α=0.8 |
| yT | 0.2 | 0.4 | 0.6 | 0.8 |
| yT−1 | 0.16 | 0.24 | 0.24 | 0.16 |
| yT−2 | 0.128 | 0.144 | 0.096 | 0.032 |
| yT−3 | 0.102 | 0.0864 | 0.0384 | 0.0064 |
| yT−4 | (0.2)(0.8) | (0.4)(0.6) | (0.6)(0.4) | (0.8)(0.2) |
| yT−5 | (0.2)(0.8) | (0.4)(0.6) | (0.6)(0.4) | (0.8)(0.2) |
9)上一阶段的预测是70,而需求是60。什么是简单的指数平滑?当Alpha = 0.4时,预测下一个周期。
A) 63.8 B) 65 C) 62 D) 66
解决方案:(D) Yt-1 = 70 St-1 = 60 Alpha = 0.4
代入,得:
0.4 * 60 + 0.6 * 70 = 24 + 42 = 66
10)自协方差测量什么?
A) 不同时间观测到的不同序列上多个点之间的线性相关性
B) 不同时间观测到的同一序列上两点之间的二次相关性
C) 同时观测到的不同序列两点之间的线性关系
D) 在不同时间观测到的同一序列上两点之间的线性关系
解决方案:(D)
选项D是自协方差的定义。
11) 下列哪项不是弱平稳时间序列的必要条件?
A) 平均值是恒定的,不依赖于时间
B) 自协方差函数仅通过其差|s-t|依赖于s和t(其中t和s为时刻)
C) 所考虑的时间序列是一个有限方差过程
D) 时间序列是高斯的
解决方案:(D)
高斯时间序列意味着平稳性是严平稳性。
12) 下列哪项不是平滑时间序列的技术?
A) 最近邻回归
B) 局部加权散点图平滑
C) 基于树的模型,如(CART)
D) 平滑样条曲线
解决方案:(C)
时间序列平滑和滤波可以用局部回归模型来表示。多项式和回归样条也提供了平滑的重要技术。基于CART的模型不提供要叠加在时间序列上的方程,因此不能用于平滑。所有其他技术都是有据可查的平滑技术。
13)如果2016年10月需求为100,2016年11月需求为200,2016年12月需求为300,2017年1月需求为400。2017年2月的3个月移动平均线是多少?
A)300
B) 350
C) 400
D)需要更多的信息
解决方案:(A)
X' = (xt-3 + xt-2 + xt-1) /3
(200+300+400)/ 3 = 900/3 =300
14)查看下面的ACF图,你是否建议将AR或MA用于ARIMA建模技术?
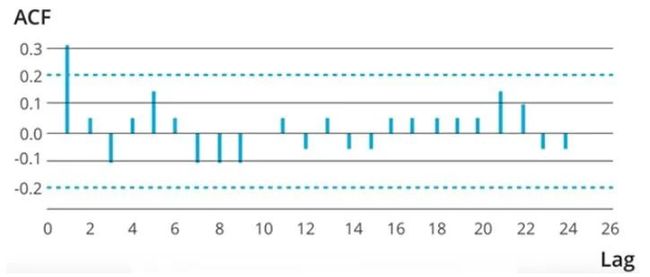
A)AR B)MA C)不能判断
解决方案:(A)
在以下情况下考虑使用MA模型:如果差分序列的自相关函数(ACF)表现出明显的截尾或偏相关系数表现出拖尾,则考虑添加一个模型的MA项。ACF截止的滞后时间就是MA项数。
但是,由于没有表现出明显的截尾,因此必须采用AR模型。
15)假设你是Analytics Vidhya的一名数据科学家。你注意到1 - 3月对文章的评论增加了。而11月- 12月期间的浏览量有所下降。
以上陈述是否代表数据具有季节性?
A)真 B)假 C)不能判断
解决方案:(A)
是的,这是一个明确的季节性趋势,因为在特定时间视图会发生变化。
请记住,“季节性”是指在特定的周期性时间间隔内出现的变化。
16)以下哪个图形可用于检测时间序列数据中的季节性?
1.多个盒图 2.自相关
A)仅1 B)仅2 C)1和2 D)这些都不是
解决方案:(C)
季节性是在特定的周期间隔内变化的存在。
分布的变化可以在多个盒图中观察到。因此,可以很容易地发现季节性。自相关图应在等于周期的滞后处显示峰值。
17)平稳性是时间序列过程的理想属性。
A)是 B)假
解决方案:(A)
当满足以下条件时,时间序列是平稳的。
平均值是恒定的,不依赖于时间
自协方差函数仅取决于s和t的差| s-t |。(其中t和s是时间点)
考虑的时间序列是一个有限方差过程
这些条件是数学上表示要用于分析和预测的时间序列的必要先决条件。因此,平稳性是理想的属性。
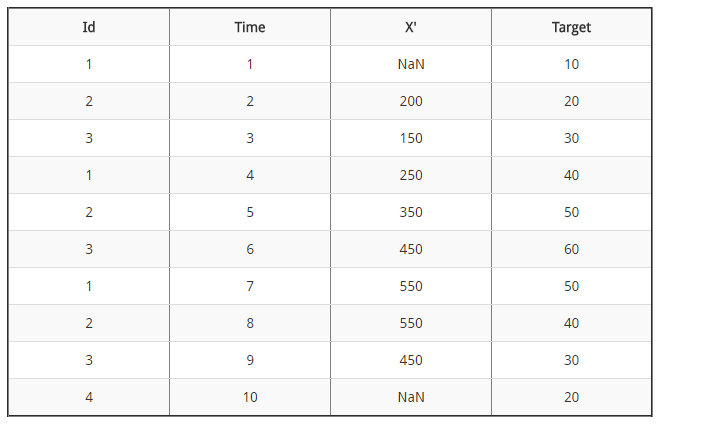
18)假设你获得的时间序列数据集只有4列(id,Time,X,Target)

如果给定窗口大小2,特征X的滑动平均值是多少?
注意:X栏代表滑动平均值。
D)以上都不是
解决方案: (B)
X` = Xt-2 + Xt-1 / 2
根据以上公式:(100 +200)/ 2 = 150; (200 + 300)/ 2 = 250,依此类推。
19)想象一下,你正在处理时间序列数据集。你的经理要求你建立一个高度准确的模型。你开始构建以下两种类型的模型。
模型1:决策树模型
模型2:时间序列回归模型
在对这两个模型进行评估的最后,你发现模型2比模型1更好。
A)模型1不能像模型2那样映射线性关系 B)模型1总是比模型2更好 C)你不能将决策树与时间序列回归进行比较 D)这些都不是
解决方案: (A)
时间序列模型类似于回归模型。因此,它擅于找到简单的线性关系。基于树的模型虽然有效,但在发现和利用线性关系方面却并不那么擅长。
20)哪种类型的分析对于根据以下类型的数据进行温度预测最有效。
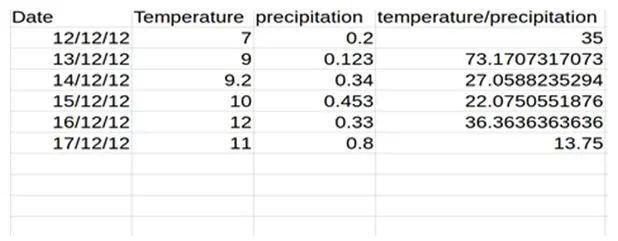
A)时间序列分析 B)分类 C)聚类 D)以上都不是
解决方案:(A)
本题获取了连续几天的数据,因此最有效的分析类型是时间序列分析。
21)温度/降水变量的一次差分是多少?

A)15,12.2,-43.2,-23.2,14.3,-7 B)38.17,-46.11,-4.98,14.29,-22.61 C)35,38.17,-46.11,-4.98,14.29,-22.61 D)36.21, -43.23,-5.43,17.44,-22.61
解决方案:(B)
73.17-35 = 38.17 27.05-73.17 = – 46.11,依此类推。13.75 – 36.36 = -22.61
22)考虑以下数据集:
「{23.32 32.33 32.88 28.98 33.16 26.33 29.88 32.69 18.98 21.23 26.66 29.89} 时间序列滞后一个样本的自相关是什么?」
A) 0.26 B) 0.52 C) 0.13 D) 0.07
解决方案:(C)
ρˆ1 = PT t = 2(x t-1- x¯)(x t- x¯)PTt = 1(xt-x¯)^2
=(23.32-x′)(32.33-x′)+(32.33-x′)(32.88-x′)+···PT t = 1(xt -x′)^2
= 0.130394786
其中x是级数的平均值,为28.0275
23)任何平稳时间序列都可以近似为在各种频率下振荡的正弦和余弦的随机叠加。
A)真 B)假
解决方案:(A)
弱平稳时间序列 xt 是有限方差过程,因此
平均值函数 µt 是常数,并且不依赖于时间t;并且(ii)定义的自协方差函数γ(s,t)仅依赖于s和t的差| s-t |。
在各种频率下振荡的正弦和余弦的随机叠加是白噪声。白噪声是微弱的或平稳的。如果白噪声变量也呈正态分布或高斯分布,则该序列也是严平稳的。
24)弱平稳时间序列的自协方差函数不取决于_______?
A)xs和xt的间隔 B)h = | s – t | C)在特定时间点的位置
解决方案:(C)
通过定义上一个问题中描述的弱平稳时间序列。
25)如果_____,则两个时间序列联合平稳。
A)它们都是平稳的 B)交叉方差函数仅是滞后h的函数 C)仅A D)A和B
解决方案:(D)
联合平稳性是根据上述两个条件定义的。
26)在自回归模型中_______
A)因变量的当前值受自变量的当前值影响 B)因变量的当前值受自变量的当前值和过去值影响 C)因变量的当前值受因变量和自变量的过去值影响 D)以上都不是
解决方案:(C)
自回归模型基于这样的思想,即序列的当前值xt可以解释为p个过去值xt-1,xt-2,…,xt-p的函数,其中p决定了预测当前值所需的过去步进数。例如 xt = xt-1 -.90xt-2 + wt,
其中xt-1和xt-2是因变量和wt的过去值,白噪声可以表示独立值。
该示例可以扩展为包括类似于多元线性回归的多序列。
27)对于MA(移动平均值)模型,对 σ=1 和 θ=5 产生与对 σ=25 和θ=1/5 相同的自协方差函数。
A)真 B)假
解决方案:(A)
正确,因为MA模型的自协方差是可逆的
请注意,对于MA(1)模型,对于θ和1 /θ,ρ(h)相同。
28)通过查看下面的ACF和PACF图,可以在时间序列中包括多少个AR和MA项?

A)AR(1)MA(0) B)AR(0)MA(1) C)AR(2)MA(1) D)AR(1)MA(2) E)不能判断
解决方案:(B)
滞后1的强负相关表明MA只有1个显著滞后。阅读本文以获得更好的理解。
https://www.analyticsvidhya.com/blog/2015/12/complete-tutorial-time-series-modeling/
29)对于白噪声,以下哪项是正确的?
A)均值= 0 B)自协方差为0 C)自协方差为0(零滞后除外 D)二次方差
解决方案:(C)
白噪声过程必须具有恒定的均值,恒定的方差和无自协方差结构(滞后零(方差)除外)。
30)对于以下MA(3)过程 yt = μ + Εt + θ1Εt-1 + θ2Εt-2 + θ3Εt-3 ,其中σt是方差为σ2的零均值白噪声过程。
A)在滞后3时ACF = 0 B)在滞后5中ACF = 0 C)在滞后1中ACF = 1 D)在滞后2中ACF = 0 E)在滞后3和滞后5中ACF = 0
解决方案:(B)
回想一下,MA(q)过程仅具有长度为q的记忆。这意味着,所有自相关系数在滞后q以后的值为零。这可以通过检查MA方程并看到只有过去的q个扰动项进入方程来看出。
因此,如果我们向前迭代此方程超过q个周期,则扰动项的当前值将不再影响y。由于滞后零的自相关函数是时间t处的y与时间t处的y的相关性(即y_t与自身的相关性),因此根据定义,滞后0处的自相关函数必须为1。
31)考虑下面的AR(1)模型,其扰动项具有零均值和单位方差。yt = 0.4 + 0.2 yt-1 + ut, y的(无条件)方差由____给出。
A)1.5 B)1.04 C)0.5 D)2
解决方案:(B)
扰动的方差除以(1减去自回归系数的平方)
在这种情况下为:1 /(1-(0.2 ^ 2))= 1 / 0.96 = 1.041
32)pacf(部分自相关函数)对于区分______是必需的。
A)AR和MA模型:错误 B)AR和ARMA模型:正确 C)MA和ARMA模型:错误 D)ARMA系列中的不同模型
解决方案:(B)

33)时间序列的二次差分可以帮助消除哪个趋势?
A)二次趋势 B)线性趋势 C)A和B都是 D)以上都不是
解决方案:(A)
第一个差分表示为 xt = xt −xt−1. (1)
如我们所见,第一个差分消除了线性趋势。第二个差分(即(1)的差分)可以消除二次趋势,依此类推。
34)以下哪种交叉验证技术更适合时间序列数据?
A)k-折交叉验证 B)留一法交叉验证 C)Stratified Shuffle Split交叉验证 D)前向链交叉验证
解决方案:(D)
时间序列是有序数据。因此,必须对验证数据进行排序。前向链可确保这一点。其工作方式如下:
fold 1:训练[1],测试[2]
fold 2:训练[1 2],测试[3]
fold 3:训练[1 2 3],测试[4]
fold 4:训练[1 2 3 4],测试[5]
fold 5:训练[1 2 3 4 5],测试[6]
35)BIC比AIC更能惩罚复杂的模型。
A)真 B)假
解决方案:(A)
AIC = -2 * ln(likelihood)+ 2 * k,
BIC = -2 * ln(likelihood)+ ln(N)* k,
当:
k = 模型自由度
N = 观察数
在N相对较低时(7及以下),BIC比AIC更能容忍自由参数,但在N相对较高时则容忍度较低(因为N的自然对数大于2)。
36)下图显示了n = 60个观测值的时间序列的估计自相关和部分自相关。基于这些图,我们应该____.

A)通过获取日志来转换数据 B)对序列求差分以获取平稳数据 C)将MA(1)模型拟合到时间序列
解决方案:(B)
自相关显示出确定的趋势,而部分自相关显示出波动的趋势,在这种情况下,采用对数是没有用的。对序列求差分以获得平稳序列是唯一的选择。
37-38
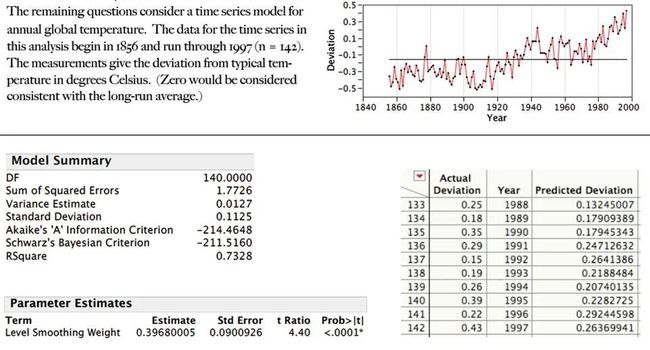
37)使用上面给出的估计指数平滑度,并预测接下来3年(1998-2000年)的温度
这些结果总结了简单指数平滑与时间序列的拟合。
A)0.2,0.32,0.6 B)0.33,0.33,0.33 C)0.27,0.27,0.27 D)0.4,0.3,0.37
解决方案:(B)
指数平滑的预测值在3年中都是相同的,因此我们所需要的只是明年的值。平滑的表达式是
smootht = α yt + (1 – α) smooth t-1
因此,对于下一个点,平滑的下一个值(下一个观察的预测)为
smoothn = α yn + (1 – α) smooth n-1
= 0.39680.43 + (1 – 0.3968) 0.3968
= 0.3297
38) 找出1999年气温预测的95%预测区间。
「这些结果总结了简单指数平滑对时间序列的拟合。」
A)0.3297 2 * 0.1125 B)0.3297 2 * 0.121 C)0.3297 2 * 0.129 D)0.3297 2 * 0.22
解决方案:(B)
预测误差的标准偏差为
1个周期为 0.1125
2个周期为 0.1125 sqrt(1+α2) = 0.1125 * sqrt(1+ 0.39682) ≈ 0.121
39)以下哪个陈述是正确的?
如果ARIMA模型中的自回归参数(p)为1,则表示序列中不存在自相关。
如果ARIMA模型中的移动平均成分(q)为1,则表示序列中具有滞后1的自相关
如果ARIMA模型中的积分成分(d)为0,则意味着系列不是平稳的。
A)仅1 B)1和2均 C)仅2 D)所有陈述
解决方案:(C)
自回归分量:AR代表自回归。自回归参数由p表示。当p = 0时,表示序列中不存在自相关。当p = 1时,表示序列自相关到一个滞后。
积分:在ARIMA时间序列分析中,积分用d表示。积分是微分的倒数。
当d = 0时,这意味着级数是平稳的,我们不需要取其差。
当d = 1时,这意味着该序列不是平稳的,并且要使其平稳,我们需要求第一差分。
当d = 2时,表示序列需要二次差分。
通常情况下,两个以上的差分是不可靠的。
移动平均分量:MA表示移动平均,用q表示。在ARIMA中,移动平均q = 1表示它是一个误差项,并且存在一个滞后的自相关。
40)在时间序列预测问题中,如果第1、2和3季度的季节指数分别为0.80、0.90和0.95。你对第四季度的季节性指数有何看法?
A)小于1 B)大于1 C)等于1 D)季节性不存在 E)数据不足
解决方案:(B)
由于有四个季度,所以季节指数必须总计为4。0.80 + 0.90 + 0.95 = 2.65,因此对于4的季节指数个季度必须是4-2.65 = 1.35,所以B是正确的答案。
原文链接:https://www.analyticsvidhya.com/blog/2017/04/40-questions-on-time-series-solution-skillpower-time-series-datafest-2017
![]()
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑获取一折本站知识星球优惠券,复制链接直接打开:https://t.zsxq.com/yFQV7am本站qq群1003271085。加入微信群请扫码进群: