实验八---有向不带权图的遍历以及简单路径的求解

【目的】
1. 领会图的两种存储结构和图的基本运算算法设计；领会图的两种遍历算法。
2. 掌握图的深度优先遍历和广度优先遍历算法在求解图路径搜索问题中的应用。

**
【内容】
**建立有向图的邻接矩阵和邻接表存储结构，并实现两种遍历运算、简单路径求解：
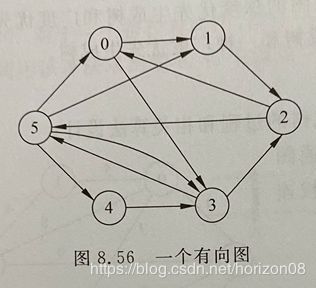
(1)建立如图8.56所示的有向图G的邻接矩阵和邻接表存储结构，并输出这两种结构。
(2)根据邻接表，实现图G的从顶点0开始的深度优先遍历和广度优先遍历运算。
(3)根据邻接表，输出：
①从顶点5到顶点2的所有长度为3的
简单路径；
②从顶点5到顶点2的最短路径。
(4)销毁图G的邻接表。

#include 
#include 
#include 
#include 
#define ElemType int
#define maxsize 100
#define InfoType int
#define MAXV 100
#define MaxSize 100
#define INF 214748364 ///一定不要设成int的最大值，因为后面的floyd算法会进行加法运算，会导致结果溢出变成负值，int_max=2147483647
#define INFINITE INF
/////////////////////////////////////////////////
//邻接表的结构体定义
typedef struct ANode
{
    int adjvex;            //该边的邻接点的编号，即有向边指向的顶点编号
    struct ANode *nextarc; //指向下一条边的指针
    int weight;            //边的相关的信息，如权值
} ArcNode;                 //边节点的类型

typedef struct Vnode
{
    InfoType info;     //顶点的其他信息
    int count;         //存放顶点入度
    ArcNode *firstarc; //指向第一个边节点
} VNode;               //邻接表的头节点的结构体类型

typedef struct
{
    VNode adjlist[MAXV]; //头节点的数组
    int n, e;            //图的顶点数和边数
} AdjGraph;              //整个邻接表的数据结构体类型
//////////////////////////////////////////////////
//邻接矩阵的结构体
typedef struct S
{
    int no;        //顶点的编号
    InfoType info; //顶点的其他信息
} VertexType;      //顶点的类型

typedef struct SS
{
    int edges[MAXV][MAXV]; //邻接矩阵的数组
    int n, e;              //图的顶点数和边数
    VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
///////////////////////////////////////////////////
typedef struct SSS
{
    ElemType data[maxsize];
    int front;
    int rear;
} SqQueue; //队列的结构体
////////////////////////////////
//Kruskal算法需要的简化图的结构体
typedef struct head
{
    int u; //边的起始顶点
    int v; //边的终止顶点
    int w; //边的权值
} Edge;
///////////////////////////////

int visited[MAXV] = {0};
///////////////////////////////
//队列的操作函数集合
//由于队列的函数在另一个文件
//所以需要声明一下
void InitQueue(SqQueue *&q);
void DestoryQueue(SqQueue *&q);
bool QueueEmpty(SqQueue *q);
bool enQueue(SqQueue *&q, ElemType e);
bool deQueue(SqQueue *&q, ElemType &e);
/////////////////////////////////////////////////////////////////
//后序遍历需要的一些队列的基本函数
void InitQueue(SqQueue *&q)
{
    q = (SqQueue *)malloc(sizeof(SqQueue));
    q->front = q->rear = 0;
}

void DestoryQueue(SqQueue *&q)
{
    free(q);
}

bool QueueEmpty(SqQueue *q)
{
    return (q->front == q->rear);
}

bool enQueue(SqQueue *&q, ElemType e)
{
    if ((q->rear + 1) % maxsize == q->front)
        return false;
    q->rear = (q->rear + 1) % maxsize;
    q->data[q->rear] = e;
    return true;
}

bool deQueue(SqQueue *&q, ElemType &e)
{
    if (q->front == q->rear)
        return false;

    q->front = (q->front + 1) % maxsize;
    e = q->data[q->front];

    return true;
}
/////////////////////////////////////////////////////////////////
void Dispath(MatGraph g, int dist[], int path[], int s[], int v);


void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
    int i, j;
    ArcNode *p;
    G = (AdjGraph *)malloc(sizeof(AdjGraph));
    for (i = 0; i < n; i++)
        G->adjlist[i].firstarc = NULL;

    for (i = 0; i < n; i++)
        for (j = n - 1; j >= 0; j--)
            if (A[i][j] != 0 && A[i][j] != INF)
            {
                p = (ArcNode *)malloc(sizeof(ArcNode));
                p->adjvex = j;
                p->weight = A[i][j];
                p->nextarc = G->adjlist[i].firstarc;
                G->adjlist[i].firstarc = p;
            }
    G->n = n;
    G->e = e;
}

void DispAdj(AdjGraph *G) //输出邻接表G
{
    int i;
    ArcNode *p;
    for (i = 0; i < G->n; i++)
    {
        p = G->adjlist[i].firstarc;
        printf("%3d: ", i);
        while (p != NULL)
        {
            if (p->weight != 2147483647) //2147483647
                printf("%3d[%d]→", p->adjvex, p->weight);
            p = p->nextarc;
        }
        printf("∧\n");
    }
}

void DestroyAdj(AdjGraph *&G) //销毁邻接表
{
    int i;
    ArcNode *pre, *p;
    for (i = 0; i < G->n; i++) //扫描所有的单链表
    {
        pre = G->adjlist[i].firstarc; //p指向第i个单链表的首结点
        if (pre != NULL)
        {
            p = pre->nextarc;
            while (p != NULL) //释放第i个单链表的所有边结点
            {
                free(pre);
                pre = p;
                p = p->nextarc;
            }
            free(pre);
        }
    }
    free(G); //释放头结点数组
}

/////////////////////////////////////////////////////////////////////
//遍历的两种算法巴拉巴拉巴拉
//邻接表的链式深度优先遍历算法
void DFS(AdjGraph *G, int v)
{
    ArcNode *p;
    visited[v] = 1;
    printf("%d ", v);
    p = G->adjlist[v].firstarc;
    while (p != NULL) //为了把p的指向的下面节点全部遍历
    {
        if (visited[p->adjvex] == 0)
            DFS(G, p->adjvex);
        p = p->nextarc;
    }
}
//邻接表的链式广度优先遍历算法
void BFS(AdjGraph *G, int v)
{
    int w, i;
    ArcNode *p;
    SqQueue *qu;
    InitQueue(qu);
    int visited[MAXV];

    for (i = 0; i < G->n; i++)
        visited[i] = 0;

    printf("%2d", v);
    visited[v] = 1;

    enQueue(qu, v);

    while (!QueueEmpty(qu))
    {
        deQueue(qu, w);
        p = G->adjlist[w].firstarc;
        while (p != NULL)
        {
            if (visited[p->adjvex] == 0)
            {
                printf("%2d", p->adjvex);
                visited[p->adjvex] = 1;
                enQueue(qu, p->adjvex);
            }
            p = p->nextarc;
        }
    }
    printf("\n");
}

/////////////////////////////////////////////////////////////////////////////////////////
//邻接表转化成邻接矩阵的函数
//该函数也可以变成一个构造邻接矩阵的函数
void ListToMat(AdjGraph *G, MatGraph &g)
{
    int i;
    ArcNode *p;

    for (i = 0; i < G->n; i++) //扫描每一个头节点顶点
    {
        p = G->adjlist[i].firstarc;
        while (p != NULL) //找到后接着寻找头节点的后继边节点
        {
            g.edges[i][p->adjvex] = p->weight;
            p = p->nextarc;
        }
    }
    g.n = G->n;
    g.e = G->e;
}

//输出邻接矩阵的函数
void DispMat(MatGraph g)
{
    int i, j;
    printf("\n该图的顶点数%d，边数是%d\n\n", g.n, g.e);
    for (i = 0; i < g.n; i++)
        for (j = 0; j < g.n; j++)
        {
            if (i == j)
                printf(" (%d, %d)的权值为0 \n", i, j);
            else if (g.edges[i][j] == INF)
                printf(" (%d, %d)的权值为INF \n", i, j);
            else
                printf(" (%d, %d)的权值为%d \n", i, j, g.edges[i][j]);
        }
}
//////////////////////////////////////////////////////////////////////////////
//基于深度优先遍历算法的应用
//主要是应用在寻找简单路径的和特定的长度的简单路径的应用上
//////////////////////////////////////////////
//求解对应u，v的全部简单路径（即顶点不重复的路径）
void FindAllPath(AdjGraph *G, int u, int v, int path[], int d)
//d表示path【】路径长度，初始值设为-1
{
    int w, i;
    ArcNode *p;
    d++;
    path[d] = u;
    visited[u] = 1;
    if (u == v && d >= 0)
    {
        for (i = 0; i <= d; i++)
            printf("%2d", path[i]);
        printf("\n");
    }

    p = G->adjlist[u].firstarc;
    while (p != NULL)
    {
        w = p->adjvex;
        if (visited[w] == 0)
            FindAllPath(G, w, v, path, d);
        p = p->nextarc;
    }
    visited[u] = 0;
}
/////////////////////////////////////
//寻找从u到v的所有路径长度为l的简单路径
void PathlenAll(AdjGraph *G, int u, int v, int l, int path[], int d)
{
    int w, i;
    ArcNode *p;
    visited[u] = 1;
    d++;
    path[d] = u;

    if (u == v && d == l)
    {
        printf(" ");
        for (i = 0; i <= d; i++)
            printf("%2d", path[i]);
        printf("\n");
    }

    p = G->adjlist[u].firstarc;
    while (p != NULL)
    {
        w = p->adjvex;
        if (visited[w] == 0)
            PathlenAll(G, w, v, l, path, d);
        p = p->nextarc;
    }
    visited[u] = 0;
}

//////////////////////////////////////////////////////////////////////////////

int main()
{
    AdjGraph *G;
    MatGraph g;

    int n = 5, e = 6, i, j;
    int path[10];
    int A[10][MAXV] = ////有向带权的连通图
        {{0, 6, INF, INF, INF},
         {INF, 0, 1, INF, INF},
         {INF, INF, 0, 3, 2},
         {INF, INF, INF, 0, INF},
         {5, INF, INF, 2, 0}};

    int B[6][MAXV] = {
        {0, 1, 0, 1, 0, 0},
        {0, 0, 1, 0, 0, 0},
        {1, 0, 0, 0, 0, 1},
        {0, 0, 1, 0, 0, 1},
        {0, 0, 0, 1, 0, 0},
        {1, 1, 0, 1, 1, 0}};

    CreateAdj(G, B, 6, 12); //创建图的邻接表
    printf("G的邻接表:\n");
    DispAdj(G);

    for (i = 0; i < 6; i++) //初始化邻接矩阵，防止异常
        for (j = 0; j < 6; j++)
            g.edges[i][j] = 0;

    printf("利用邻接表生成邻接矩阵\n");
    ListToMat(G, g);
    for (i = 0; i < 6; i++)
    { //初始化邻接矩阵，防止异常
        for (j = 0; j < 6; j++)
            printf("(%d,%d) = %d     ", i, j, g.edges[i][j]);
        printf("\n");
    }
    // DispMat(g);
    printf("邻接表从0开始的深度优先遍历算法:\n");
    DFS(G, 0);

    printf("\n邻接表从0开始的广度优先遍历算法:\n");
    BFS(G, 0);

    for (int i = 0; i < 6; i++)
        visited[i] = 0;
    printf("\n 从5 到2 的全部的简单路径 \n");
    FindAllPath(G, 5, 2, path, -1);

    printf("\n 输出5 到2 的长度为3的路径 \n");
    PathlenAll(G, 5, 2, 3, path, -1);

    printf("\n销毁图G的邻接表\n");
    DestroyAdj(G);
    system("pause");
    return 0;
}

不要白嫖，记得点赞啊