邓俊辉版数据结构整理(4)：平衡二叉搜索树（AVL树）

节点数目固定时，兄弟子树高度越接近，全树也将倾向于更低。

由n个节点组成的二叉树，高度不低于，恰好为时，称为理想平衡。

高度渐进地不超过O()，即可称作适度平衡

zig旋转

zag旋转

平衡因子：

balFac(v) = height(lc(v)) - height(rc(v));左子树高度减右子树高度。

若树平衡，则   -1 =< balFac(v) =< 1;

若树因为插入或删除节点，使树不再平衡(平衡因子不再满足平衡条件)，则可以通过旋转（单旋，双旋）使树重新达到平衡

单旋：

一次zig或者一次zag旋转

同时可有多个失衡节点，最低者g不低于x祖父；

g经单调旋转后复衡，子树高度复原；更高祖先也必平衡，全树复衡；

双旋：

zig和zag旋转合并使用，zigzag或者zagzig。

插入算法：（调整平衡）

插入引起的不平衡，只会影响到祖父节点。所以代码中一旦if(!AvlBalanced(*g))为true，则此节点为最低节点，即grandparent。

所以调整一次平衡后，可以退出for循环。

rotateAt()方法 实现在 3+4重构 小节

template  BinNodePosi(T) AVL::insert(const T & e)
{
  BinNodePosi(T) hot;
  BinNodePosi(T) & v; //树根节点
  BinNodePosi(T) & x = search(v, e, hot);
  if(x) return x;//目标已经存在
  x = new BinNode(e, hot);//目标不存在,创建x
  size ++;
  BinNodePosi(T) xx = x;
  //从x父亲出发，逐层向上，依次检查各代祖先g
  for(BinNodePosi(T) g = x->parent; g; g = g->parent)
  {
    if(!AvlBalanced(*g)) //一旦发现失衡则通过调整恢复平衡，不平衡，
    {
      FromParentTo(*g) = rotateAt(tallerChlid(tallerChild(g)));
      break;//g复衡后，局部子树高度必然复原；其祖先亦必如此，故调整结束
    }
    else//依然平衡，
    {
      updateHeight(g);//更新高度(平衡性虽不变，但是高度改变)
    }
    return xx;  //返回新节点
  }
}

删除算法：（调整平衡）

删除引起的不平衡，可能会顺序的影响历代祖先节点，所以需要顺序的遍历所有历代祖先节点。

rotateAt实现在 3+4重构 小节

template  bool AVL::remove(const T & e)
{
  BinNodePosi(T) & x = search(e);
  if(!x) return false;//若目标不存在
  removeAt(x, hot); size --;//则按BST规则删除后，hot及其祖先均有可能失衡
  //以下，从hot出发逐层向上，依次检查各代祖先g
  for(BinNodePosi(T) g = hot; g; g = g->parent)
  {
    if(!AvlBalanced(*g))//一旦发现g失衡，则通过调整恢复平衡
    {
      g = FromParentTo(*g) = rotateAt(tallerChlid(tallerChlid(g)));
    }
    updateHeight(g);//  并更新其高度
  }//可能需做过logn次调整，无论是否做过调整，全树高度均有可能下降
  return true;
}

3+4重构：（rotateAt算法分析及实现）

zig旋转，zag旋转，单旋，双旋，只是为了我们便于理解树的变形，算法实现起来并不是如此，用的是如下方法。

• 设g(x)为最低的失衡节点，考察祖孙三代：g～p～v，按中序遍历顺序将其命名为a～b～c；
• 它们总共拥有不相交的四棵子树（可能为空的），按照终须遍历顺序将其重命名为：

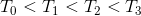
表现形式如下：

重新组织三个节点与子树的算法如下：

template  BinNodePosi(T) BST::connect34(BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c,
      BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3)
{
  a->lChlid = T0; if(T0) T0->parent = a;
  a->rChlid = T1; if(T1) T1->parent = a;
  updateHeight(a);
  c->lChlid = T2; if(T2) T2->parent = c;
  c->rChlid = T3; if(T3) T3->parent = c;
  updateHeight(c);
  b->lChlid = a; a->parent = b;
  b->rChlid = c; c->parent = b;
  updateHeight(b);
  return b;//该子树新的跟节点
}

rotateAt算法实现：

template  BinNodePosi(T) BST::rotateAt(BinNodePosi(T) v)
{
  BinNodePosi(T) p = v->parent, g = p->parent;//父亲，祖父
  if(IsLChlid(*p))//zig
  {
    if(IsLChlid(*v))//zig-zig
    {
      p->parent = g->parent;
      return connect34(v, p, g, v->lChlid(), v->rChild(), p->rChlid(), g->rChlid());
    }
    else//zig-zag
    {
      v->parent = g->parent;
      return connect34(p, v, g, p->lChlid(), v->lChlid(), v->rChlid(), g->rChlid());
    }
  }
  else//IsRChlid(*p) zag
  {
    if(IsRChlid(*v))//zag-zag
    {
      p->parent = g->parent;
      return connect34(g, p, v, g->lChlid(), p->lChild(), v->lChlid(), v->rChlid());
    }
    else//zag-zig
    {
      v->parent = g->parent;
      return connect34(g, v, p, g->lChlid(), v->lChlid(), v->rChlid(), g->rChlid());
    }
  }
}

四种情况图鉴：

zig-zig:

zig-zag:

zag-zag:

zag-zig: