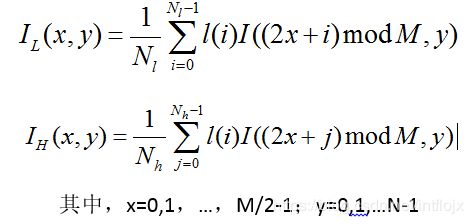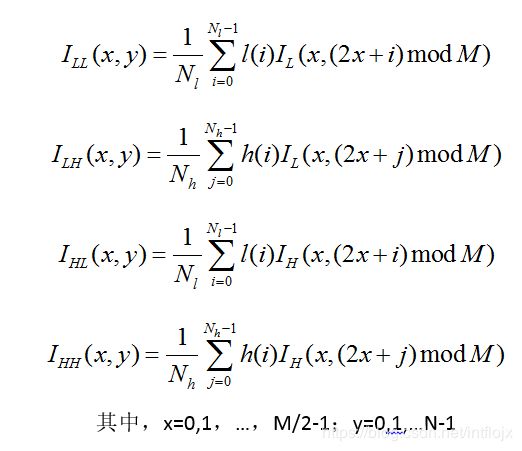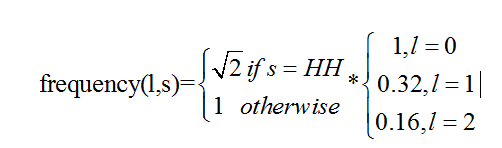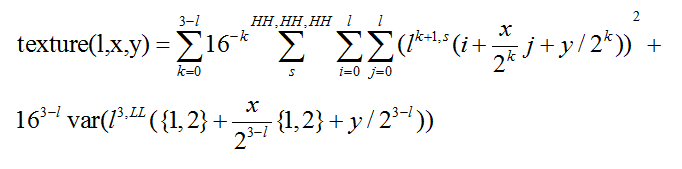最小可觉察误差(JND)与图像压缩

 1. JND算法背景/意义

1. 1算法的概述

最小可觉察误差(JND, Just Noticeable Distortion)用于表示人眼不能察觉的最大图像失真，体现了人眼对图像改变的容忍度。在图像处理领域，JND 可以用来度量人眼对图像中不同区域失真的敏感性。目前已有多个 JND 模型被提出，这些 JND 模型主要可以分为 2 类：基于像素域的 JND模型和基于变换域的 JND 模型。

像素域 JND 模型能在像素域上更为直观地给出 JND 阈值，在视频编码时常常用于运动估计以及预测残差的滤波。主要方法有：

1. Yang 等人提出了经典的非线性相加掩蔽模型(NAMM, nonlinear additively masking model)：该方法兼顾了亮度自适应掩蔽和对比度掩蔽的重叠效应。
2. Liu 等人在 NAMM 模型的基础上，通过全变分（ TV, total variation）分解对图像中的纹理以及结构分量赋以不同加权值，使像素域JND 模型具有更好的计算精度。
3. Wu 等人则在计算纹理掩盖时进一步考虑了人眼对规则区域与非规则区域不同的敏感性，提出一种基于亮度自适应与结构相似性的JND 模型。

在变换域中，人类视觉系统 HVS 的某些特性可以方便地结合到应用中，以增强算法的整体性能。比如变换域的JND模型可以方便地把对比度敏感函数（CSF, contrast sensitivity function）引入模型中，具有较高的精度。变换域JND 模型又可以分为基于DCT域的 JND模型以及基于DWT域的JND模型。

1. Ahumada 等人通过计算空域CSF 函数得到灰度图像的 JND 模型。
2. Watson 提出了 DCTune 方法，进一步考虑了亮度自适应、对比度掩蔽等特性对 JND 的影响。
3. Zhang等人通过加入亮度自适应因子和对比度掩蔽因子，使得 JND 模型具有更高的精度。
4. Jia 等人将物体的运动等因素引入到 JND 模型中， 提出了一种更精确的视频图像 JND 模型。
5. Wei 等人则将伽马校正引入到 JND 模型， 提出新的亮度自适应和对比度掩蔽因子计算方法。
6. Ma 等人在 Wei 的基础上提出自适应块大小的 JND 模型，将通常 8×8 尺寸的 JND
   模型扩展到 16×16。
7. Luo 等人把 Wei 的 JND模型推广到 4×4，并用于扩展基于 H.264 的视觉特性视频编码。

1. 刘静,王永芳,武翠芳,张兆杨. 改进的JND模型及其在图像编码中的应用[J]. 电视技术,2011,13:15-18.
2. 郑明魁,苏凯雄,王卫星,兰诚栋,杨秀芝. 基于纹理分解的变换域JND模型及图像编码方法[J]. 通信学报,2014,06:185-191+199.

 

算法的意义

传统的图像/视频编码技术主要针对空间域冗余、时间域冗余以及统计冗余进行压缩编码， 但很少考虑到人眼视觉系统特性和心理效应， 因此大量视觉冗余数据被编码并传输， 为了进一步提高编码的效率， 研究人员开始了致力于去除视觉冗余的研究。目前一个表征视觉冗余的有效方法就是基于心理学和生理学的最小可察觉失真模型， 即人眼不能感知的变化， 由于人眼的各种屏蔽效应， 人眼只能觉察超过某一阈值的噪声， 该阈值就是人眼的恰可觉察。

算法适用范围

JND模型常用来指导图像或视频的感知编码和处理， 如预处理、 自适应量化、 码流控制、 运动估计等。近年来， JND 模型在基于视觉特性的视频图像编码、数字水印、图像质量评价等方面受到广泛关注。

 

1. 郑明魁,苏凯雄,王卫星,兰诚栋,杨秀芝. 基于纹理分解的变换域JND模型及图像编码方法[J]. 通信学报,2014,06:185-191+199.
2. 元家昕,马允胜. 基于人眼JND门限的多分辨率水印嵌入算法[J]. 计算机工程与应用,2006,08:63-65+95.
3. 束道胜. 基于JND模型的视频压缩算法研究[D].安徽大学,2013.

1. 算法原理分析
   1. 算法框架/流程

考虑到ROI和SPECK算法都在小波域进行，重点考虑基于DWT域的 JND模型。目前的图像视频编码标准主要建立在香农信息论基础之上，用概率统计模型描述信源，其压缩思想主要从去除数据冗余方面出发，如果考虑视觉上的冗余特性。人眼对不同类别区域的敏感度不同，因此可以将体现敏感程度的JND 阈值结合到量化过程中，在不同敏感区域使用不同的量化步长。

最后就能保证压缩的不可察觉性。

DWT 域中最常见的视觉模型是文献[6]描述的 JND模型 ，其 JND 阈值的计算方法如下:

整体框架为:

 

图2-1 系统总体流程图

1. 肖亮，韦志辉，吴慧中. 一种利用人眼视觉掩盖的小波域数字水印[J]. 通信学报，2002，23(3):100-106.
   1. 图像小波变换步骤
      1. 图像小波变换具体原理分析

它是一种时频变换分析方法，将信号展开成一族基函数（小波）加权之和，通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。与变换域相比，小波变换具有良好的能量集中特性，其良好的时频分解特性更符合人类视觉系统的特点。

图像经过小波变换后生成的小波图像的数据总量与原图像的数据量相等，即小波变换本身并不具有压缩功能。之所以将它用于图像压缩，是因为生成的小波图像具有与原图像不同的特性，表现在图像的能量主要集中于低频部分，而水平、垂直和对角线部分的能量则较少；水平、垂直和对角线部分表征了原图像在水平、垂直和对角线部分的边缘信息，具有明显的方向特性。低频部分可以称为亮度图像(近似图像)，水平、垂直和对角线部分可以称为细节图像。人眼对亮度图像（低频）部分的信息特别敏感，对这一部分的压缩应尽可能减少失真或者无失真，其它部分可以用允许失真来提高压缩率。

 

 

图2-4 图像经三级小波变换示意图

1. 1. 1. 多分辨率理论

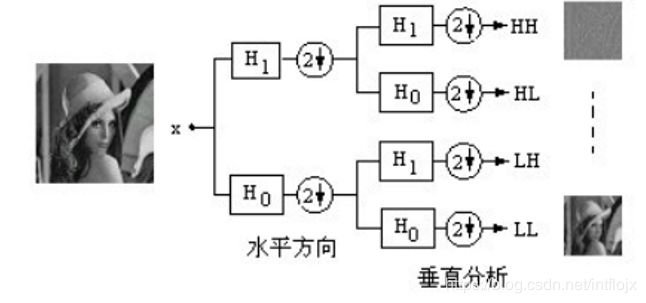
任何共轭滤波器都可以用来刻画一种小波，它能产生实数空间中的正交基，而且快速离散小波变换何以串联这些共轭镜像滤波器来实现。这就是著名的Mallat快速算法,它把小波分解与多采样滤波器组联系起来,并且符合人体视觉系统对各频段的视觉敏感特性。Mallatt算法是是一种求解小波系数的塔形算法思想，对一幅图像完成一次一维小波变换，需要对图像的行和列分别进行一次水平和垂直滤波。小波变换将原始图像分成4个子带，即1个低频子带(LL)与3个高频子带(LH，HL，HH)。如图所示为二维图像的(一级)分解。

令I(x,y)表示大小为M*N的原始图像，L(i)表示相对于小波变换的低通滤波器系数，i=0,1,2,..Nl-1, Nl表示滤波器L的支撑长度。H(i)表示相对于小波变换的高通滤波器系数，i=0,1,2,..Nh-1, Nh表示滤波器H的支撑长度。

其中，x=0,1，…，M/2-1；y=0,1,…N-1

得到如下四个表达式

 

 

 

其中，x=0,1，…，M/2-1；y=0,1,…N-1

图2-5 Mallat快速算法的图像小波变换

1. 1. 1. 小波变换总结
2. 小波变换是后续算法的基础，不可省却。
3. 小波变换能进行多分辨分析，同时兼顾时频域特性。小波变换是时间（空间）频率的局部化分析，通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频时间细分，低频处频率细分，能自动适应视频信号分析的要求，从而可聚焦到信号的任意细节。能克服传统傅里叶变换、短时傅里叶变换、余弦变换的缺点。（不会产生马赛克模糊）
4. Mallat提出用共轭镜像滤波器来刻画小波，实现小波变换，小波变换变成信号的滤波过程。图像可以看做二维信号，对行和列分别进行一次水平和垂直滤波，小波变换将原始图像分成4个子带，同时可以做多尺度分析。
5. 经过小波变换之后，有效将图像近似值和细节部分。可以通过减少细节部分的刻画实现压缩。

改进方向

1. 提升结构的可逆整数小波变换：SPECK 采用的是离散小波变换，即第一代小波变换，该变换运算量较大，产生的是浮点数，由于计算机有限字长的影响，往往不能精确重构信号，同时也浪费了大量的时间。而整数小波变换（提升方法）不仅继承了第一代小波的多分辨率分析的优点，而且逆变换实现简单、快速和直接，能够很好地实现信号的重构。

图2-6 提升结构的小波变换示意图

[7] 朱锦华，许茹，陈华宾《给予提升小波变换的SPECK图像编码算法》

1. 小波包分解作为小波分解的金字塔结构的推广，在高频子带也进行小波迭代分解。自适应分解产生的小波包子带结构，在小波分解基础上高频系数具有更强的能量聚集性和较高的编码率失真性能，因此图像压缩效率要优于传统的金字塔结构，尤其是对于纹理丰富的图像。小波包分解在小波分解的高频子带继续迭代分解，让高频的能量具有更强的聚集性，而且高频子带系数在左上角存在重要系数的可能性大大高于其它位置。基于以上分析，提出适合小波包子带中 S 集合的一种新的分裂方式。

[8] 张岩，聂永丹，唐国维《一种基于小波包变换的 SPECK 图像编码算法》，2012年10月

1. 1. JND阈值求解

在JND模型中，主要考虑，frequency （频率），luminance（F:\JND\JND_img），texture (纹理)的综合影响。

如果对原始图像进行1层小波变换。人类视觉系统对图像第l个频带上方向为s的频率敏感度为

人类视觉系统对像素点（x，y）的亮度敏感性可由下式 表示

像素点(x,y)所在的区域的纹理复杂度可由下式表示

1. 1. 原理类似的其他算法

3.1.1与JPEG算法对比（有优势）

（1）JPEG在图像区块编码采用DCT（离散余弦变换），SPECK采用的是DWT（离散小波变换）。DCT相比DWT有劣势，需要将图像分为8*8或者16*16的块（常见的两种），这样随着压缩率的增加，会产生块效应。图像边缘变得模糊，产生“马赛克”失真，约束了图像压缩率。

（2）采用SPECK在Internet图像浏览和传输上，提供质量、分辨率上图像渐进式的分级结构更有优势。

（3）JPEG目前应用广泛，SPECK目前较少。

（4）SPECK编码时间长于JPEG。

3.1.2与JPEG2000算法对比

（1）同样采用小波变换

（2）JPEG2000核心算法是EBCOT，采用两重编码，压缩比例更高。

（3）JPEG2000时间复杂性更大。

1. 1. 算法适用范围类似的其他算法

/* 1. 有哪些算法跟该算法的适用范围是类似的？2. 该算法与其他类似的算法有什么优势或者劣势？ */

3.2.1在图像变换上与DCT变换类似

对于传统的DCT块变换，小波变换具有以下优点： 

1. 具有熵保持特性，能够有效地改变图像的能量分布，同时不损伤原始图像所包含的信息。
2. 分解后大部分能量集中在低频子带的少量系数上，而大量的高频子带系数值普遍较小，且存在明显的相关性，有利于获得较高的编码效益。
3. 小波变换作用于图像的整体，既能去除图像的全局相关性，又可将量化误差分散到整个图像内，避免了方块效应的产生。 
4. 多级分解后形成的不同分辨率的频率特性的子带信号，便于在失真编码中综合考虑视觉特性，同时有利于图像的渐进传输。

3.2.2图像编码方式对比

1. 行长编码：擅长于重复数字的压缩。

1. Huffman编码：擅长于像素个数分布不均匀情况下的编码。
2. 算术编码：适合分布概率相同的压缩。

可以通过编码数据的特点选择最佳的编码方式。

3.2.3 其他几种嵌入式编码对比

EZW算法是一种基于零树的嵌入式图象编码算法，虽然在小波变换系数中，零树是一个比较有效的表示不重要系数的数据结构，但是，在小波系数中还存在这样的树结构，它的树根是重要的，除树根以外的其它结点是不重要的。对这样的系数结构，零树就不是一种很有效的表示方法。根据基本思想，提出了一种新的且性能更优的实现方法，即基于多级树集合分裂排序（SPIHT）的编码算法。它采用了空间方向树表述系数结构，从而提高编码效率。而SPECK在EZW的基础上，利用小波系数分布特点，使得重要的小波系数优先被编码。SPIHT和EZW只能等前一棵数编码完毕才能进行下一棵数的编码，误码将影响整个树的结构，SPECK算法块之间可以独立编码，对整个图像还原不造成影响。是近期嵌入式分级图像编码算法中性能较好的一种，其中最主要的操作仅包含对小波系数幅值和阈值的比较判断，因此计算复杂度低，运行效率高，并能达到与 EZW、SPIHT 算法相似或更好的编码效率。

附录

yang

zhou

图1 基于像素域的JND变换

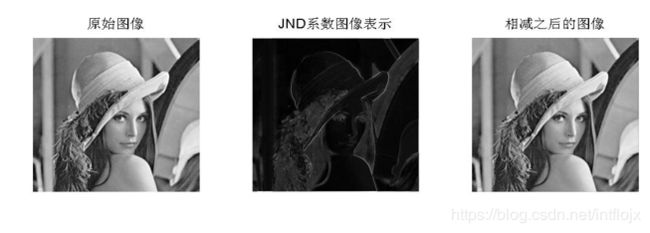
JND求解结果灰度图，头发等条纹复杂的JND系数高，平滑区域比较暗，结果合理。

图2 基于小波域的JND变换

SPECK算法（参数可调）