线性回归算法拟合数据原理分析以及源代码解析
线性回归算法拟合数据原理分析以及源代码解析
前言
前面的博客讲的都是分类问题,接下来的几篇博客,会着重于回归,倾向于对数据进行预测。大家是不是一听到预测就眼睛一闪,是不是可以用来预测股票涨跌、彩票号码什么的!我只能告诉你有人做出来的股票预测软件,而且正确率挺可观的。作为一个学习者,别着急,千里之行始于足下。踏踏实实的从原理到代码,一步一脚印。
项目源码已上传至GitHubb上,有需要的自取:项目地址
如果项目对你有些许帮助,不要忘记给个小⭐⭐
线性回归原理以及公式
1. 简单知识回顾
二元一次方程式大家都已经非常熟悉了,下面这个是他的一般式【式子1】:
不过通常呢,我们会将这个一般式中的y单独拿到等式一侧,其余的放在另一侧【式子2】:
注意,这两个式子的a和b不是一回事,各自表示对应式子的系数或者常数。
我们都知道,对于式子2来讲,决定这个式子在图像中的显示位置的是系数a,和常数b。
对于图上这张图来说,红色这条直线对应的二元一次方程式子2的系数a为2,b为-1.蓝色这条线对应的式子2的系数a为-1,b为5.
也就是说,只要给出a和b的值,那么,我就能画出这样一条直线。
那这跟我们的算法有什么关系呢?
说到的,我们就是针对数据,找出这样的a和b,以此得出一条直线方程。
本次呢,主要是针对单属性数据量做算法介绍,针对多属性值数据来讲, 道理相同,无非就是将数据2的系数a和变量x变成向量,同时对于常量b,我们也可以写道向量里。也就相当于下面公式:
这里的n表述数据的属性个数,m表示数据量。
2. 最小二乘法解二元一次方程
首先我们得先了解一下最小二乘法的原理,先看一下下面这张图:
图中浅蓝色的点是我们真实数据点的位置,黄色点是预测的数据点,中间这个绿色直线就是我们所
拟合出来的直线。预测点和真实数据点之间的距离,我们称之为误差。我们假设这条直线方程:
那么,针对这个误差,我们使用误差平方和来表示(其好处是能够解决正负值相互抵消问题):
为了达到更好的拟合效果,我们需要这个误差平方和达到最小。理想情况下,所有数据点均在拟合直线上,那么此时,这个误差平方和为0.
在代码方面,我们通常会将累积求和公式,使用向量的形式来进行表示,下面,我们对上面的公式进行向量化书写:
和普通的二次方程求解一样,我们对α进行求导,并且令导数为0,即可得出α的取值,使得上述式子达到最小值:
这里能进行合并的原因是 Yt X α 是一个标量,也就是这个结果是一个数,所以它的转置等于其本身
接着对其进行求导:
我们令其等于0,可求出α的求解公式:
向量求导这一块,也是我薄弱的环节,文末会给出一些参考资料,大家可以去深入了解一下,一起学习!
源代码实战讲解
下面开始我们的代码实战:
1. 加载数据
首先我们先看一下文本数据的属性有哪些
图中最坐标红色方块是数据的常数1,用来求解常量,对应着就是我们前面公式的b。
中间黄色的是我们的属性值α1.
最右边白色的是我们数据的值,也就是y值。
我们来看一下数据的分布情况:
![]()
def LoadData(filename):
dataMat = []
labelMat = []
with open(filename) as f:
numFeat = len(f.readline().split('\t'))-1
for line in f.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
- 首先从文件中加载进来数据
- 获取数据的属性个数numFeat
- 将数据的属性值和y值分别放入到dataMat列表和labelMat列表中
2. 计算α的值
def standRegres(xArr,yArr):
xMat = np.mat(xArr);yMat = np.mat(yArr).T#由于原来形状是(1,199),所以这里需要转置
print("yMat",yMat.shape)#yMat (199, 1)
xTx = xMat.T*xMat
if np.linalg.det(xTx)==0.0:
print("false")
return
print("xtx.shape",xTx.shape)#形状:(2,2)
print("xTx.I",xTx.I)#矩阵的逆
print("xMat.T",(xMat.T).shape)
ws = xTx.I*(xMat.T*yMat)#(xMat.T*yMat)形状为(2,1)
return ws
- 直接使用我们前面推导的公式,就能够直接得出α的值,对应代码中的,就是ws。
- xTx.I 是对xTx.I求逆
- xMat.T是求其转置。
3. 原数据以及拟合直线显示
def showdata(xArr,yMat,ws):
fig = plt.figure()
ax = fig.add_subplot(111)
xCopy = xArr.copy()
xCopy.sort(0)
yHat = xCopy*ws
ax.scatter(xArr[:,1].flatten().tolist(),yMat.T[:,0].flatten().tolist(),s=20,alpha=0.5)
ax.plot(xCopy[:,1],yHat)
plt.show()
- 具体如何画图,不清楚的可以看一下这个专栏matplotlib画图
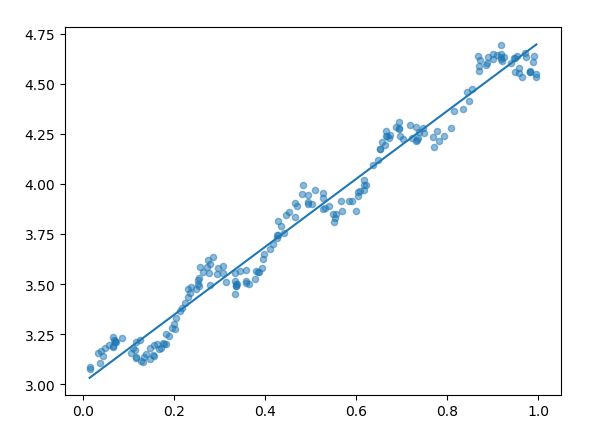
- 我们需要先对x进行排序,否则拟合直线无法正常显示
图中的直线就是我们所拟合的直线。
模型评价准则
任何一个模型都有适合它的评价准则,来判断这个模型的优良程度,那么,对于这个模型来说,我们使用的评价准则是Pearson相关分析,具体参考博客python数据分析-相关分析
总的就是用来评价两个变量之间的相关性程度,如果值接近1,表示强相关,如果接近于0,表示基本无关。
def pearsoncor(yHat,yMat):
result = np.corrcoef(yHat.T,yMat)#相关系数分析。越接近1,表示相似度越高
print("pearson-result:",result)
我们使用预测值和真实值进行相关系数分析,我们来看一下结果:
正对角线一定都是1,因为和自己的相关系数值一定为1
反对角线上的值就是预测值和真实值的相关系数。我们看到相关系数为0.98,表示我们拟合的直线与数据整体状态还是非常一致的。
总结
这里我们主要分析了一下线性回归对数据拟合的算法原理和代码,但是呢,会出现一个问题,就是会出现欠拟合。什么意思呢?就是拟合的直线无法很好的表现真实数据。那有没有改进方式呢,我们下一篇博客会讲到一种改进方法:局部加权线性回归
参考资料
- python数据分析-相关分析
- 向量求导
- 前导不变后导转置