【技术点】数据结构--二叉树之红黑树(三)
文章目录
- 前言
- 红黑树
- 为什么要有红黑树
- 红黑树的特征
- 新增节点
- 问题:如何判断用旋转还是用变色的手段来满足红黑树的规则?
- 最坏情况
- 删除
- 总结
- 下一步
前言
前面两篇文章:
【技术点】数据结构–二叉树(一)
【技术点】数据结构–二叉树(二)
讲了普通二叉树然后再到平衡搜索二叉树(BBST,Balance Binary Search Tree,又称AVL树)。
这一篇来讲讲更厉害(也就是更复杂)的一种树:红黑树(RBTree, Red Black Tree)。
红黑树
为什么要有红黑树
前面讲到的AVL树在搜索性能上已经达到了二分查找的性能:O(lgn)。
在插入时的性能也是最多两次旋转就可以调整完成,所以插入性能是 O(1)
那么为啥还有折腾一个红黑树出来呢?
我们回到上一篇文章,在上一篇文章讲删除节点的时候,我留了个问题:
foreach(node in allNode){ //新增节点后,计算所有节点的平衡因子,这有更好的算法,不需要每次都从头开始,这个不是这篇文章的内容,就按最简单的来写,最主要的是说明LL旋转
depth = getDeptInfo(node)
...
}
在删除的时候,把所有的节点的平衡因子全部计算一遍,看是否有需要调整的地方,当然这种笨办法不行。
实际上,删除一个节点,只会影响当前这边子树的平衡因子,因此,只需要从删除的这个因子往上找,一直找到根节点就可以了。那么,删除节点的性能就会是 O(lgn)
可以看下下面这棵树的删除过程:

由于删除7节点,造成了祖父节点6成为不平衡节点,因此需要做一次旋转。
我们的代码可以改成:
function delNodeToAVL(root, delNode){
parent = delNode.parent
del(root, delNode) //该函数就是将节点从树种删除,参考上一篇文章的内容
while(parent is not root){
depth = getDeptInfo(node)
if (depth > 1){
if (newNode.key < node.left.key){
ll_rotate(node)
}else if (newNode.key > node.right.key){
rr_rotate(node)
}else if (newNode.key > node.left.key){
rr_rotate(node)
ll_rotate(node)
}else if (newNode.key < node.right.key){
ll_rotate(node)
rr_rotate(node) //旋转是以不平衡节点来旋转的,不是root,所以这里应该还有其他处理步骤,懒得写了,也就是一些指针的调整了
}
parent = parent.parent
}
}
}
但是呢,如果一颗查询树的增删操作很多时,AVL树就有点力不从心了,大量的遍历和旋转操作暂用大量的时间,因此,红黑树就横空出世了。
红黑树的特征
红黑树首先是一个自平衡的二叉树,与AVL不同的是,红黑树的每个节点增加一个颜色属性:color,颜色或红色 (red) 或黑色 (black)。 红黑树除了有普通二叉查找树(BST)的一般特征外,还有如下特征:
- 规则1:节点是红色或黑色。
- 规则2:根节点是黑色。
- 规则3:所有叶子都是黑色,这里的叶子节点是空节点(NIL)
- 规则4: 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 规则5:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
来看看一颗典型的红黑树:

作为一颗平衡二叉树,搜索性能是O(lgn)。
我们来看一下怎样根据上面的原则来构建一颗红黑树。
新增节点
在新增节点时,为了达到接近二分查找的查找性能,和AVL树一样,我们会在新增节点之后,对树做一些调整操作,那么,红黑树的调整有两种方式:
- 变色
- 旋转
因为规则5的存在,假设一棵树已经是红黑树了,那么再加入新的节点时,如果新增黑色的节点,肯定会破坏规则导致调整,所以在实际中,我们引进规则6:
- 规则6:新插入的节点必须为红色。
通过一张图来看,插入数字顺序为 [5, 7, 9, 3, 1],每一个箭头为一步。
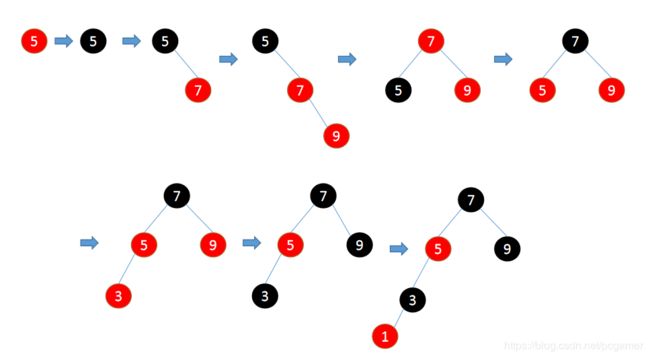
- 新增节点为5,为红色
- 新增节点为根节点,根据规则2,将节点变成黑色
- 增加节点7,为红色
- 增加节点9,为红色,违反规则4,此时无法通过变色来满足所有条件,所以我们使用旋转,为一次RR旋转
- 根据规则2,将节点7变成黑色,根据规则5,将节点5变成红色
- 增加节点3,为红色,违反规则4,此时我们选择变色,将节点3与其叔节点一起变色为黑色
- 增加节点1,此时就不平衡了,我们需要对齐进行平衡操作,有两种操作可以使树平衡,那就是 变色 + 旋转
这里有一个问题:
问题:如何判断用旋转还是用变色的手段来满足红黑树的规则?
这里可以分成两种情况:
- 情况1:新增节点的叔叔节点为红色,如图

那么我们对应的操作就可以是
A. 新增节点的父节点与叔叔节点的颜色变成黑色
B. 如果祖父节点为根节点,则不变化,否则祖父节点变成红色(如果不变,多出的一层黑色节点会破坏规则5)

- 情况2:叔叔节点为黑色
此时就需要进行旋转了,观察新节点、父节点、祖父节点的关系,来判断是LL/RR/LR/RL四种旋转之一。
A. 旋转(LL/RR/LR/RL之中的一种)
B. 旋转之后的新的root节点变成黑色,root的两个子树节点(如果是叶子就不变)变成红色。

根据上述的情况,我们可以判断写一段伪代码了:
function addNodeToRBT(root, newNode){
newNode.color = 'red'
addNode(root,newNode)
if (newNode.uncle = 'red'){ //获取uncle节点的方式有很多种
newNode.parent.color = 'red'
if (newNode.parent.parent != root){
newNode.parent.parent.color = 'red'
}
}else (newNode.uncle = 'black'){ //获取uncle节点的方式有很多种
rotate(root) //参考上一篇文章
root.color = 'black' //这里的root是指当前子树的root,不是整棵树的root
root.left = root.right = 'red'
}
}
最坏情况
假设我们继续增加根节点的左子树,把这颗树增加到很高,有100层,从规则上分析:
最坏情况下,这颗红黑树可以全部是黑色,然后在root的左子树中,每个一层黑色节点增加一层红色,就可以保证红色节点的子节点都是黑色(规则4),理论上可以增加50层红色节点进去。
想象一下右子树不停的延伸,而左子树延伸时全部补黑色节点。
那么最坏情况下,两个子树的高度差会是 K/2(K为整颗树的高度),那么,这颗红黑树的搜索性能是不如AVL树的。
但是,因为红黑树在一半的情况下插入只需要修改颜色即可,而不需要进行旋转,如果树结构会经常变动,总的性能来说还是要强于AVL树。
删除
删除是红黑树操作里最复杂的部分,但是我们可以去仔细拆解这一过程:
和AVL树一样,我们可以将删除操作看成两个部分:
- 删除节点(参考【技术点】数据结构–二叉树(一))
- 平衡操作,AVL有AVL的操作,红黑树就按照红黑树的操作来。
在二叉树的删除操作中,我们分了三个场景。这里可以抽象一下,综合成一个场景:
删除某个节点后,这个节点是通过其后继节点来替代(场景三,使用右子树里最小的)。如果删除节点没有后继节点,我们就使用其前继节点(场景二,只有左子树)来替代,如果都没有,直接删除。
前继和后继节点的概念,我借用一张图来说明(引用自30张图带你彻底理解红黑树):
把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点。

所以,实际上我们把删除某个节点X,转换成了两个步骤。
也就是上述的步骤1可以拆分成两个步骤:
1.1. 找到后继或者前继节点P,并将该节点的值复制到删除节点上
1.2 删除后继或者前继节点P。
这里还隐藏了一个问题需要说明一下,可能有的同学就会说,删除后继或者前继节点会不会影响这个节点的子树?实际上,我们仔细想一下就可以确定两点:
- 前继节点没有右子树,不然这个右子树就更接近删除节点的值
- 后继节点没有左子树,不然这个左子树就更接近删除节点的值
所以删除的时候,按照删除逻辑里的有一颗或者无子树的逻辑删除即可,结构调整相对比较简单。
所以,接下来,我们就是要考虑一个问题,在前继或者后继节点删除了之后怎么平衡的问题。从规则来看,一般都是删除了节点从而破坏了规则4或者规则5。
我们可以从替代节点(后继或者前继)的颜色和位置信息来分析,列出若干种删除场景来:
先看下颜色:
-
场景1:替代节点为红色
替代节点去替代删除节点,相当于替代节点本身被删除,因为是红色节点,所以不会破坏替代节点原有位置的平衡,所以不需要考虑替代节点的位置信息了,我们就只需要将替代节点放置在删除节点之后,将原删除节点的颜色复制给替代节点即可。function deleteRedReplace(root, delNode){ p = find_next(root, delNode) delNode.value = p.value del(root, p) } -
场景二,替代节点为黑色,因为替代节点会被删除掉,从而破坏规则5(路径上的黑色节点数肯定会被破坏掉),因此需要考虑替代节点的位置信息了。
我们考察一下,删除节点会影响到哪些位置信息,假设删掉的节点为X,那么会影响到的就是子树(节点N)、兄弟节点(节点S与其两个子树:SL & SR)、父节点(节点P)的三中位置关系。
根据上文的几条假设:
2.1 X为黑色。
2.2 X为后继或者前继节点,只会存在一个子树。
再加上子树、兄弟节点、父节点可以是黑色或者红色,我们可以分成如下几种子场景 -
场景2.1 子树、兄弟节点、父节点均为黑色,
这种情况下,删掉X,会影响从X往其子树的路径,所有的经过X的路径全部要减1。此时,我们只需要将X的兄弟节点变色为红色即可。也就是说从兄弟节点这里过去的所有黑色节点全部减1就可以保持平衡了。
这里举的例子是X为前继 (从删除节点的左子树里面选出了替代节点X),如果X是后继,逻辑上是一样的。大家可以推理一下。

-
场景2.2 N为红色,其他均为黑色
这种情况下,删掉X,会影响从X往其子树的路径,所有的经过X的路径全部要减1。此时,我们只需要将X的兄弟节点变色为红色即可。也就是说从兄弟节点这里过去的所有黑色节点全部减1就可以保持平衡了。

也就是说N不管是黑是红,对操作没啥影响,都是把S改成红色。其实也很好理解,删除的是X,不管后面是红是黑,都需要减1。所以场景2.1和2.2可以合并。子树颜色可以不作为一个变量 -
场景2.3 S为红色,其他均为黑色
在X这条路径减1的情况下,已经无法靠变色来解决了,需要进行旋转:

可以从图中看出,做完一个RR旋转之后还是无法满足,从新的S出发的左子树多1,还需要做两个变色,S变成黑色,P变成红色。 -
场景2.4 父节点为红色在一般情况下,删除X不会有什么影响,知识在上述的2.3场景中,不需要对P进行变色了。但是代码实际上统一一份:
p.color = 'red' -
场景2.5 SL为红色
这种情况也是比较麻烦,直接上图:
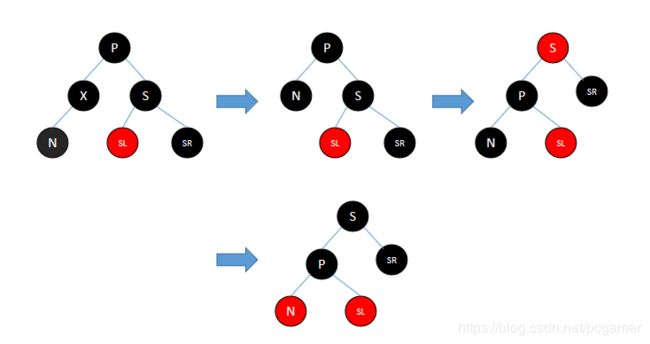
从图中可以看出,因为不知道SR的其他子树是什么状况,不能直接把SR改成红色,不然引入一个递归的判断就没法收敛了。所以只能在这个小区域中解决,先做一个RR旋转,然后再将N变为红色。 -
场景2.6 SR为红色
上图:
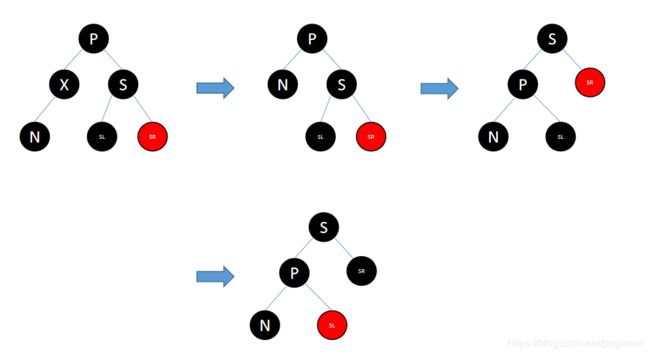
同样是一个RR旋转后,由于SL转成了P的有子树,导致原来的路径增加了1,所以SL需要变成红色,SR要变成黑色才能保持平衡。 -
场景2.7 SR与SL均为红色

和场景2.6类似,但是这里因为SL为红色,没有破坏原来左子树的平衡,所以之需要将SR变成黑色即可。 -
上述场景都是以X为前继节点来举例的,实际上后继节点是类似的,也是旋转之后变色,基本上就是上面几种场景的镜像,就不一一列举了。
总结
写红黑树比之前的二叉树和AVL树都困难得多,一是因为红黑树的结构确实复杂。二是红黑树给出的那几条规则只是一个指导性的规则。没有一个针对插入,特别是删除的一个很明确的指导性的操作。比如AVL的四中旋转方式,在某种情况下就采用某种旋转。
所以只能仔仔细细的一种一种场景推导及分析(删除节点的影响的环境变量分析得出场景),利用两种平衡操作(旋转 + 变色)对树进行平衡操作。
希望在文章中能把推导过程写清楚,让大家能看懂为什么有这么多的场景,每种场景又可以怎么去做。而不是直接丢出几种场景,那样不好理解和记忆。
好在是终于成文了,有不足和遗漏的地方欢迎补充,如有帮助请收藏。
下一步
二叉树的内容基本上是差不多了。下一步准备扩展一下,把其他的一些经典的树结构来讲一讲,比如B+树等。
敬请期待。
