极简的微积分
大学的微积分想必折磨了无数个像我一样的工科生。但是在微积分出世的那时,谁又能想到后来人仅凭一个电阻和一个电容便能实体化这些冷冰冰的公式!
没错,微分电路和积分电路都是只由一个电阻和一个电容所构成的,为什么这么简单的电路却能够实现微积分的运算?
微分电路
输出取自电阻两端电压,构成微分电路。以输入方波信号为例(未作特殊说明,本文默认输入都为上图的方波形式,峰值规定为1V),要使该电路能完美地实现微分,就要求时间常数$\tau = RC << t_p$,其中$t_p$是矩形脉冲宽度。由这个条件我们可以将电容电压$u_c(t)$近似为电源电压$u_s(t)$:
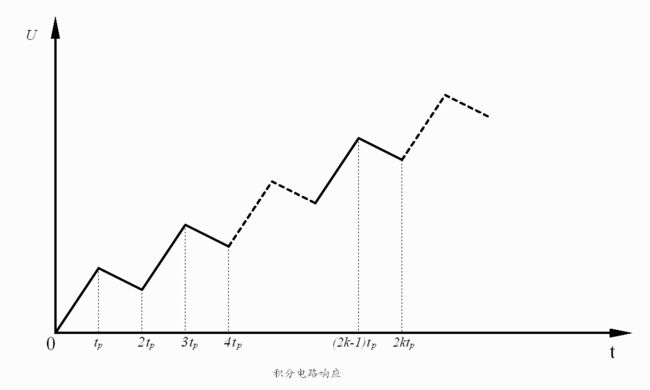
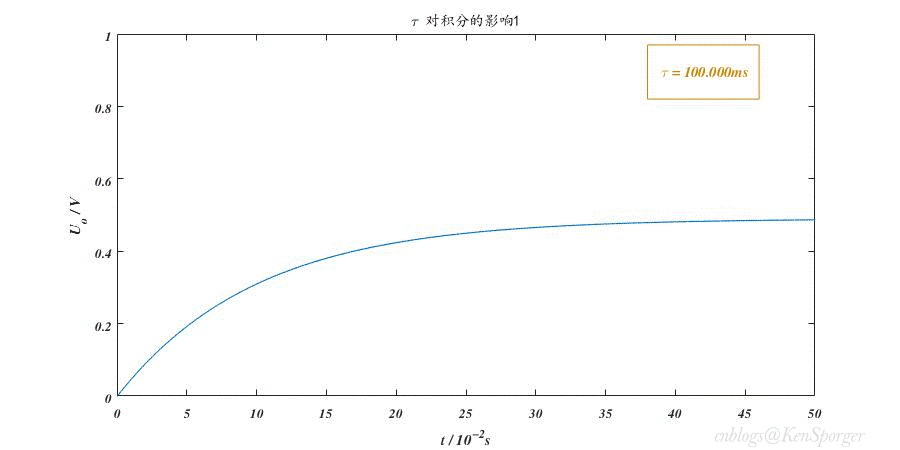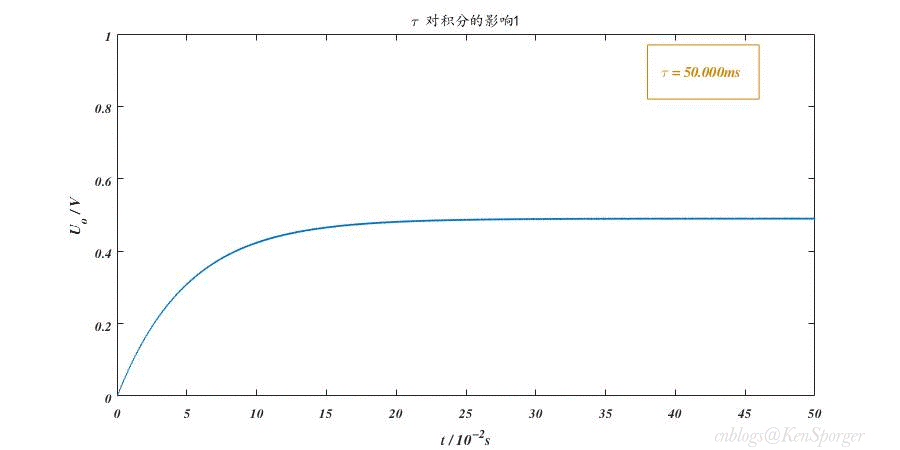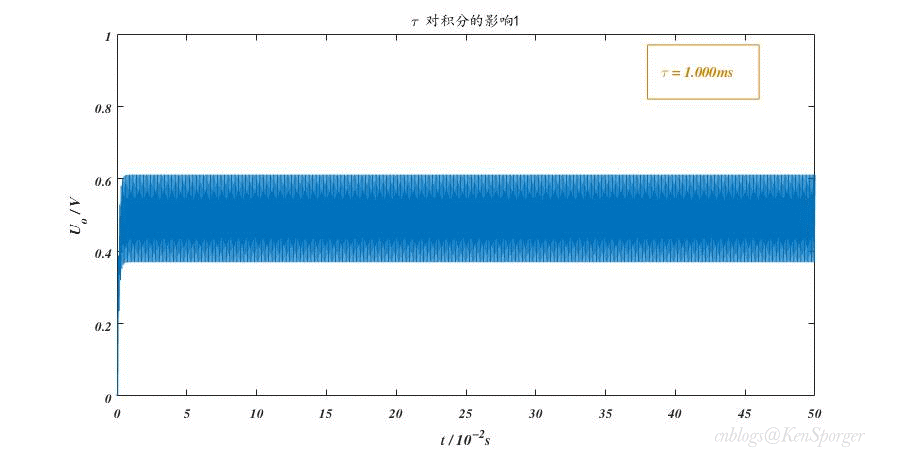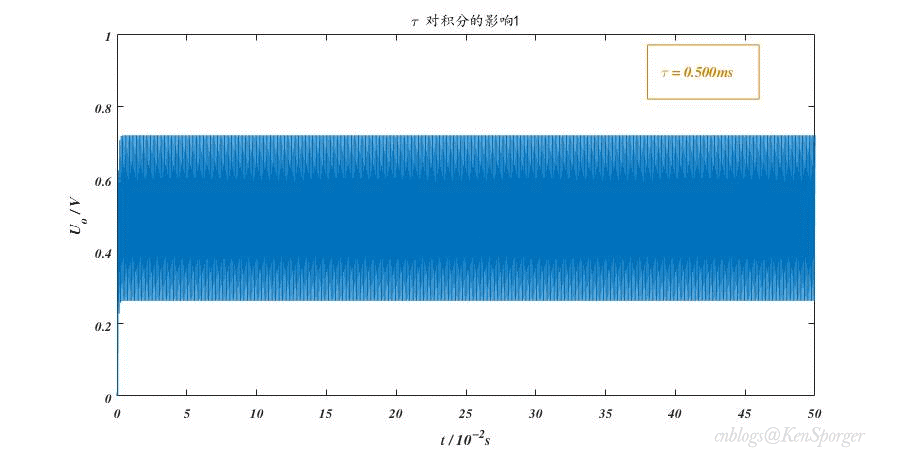
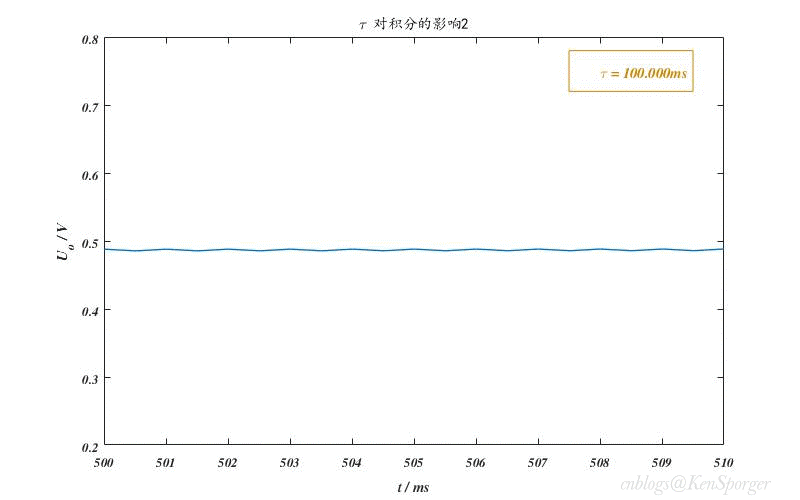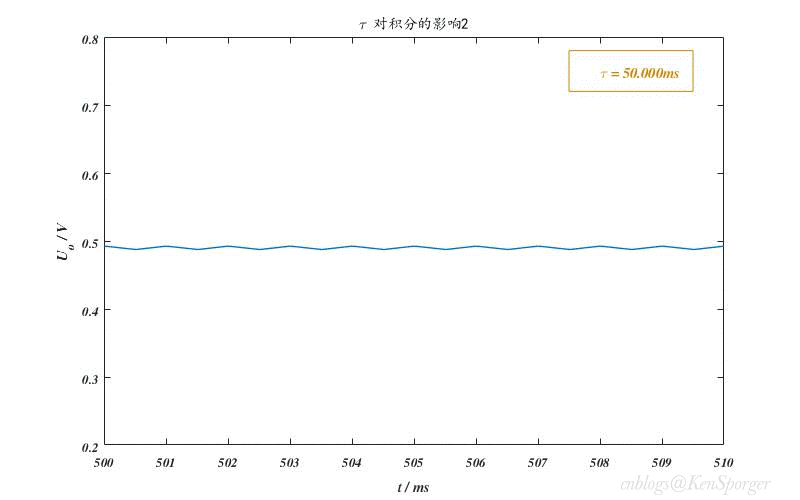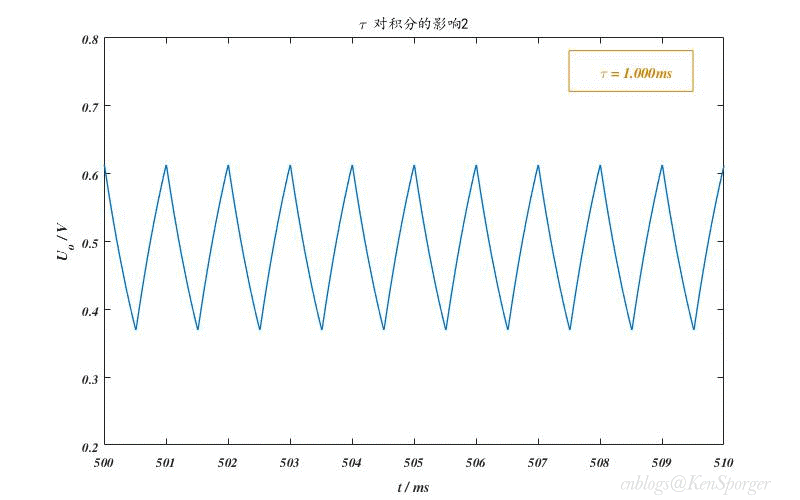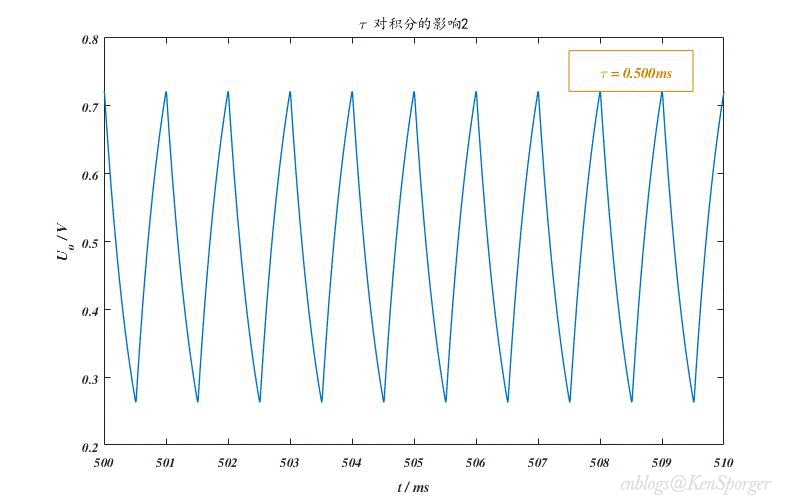
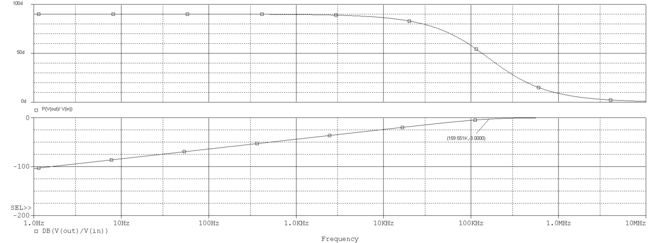
$RC< 周期化作角频率,可得$\frac{1}{\omega C} >> R$ 所以,$u_c(t) >> u_o(t)$,$u_c(t) \approx u_s(t)$ 假设电压初始状态$u_c(0_{\_})=0V$,结合电容的电压与电流关系,可得电路输出是输入电压的微分: $u_o(t)=i_cR=RC\frac{d{u_c(t)}}{dt} \approx \tau \frac{du_s(t)}{dt}$ 同样,积分电路也采用类似的分析方法。但不同于微分电路 ,时间常数$\tau = RC >> t_p$才能实现较好的积分效果。此时,$u_s(t) \approx u_R(t)$。 输出直接取自电容的电压,因此输出是输入电压的积分。 $u_o(t)=u_c(t)=\frac{1}{C}\int_{0}^{t} i_R(t) dt = \frac{1}{RC}\int_{0}^{t} u_R(t) dt \approx \frac{1}{\tau}\int_{0}^{t} U_s(t) dt$ 先以微分电路为例,分析各电压响应间的关系。在一开始,输入为0V,电容相当于短路,输出也为0V;当脉冲来临,输入跳变到1V,由于电容两端电压不能突变,所以$u_c=0V$,输出瞬间跳变为1V。此后,输入一直维持在1V,电容也开始慢慢充电,$u_c$逐渐上升,导致输出减小;直到输入跳变回0V,由于电容电压不能突变,仍然为1V,将输入视作接地,则$u_o=-u_c$,因为电容开始放电,因此输出也从-1V向0V增大。 积分电路的分析要更为复杂些。如上图,$(2k-2)t_p \sim (2k-1)t_p$间有电压输入,电容进行充电。由于时间常数较大,充电速度较慢,因此远没有达到饱和状态;$(2k-1)t_p \sim 2kt_p$间输入为零,电容进行放电,同样放电速度较慢。经过多个周期,电容两端的电压会累积得越来越多。更深入的,将用定量分析来表述。 电容元件在时域中的完全响应为$u_c(t)=u_c(\infty)+[u_c(0_+)-u_c(\infty)] e^{-\frac{t}{\tau}}$。假设电压初始状态$u_c(0_{\_})=0V$,则零状态响应为$u_c(t)=u_c(\infty)-u_c(\infty) e^{-\frac{t}{\tau}}$,$u_c(\infty)$在这里就是电容充满电后的电压,即等于脉冲的峰值电压;假设外施激励为零,则零输入响应为$u_c(t)=u_c(0_{\_}) e^{-\frac{t}{\tau}}$。 对于微分电路而言,矩形脉冲期间可以视作零状态响应,$u_c(t)=(1- e^{-\frac{t}{\tau}})V$,则$u_o(t)=e^{-\frac{t}{\tau}} V$;零激励期间可以视作零输入响应,$u_c(t)=e^{-\frac{t}{\tau}}V$,$u_o(t)=-e^{-\frac{t}{\tau}}V$ 。并且,只要在每个期间内,电容能完全地充放电,那么每个周期的响应之间都是彼此独立且相同的。 (敲黑板,重点来了) 而积分电路中,$(2k-1)t_p \sim 2kt_p$段可以视作零输入响应,其初始状态为$u_c(0_{\_})=u_c((2k-1)t_p)$;$(2k-2)t_p \sim (2k-1)t_p$段既有初始状态,又有外加激励,因此是完全响应,可以分解成零状态响应+零输入响应进行求解。 我们先考察一下开始几个点的响应,为了表示的方便,记$e^{-\frac{t_p}{\tau}}=W$,$U(k)=u_c(kt_p)$,再次说明输入峰值为1V: $U(1)=1-W^1=W^0-W^1$ $U(2)=U(1)·W^1=W^1-W^2$ $U(3)=U(2)·W^1 + 1-W^1=W^0+W^2-(W^1+W^3)$ 不难推断: $U(2k-1)=\sum_{i=0}^{k-1}(W^{2i}-W^{2i+1}),k=1,2,3···$ $U(2k)=U(2k-1)·W^1=\sum_{i=1}^{k}(W^{2i-1}-W^{2i}),k=1,2,3···$ 定义中心电压:$U_0(k)=\frac{2U(k)+U(k-1)+U(k+1)}{4}=\frac{2-W^{k}-W^{k+1}}{4},k=0,1,2,3···$ 前两个式子都是等比数列的和,公比为$W^2$,因为$0 下图是R=10k,C=10uF时积分电路的响应变化情况。 如果输入的峰值变为$E$,那么最终积分电路的稳态输出为$\frac{1}{2}E$,也就是说积分电路对输入具有取均值的功能。从上述分析中,也能看出,积分电路并非真正的积分,其原因就在于零激励时电容存在放电,无法维持电压不变。 前面我们讲过,微分电路的时间常数较小,积分电路的时间常数较大。这样规定是因为在这里,时间常数是衡量电容充放电速度的一项指标,而电容充放电的快慢则影响了微积分的效果。 我们知道,在$t=0$时刻,电容刚开始要充电,两端电压还是0V;随着时间的推移,电容电压越来越接近脉冲峰值,直到电源由脉冲变为0V,之后便开始放电归零。显然,如果$\tau$越小,充放电速度就越快,达到峰值或者归零所用的时间就越短,这显然适用于微分电路。而$\tau$较大时,充放电较慢,不容易达到饱和,所以适合积分电路。 以微分为例,上图展示了$\tau$值变化对输出波形的影响。$\tau$较大时候,电容充放电的时间远大于$t_p$,所以当输入发生跳变时,电容电压甚至还没有放完电或者是充满电;随着$\tau$值减小,输出波形越来越接近冲激(理想的微分输出)。 也许有人会说,为了波形越接近冲激,那让$\tau$取得极限小不是很好嘛。这其实是有问题的——从图中可以发现,$\tau$太小时,输出波形的幅值也会减小。至于变小的原因,可以理解为电容状态改变得很快,其波形几乎和输入电压的波形重合,导致在跳变瞬间电阻的分压非常小(或者从1.1节中的结论公式入手)。另外,注意到$\tau$过大时,输出幅值也会减小,这是因为电容来不及充放电所导致的。例如,输入从0V跳变至1V时,电容由于之前还未放完电,导致现在两端电压$u_c>0V$,这就造成输出$u_o<1V$。因此实际应用中,应该选择一个较为合适的时间常数。 回忆上文推导过的公式,时间常数决定了W的大小,而W又决定了电路以下几个特性:稳态峰峰值、过渡时间(达到稳态所需的时间)和电容状态(是否会饱和)。 但是,只要$0 第一,稳态峰峰值之前已经算过,是$\frac{1-W}{1+W}$。当$\tau$增大,则$W$变大,峰峰值减小。 第二,根据中心电压$U_0(k)=\frac{2-W^{k}-W^{k+1}}{4}$,当$\tau$增大,则$W$变大,那么中心电压收敛的时间就会变长(过渡时间变长)。 第三,当$\tau$减小时,电容充放电的速度会变快,甚至导致饱和状态的出现,失去积分功能。 先分析微分电路的频率特性: $F=\frac{U_{o}(j\omega)}{U_{s}(j\omega)}=\frac{R}{R+\frac{1}{j\omega C}}$ 令$\omega _c = \frac{1}{RC}$,则$F=\frac{1}{1-j\frac{\omega_c}{\omega}}$ 幅频特性:$|F|=\frac{1}{\sqrt{1+(\frac{\omega_c}{\omega})^2}}$ 相频特性:$\phi = arctan\frac{\omega_c}{\omega}$ 当$\omega \rightarrow 0$时,$|F|=0$,$\phi = 90^{\circ}$; 当$\omega \rightarrow \omega_c$时,$|F|=\frac{\sqrt{2}}{2}$,$\phi =45^{\circ}$; 当$\omega \rightarrow \infty$时,$|F|=1$,$\phi = 0^{\circ}$; 由上述可知,微分电路具有高通特性,并且输出超前于输入信号。将$ \omega_c$定义为RC微分电路的截止角频率。 下图是不同频率正弦波激励下的相频曲线和幅频曲线(输入正弦波,输出也为正弦波)。 用相同的方法,我们可以得到: $F=\frac{1}{1+j\frac{\omega}{\omega_c}}$ 其特性与微分电路恰好相反——低通、输出滞后。$ \omega_c$定义为RC积分电路的截止角频率。 感谢以下前辈文章对我的帮助: 闫俊荣,黄艳《RC电路的特性分析及应用》; 胡斌《积分和微分电路分析方法》; 李彩萍,李乐生《方波激励下一阶RC电路响应的研究》; 吕伟峰《RC积分微分电路实验的误差分析方法》; 积分电路
响应分析
定性分析
定量分析
时间常数的意义
对微分的影响
对积分的影响
频率特性
微分高通
积分低通
参考文献