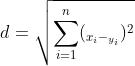K最近邻算法(KNN)
K最近邻 (k-Nearest Neighbors,KNN) 算法是一种分类算法,也是最简单易懂的机器学习算法,没有之一。1968年由 Cover 和 Hart 提出,应用场景有字符识别、文本分类、图像识别等领域。该算法的思想是:一个样本与数据集中的k个样本最相似,如果这k个样本中的大多数属于某一个类别,则该样本也属于这个类别。还是直接讲例子最好懂,一直没找到好的例子,就改造了下Peter Harrington的《机器学习实战》中电影分类的例子,当然实际情况不可能这么简单,这里只是为了说明该算法的用法。
先准备下电影分类数据集(电影名称与分类来自于优酷网;镜头数量则纯属虚构):
| 序号 |
电影名称 |
搞笑镜头 |
拥抱镜头 |
打斗镜头 |
电影类型 |
| 1. |
宝贝当家 |
45 |
2 |
9 |
喜剧片 |
| 2. |
美人鱼 |
21 |
17 |
5 |
喜剧片 |
| 3. |
澳门风云3 |
54 |
9 |
11 |
喜剧片 |
| 4. |
功夫熊猫3 |
39 |
0 |
31 |
喜剧片 |
| 5. |
谍影重重 |
5 |
2 |
57 |
动作片 |
| 6. |
叶问3 |
3 |
2 |
65 |
动作片 |
| 7. |
伦敦陷落 |
2 |
3 |
55 |
动作片 |
| 8. |
我的特工爷爷 |
6 |
4 |
21 |
动作片 |
| 9. |
奔爱 |
7 |
46 |
4 |
爱情片 |
| 10. |
夜孔雀 |
9 |
39 |
8 |
爱情片 |
| 11. |
代理情人 |
9 |
38 |
2 |
爱情片 |
| 12. |
新步步惊心 |
8 |
34 |
17 |
爱情片 |
| 13. |
唐人街探案 |
23 |
3 |
17 |
? |
上面数据集中序号1-12为已知的电影分类,分为喜剧片、动作片、爱情片三个种类,使用的特征值分别为搞笑镜头、打斗镜头、拥抱镜头的数量。那么来了一部新电影《唐人街探案》,它属于上述3个电影分类中的哪个类型?用KNN是怎么做的呢?
首先,我们构建一个已分好类的数据集。
对于一个规模巨大的数据集,显然数据库是更好的选择。这里为了方便验证,使用Python的字典dict构造数据集。
movie_data = {"宝贝当家": [45, 2, 9, "喜剧片"],
"美人鱼": [21, 17, 5, "喜剧片"],
"澳门风云3": [54, 9, 11, "喜剧片"],
"功夫熊猫3": [39, 0, 31, "喜剧片"],
"谍影重重": [5, 2, 57, "动作片"],
"叶问3": [3, 2, 65, "动作片"],
"伦敦陷落": [2, 3, 55, "动作片"],
"我的特工爷爷": [6, 4, 21, "动作片"],
"奔爱": [7, 46, 4, "爱情片"],
"夜孔雀": [9, 39, 8, "爱情片"],
"代理情人": [9, 38, 2, "爱情片"],
"新步步惊心": [8, 34, 17, "爱情片"]}第二步:计算一个新样本与数据集中所有数据的距离。
这里的新样本就是:"唐人街探案": [23, 3, 17, "?片"]。欧式距离是一个非常简单又最常用的距离计算方法。
其中x,y为2个样本,n为维度,xi,yi为x,y第i个维度上的特征值。如x为:"唐人街探案": [23, 3, 17, "?片"],y为:"伦敦陷落": [2, 3, 55, "动作片"],则两者之间的距离为:![]() =43.42。
=43.42。
下面为求与数据集中所有数据的距离代码:
x = [23, 3, 17]
KNN = []
for key, v in movie_data.items():
d = math.sqrt((x[0] - v[0]) ** 2 + (x[1] - v[1]) ** 2 + (x[2] - v[2]) ** 2)
KNN.append([key, round(d, 2)])
print(KNN)输出结果:
[['谍影重重', 43.87], ['伦敦陷落', 43.42], ['澳门风云3', 32.14], ['叶问3', 52.01], ['我的特工爷爷', 17.49], ['新步步惊心', 34.44], ['宝贝当家', 23.43], ['功夫熊猫3', 21.47], ['奔爱', 47.69], ['美人鱼', 18.55], ['夜孔雀', 39.66], ['代理情人', 40.57]]第三步:按照距离大小进行递增排序。
KNN.sort(key=lambda dis: dis[1])输出结果:
[['我的特工爷爷', 17.49], ['美人鱼', 18.55], ['功夫熊猫3', 21.47], ['宝贝当家', 23.43], ['澳门风云3', 32.14], ['新步步惊心', 34.44], ['夜孔雀', 39.66], ['代理情人', 40.57], ['伦敦陷落', 43.42], ['谍影重重', 43.87], ['奔爱', 47.69], ['叶问3', 52.01]]第四步:选取距离最小的k个样本。
这里取k=5;
KNN=KNN[:5]输出:[['我的特工爷爷', 17.49], ['美人鱼', 18.55], ['功夫熊猫3', 21.47], ['宝贝当家', 23.43], ['澳门风云3', 32.14]]
第五步:确定前k个样本所在类别出现的频率,并输出出现频率最高的类别。
labels = {"喜剧片":0,"动作片":0,"爱情片":0}
for sin KNN:
label = movie_data[s[0]]
labels[label[3]] += 1
labels =sorted(labels.items(),key=lambdal: l[1],reverse=True)
print(labels,labels[0][0],sep='\n')[('喜剧片', 4), ('动作片', 1), ('爱情片', 0)]
喜剧片
KNN有几个特点:
(1)KNN属于惰性学习(lazy-learning)
这是与急切学习(eager learning)相对应的,因为KNN没有显式的学习过程!也就是说没有训练阶段,从上面的例子就可以看出,数据集事先已有了分类和特征值,待收到新样本后直接进行处理。
(2)KNN的计算复杂度较高
我们从上面的例子可以看到,新样本需要与数据集中每个数据进行距离计算,计算复杂度和数据集中的数据数目n成正比,也就是说,KNN的时间复杂度为O(n),因此KNN一般适用于样本数较少的数据集。
(3)k取不同值时,分类结果可能会有显著不同。
上例中,如果k取值为k=1,那么分类就是动作片,而不是喜剧片。一般k的取值不超过20,上限是n的开方。